Jenis Bahagian Konikal, Aplikasi, Contoh

The Bahagian konik Mereka adalah lengkung yang diperoleh dengan memintas satah dengan kerucut. Terdapat beberapa cara untuk melakukan ini; Contohnya, jika satah diluluskan secara serentak ke paksi paksi kon yang diperolehi.

Memandang satah sedikit berkenaan dengan paksi paksi kerucut, elips diperolehi, lengkung yang ditutup, tetapi jika kita merendahkannya lebih banyak parabola atau hiperbola diperolehi, seperti yang dapat dilihat dalam animasi Rajah 1.

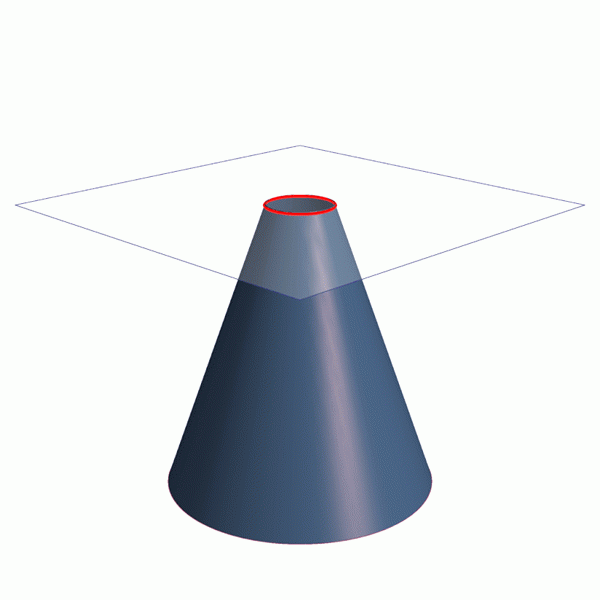Animasi yang menunjukkan cara mendapatkan empat bahagian kerucut: lilitan, perumpamaan dan hiperbola elips. Sumber: Wikimedia Commons. Garis / cc0

Bahagian kerucut adalah sebahagian daripada sifat dan dunia di sekeliling kita. Kejuruteraan, Senibina dan Astronomi adalah cabang pengetahuan penting yang membuat kegunaan conics.

[TOC]

Syarat untuk bahagian kerucut

Bahagian kerucut ditakrifkan sebagai tempat geometri yang memenuhi syarat -syarat berikut:

Perumpamaan

Ini adalah tempat geometri dari semua titik yang terletak di satah yang sama ke titik tetap yang dipanggil Fokus F dan garis lurus juga tetap, dipanggil arahan.

Ellipse

Titik kapal terbang tergolong dalam elips jika jumlah jarak antara titik itu dan dua titik tetap lain, yang dipanggil Focos dan terletak di paksi utama elips, tetap berterusan.

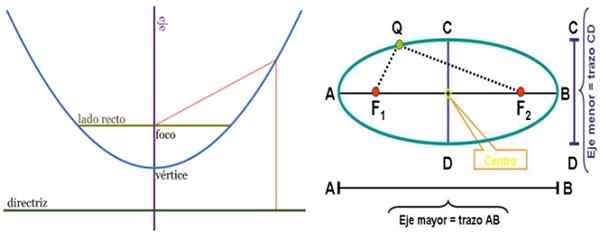Perumpamaan ke kiri dan elips ke kanan, dengan elemen masing -masing. Foci adalah mata dengan banyak aplikasi. Sumber: Wikimedia Commons.

Lilitan

Ia adalah tempat geometri semua mata yang mengekalkan jarak yang sama ke titik lain yang dipanggil Centro. Jarak ini adalah radio dari lilitan.

Boleh melayani anda: Jarak Euclidian: Konsep, Formula, Pengiraan, Contoh

Hyperbola

Set mata dalam satah supaya perbezaan antara jaraknya ke dua titik tetap yang dipanggil Focos, ia tetap.

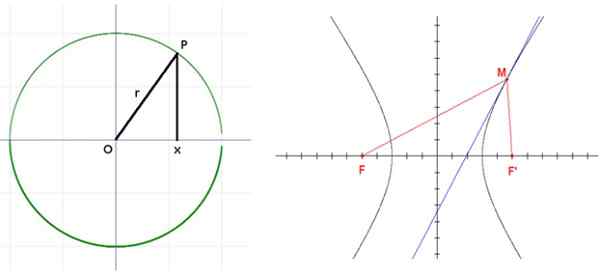Hyperbola dengan foci f dan f. Sumber: Wikimedia Commons.

Aplikasi

Mari lihat beberapa aplikasi bahagian kerucut:

Perumpamaan  

-Apabila objek dilancarkan, trajektori yang berikut mempunyai bentuk perumpamaan.

-Perumpamaan mempunyai aplikasi kejuruteraan yang ketara, contohnya dalam jambatan yang digantung, kabel tergesa -gesa dalam bentuk perumpamaan.

-Perumpamaan juga baik untuk membuat reflektor dan teleskop. Ini adalah terima kasih kepada harta yang menarik: Semasa meletakkan luminaire dalam fokus permukaan seksyen melintang parabola, cahaya akan bergerak dalam sinar selari ke paksi perumpamaan.

-Jika sinar bercahaya selari dengan paksi simetri mendekati permukaan parabola, ia menumpukan mereka dalam fokus, keadaan yang digunakan untuk membuat teleskop reflektor, seperti teleskop Hale de Monte Palomar.

Ellipses

-Planet -planet sistem suria bergerak berikutan trajektori elips, agak dekat dengan lilitan dalam hal planet utama, tanah termasuk. Matahari tidak berada di tengah, tetapi di salah satu lampu sorot.

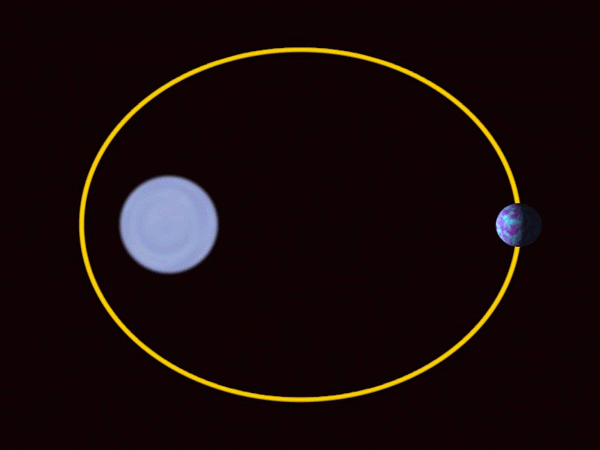Planet sistem suria bergerak di orbit elips dengan matahari di salah satu lampu sorot. Sumber: Wikimedia Commons.

-Ellipse digunakan secara meluas dalam seni bina sebagai elemen hiasan dan reka bentuk.

-Dengan meletakkan reflektor dalam salah satu lampu sorot elips, cahaya dicerminkan ke arah fokus yang lain. Perkara yang sama berlaku dengan bunyi. Itulah sebabnya di dewan -dewan berbentuk Ellipse, yang bercakap secara senyap -senyap terletak dalam satu tumpuan jelas didengar oleh pendengar yang terletak di fokus yang lain.

Ia dapat melayani anda: prisma hepagon

-Harta yang sama ini mempunyai aplikasi yang mengejutkan dalam bidang perubatan. Pengiraan buah pinggang dapat dimusnahkan dengan suara. Gelombang ultrasound intensiti yang hebat dihasilkan di salah satu tumpuan tab elips yang penuh dengan air, dan pesakit terletak di fokus yang lain. Gelombang bunyi mempengaruhi dan mencerminkan pengiraan, dan dengan tenaga mereka, mereka memisahkannya dalam kepingan kecil, yang mana orang itu kemudiannya mudah dikeluarkan semasa membuang air kecil.

Hyperbolas

-Beberapa komet dalam sistem solar mengikuti trajektori hiperbola, selalu dengan matahari di salah satu foci.

-Fokus hiperbola juga sangat menarik untuk mengkaji fenomena refleksi gelombang. Sebagai contoh, dengan mengarahkan sinar cahaya kepada tumpuan cermin parabola, ia ditunjukkan dalam fokus yang lain, harta yang sangat berguna untuk membina teleskop, kerana cahaya dapat memberi tumpuan kepada cermin parabola dan diarahkan ke tempat lain yang lebih sesuai mengikut reka bentuk.

-Menara penyejuk loji nuklear mempunyai siluet berbentuk hiperbola.

-Sebelum kedatangan GPS, hiperbola digunakan dalam navigasi untuk mencari bot. Kapal yang dibawa pada isyarat papan yang dikeluarkan secara serentak oleh stesen radio A dan B dan komputer bertanggungjawab untuk mendaftarkan perbezaan masa ketibaan isyarat, untuk mengubahnya menjadi perbezaan jarak jauh. Dengan cara ini kapal terletak di cawangan hiperbola.

Prosedur ini diulang dengan dua stesen radio C dan D yang lain, yang meletakkan kapal di cawangan Hyperbola lain. Kedudukan muktamad bot adalah persimpangan kedua -dua hiperbola.

Boleh melayani anda: Fungsi Berkembang: Cara Mengenalpasti, Contoh, Latihan

Lingkaran

-Ketibaan roda mengubah perjalanan sejarah.

-Pergerakan bulat sangat biasa, banyak kepingan berputar untuk menghasilkan pelbagai kesan, dari kilang ke peminat.

-Walaupun trajektori planet utama adalah elips, trajektori bulat adalah pendekatan yang baik dalam banyak kes.

-Circunferences adalah unsur kerap dalam seni bina, reka bentuk, kejuruteraan dan pembinaan. Senarai bentuk bulat atau cakera tidak berkesudahan: duit syiling, CD, jam tangan dan banyak lagi.

Contoh

Kemudian terdapat dua conics dalam pesawat, bulatan dan elips.

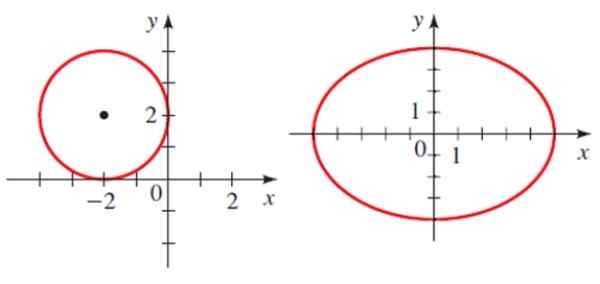Contoh bahagian kerucut: bulatan dan elips. Sumber: Stewart, J. Precalculation.

Setiap mempunyai persamaan analisis:

Lilitan

(X-h)² + (Y-K)² = R²

Di mana h dan k adalah koordinat pusat dan r adalah radio. Untuk lilitan yang ditunjukkan dalam angka persamaan adalah:

(x+2)² + (Y-2)² = 4

Ellipse

Persamaan elips yang pusatnya adalah titik koordinat (h, k):

[(X-h)² /ke² ]+ [(y-k)² /b² ] = 1

Di mana a dan b adalah separuh daripada elips. Untuk elips yang ditunjukkan, pusat berada pada titik 0.0, separuh terbesar yang sama adalah sama dan separuh kecil adalah 4. Oleh itu persamaannya adalah:

(x² /25)+ (dan² / 16) = 1

Rujukan

1. Hoffman, J. Pemilihan masalah matematik. Jilid 2.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
4. Wikipedia. Seksyen conic. Pulih dari: Adakah.Wikipedia.org.
5. Zill, d. 1984. Algebra dan trigonometri. McGraw Hill.