Separuh bulatan cara mengira perimeter, kawasan, centroid, latihan

Dia separuh bulatan Ia adalah angka rata yang dibatasi oleh diameter lilitan dan salah satu daripada dua gerbang bulat rata yang ditentukan oleh diameter tersebut.

Dengan cara ini, separuh bulatan bersempadan dengan semikit, yang terdiri daripada arka bulat rata dan segmen lurus yang menyertai hujung arka bulat rata. Separuh bulatan meliputi separuh bulatan dan semua titik pedalaman yang sama.

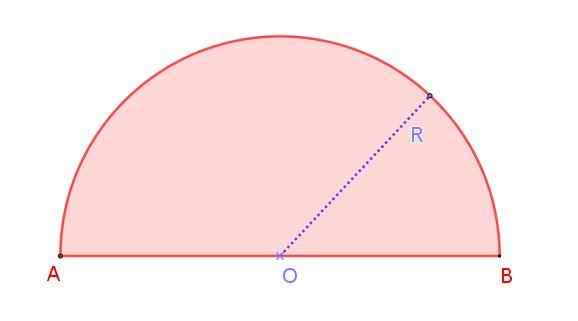Rajah 1. Radio R radio separuh bulatan. Sumber: f. Zapata.

Kita dapat melihat ini dalam Rajah 1, yang menunjukkan radio r rión r, yang mengukurnya separuh daripada diameter ab. Perhatikan bahawa tidak seperti bulatan, di mana terdapat diameter tak terbatas, di separuh bulatan hanya ada satu diameter.

Secircle bulatan adalah angka geometri dengan banyak kegunaan dalam seni bina dan reka bentuk, seperti yang kita lihat dalam imej berikut:

Rajah 2. Seminicírculo sebagai elemen hiasan dalam seni bina. Sumber: Pikist.

[TOC]

Unsur dan ukuran separuh bulatan

Unsur -unsur separuh bulatan adalah:

1.- Arka bulat rata a⌒b

2.- Segmen [ab] 

3.- Titik pedalaman ke separuh bulatan terdiri daripada arka dan segmen A⌒B [AB].

Perimeter separuh bulatan

Perimeter adalah jumlah kontur gerbang ditambah dengan segmen lurus, oleh itu:

Perimeter = panjang arka a⌒b + panjang segmen [ab]

Dalam hal radio separuh bulatan r perimeternya akan diberikan oleh formula:

P = π ⋅ r + 2 ⋅ r = (π + 2) ⋅ r

Istilah pertama adalah separuh daripada perimeter lingkaran radius, manakala yang kedua adalah panjang diameter, iaitu dua kali jejari.

Boleh melayani anda: skala termometrik

Kawasan separuh bulatan

Sebagai separuh bulatan adalah salah satu sektor sudut rata yang kekal dengan melukis diameter melalui lilitan, kawasannya akan separuh daripada kawasan bulatan yang mengandungi separuh bulatan radio r:

A = (π πr²) / 2 = ½ π ⋅²

Centroid dari separuh bulatan

Centroid dari separuh bulatan adalah pada paksi simetri ke ketinggian yang diukur dari diameternya 4/(3π) kali jejari r r.

Ini sepadan dengan kira -kira 0.424 ⋅ r, diukur dari pusat separuh bulatan dan pada paksi simetrinya, seperti yang ditunjukkan dalam Rajah 3.

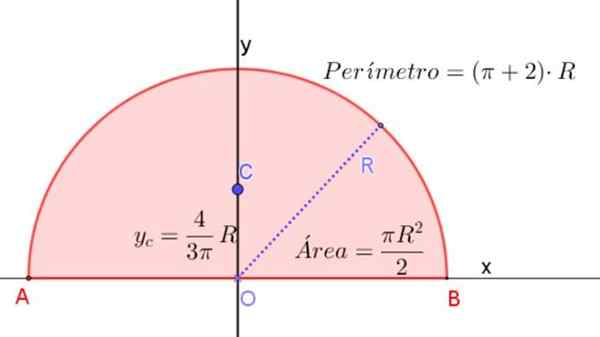Rajah 3. Separuh bulatan radio r, yang menunjukkan formula untuk menentukan kawasan, perimeter dan lokasi centroidnya. Sumber: f. Zapata.

Momen inersia separuh bulatan

Momen inersia angka rata ditakrifkan berkenaan dengan paksi, contohnya paksi x, seperti:

Integral segi empat jarak titik -titik yang dimiliki oleh angka ke paksi, perbezaan integrasi menjadi kawasan yang sangat kecil di kawasan, yang diambil dalam kedudukan setiap titik. 

Rajah 4 menunjukkan definisi momen inersia i_x dari separuh bulatan Radio R, berkenaan dengan paksi x yang melalui pepenjuru:

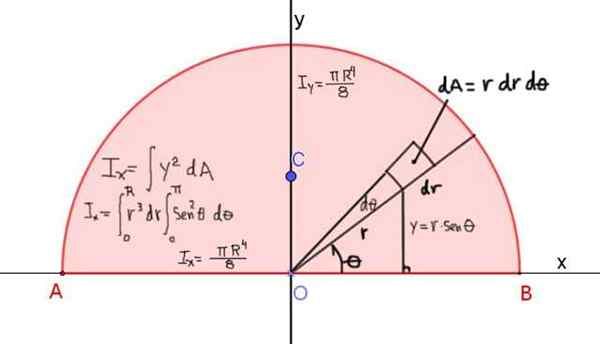Rajah 4. Definisi momen inersia IX dari separuh bulatan berkenaan dengan paksi x yang melalui pepenjuru. Hasilnya ditunjukkan untuk momen inersia berkenaan dengan paksi x dan y. Sumber: f. Zapata.

Momen inersia berkenaan dengan paksi x diberikan oleh:

Yo_x = (π ⋅⁴) / 8

Dan momen inersia berkenaan dengan paksi simetri dan:

Boleh melayani anda: optik bergelora

Iy = (π ⋅R⁴) / 8

Ia menunjukkan bahawa kedua -dua momen inersia bertepatan dengan formula mereka, tetapi penting untuk menekankan bahawa mereka dirujuk ke paksi yang berbeza.

Sudut berdaftar

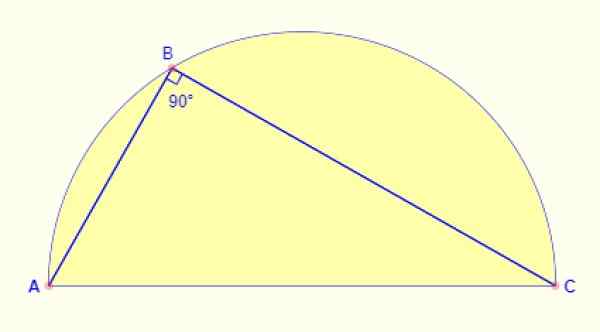
Sudut yang didaftarkan di separuh bulatan selalu 90º. Tidak kira mana bahagian gerbang dibawa ke titik, sudut yang terbentuk di antara sisi AB dan BC angka itu selalu lurus.

Rajah 5. Sudut didaftarkan di separuh bulatan. Sumber: Rujukan Terbuka Matematik.

Latihan yang diselesaikan

Latihan 1 

Tentukan perimeter separuh bulatan radius 10 cm.

Penyelesaian

Ingatlah bahawa perimeter bergantung kepada jejari diberikan oleh formula yang kita lihat sebelumnya:

P = (2 + π) ⋅ r

P = (2 + 3.14) ⋅ 10 cm = 5.14 ⋅ 10 cm = 51.4 cm.

Latihan 2

Cari kawasan separuh bulatan radio 10 cm.

Penyelesaian

Formula untuk kawasan separuh bulatan adalah:

A = ½ π ⋅r² = ½ π ⋅ (10cm)² = 50π cm² = 50 x 3.14 cm² = 157 cm².

Latihan 3

Tentukan ketinggian h dari centroid radius separuh bulatan r = 10 cm diukur dari pangkalannya, sama dengan diameter separuh bulatan. 

Penyelesaian

Centroid adalah titik keseimbangan separuh bulatan dan kedudukannya adalah pada paksi simetri pada ketinggian h asas (diameter separuh bulatan):

H = (4 ⋅ r) / (3π) = (4 ⋅10 cm) / (3 x 3.14) = 4,246 cm

Latihan 4

Cari momen inersia separuh bulatan berkenaan dengan paksi yang bertepatan dengan diameternya, mengetahui bahawa separuh bulatan diperbuat daripada lembaran nipis. Jejarinya adalah 10 cm dan jisimnya adalah 100 gram.

Penyelesaian

Formula yang memberikan momen inersia separuh bulatan adalah:

Boleh melayani anda: Fizik Negeri Pepejal: sifat, struktur, contoh

Yo_x = (π ⋅⁴) / 8

Tetapi sebagai masalah memberitahu kita bahawa ia adalah separuh bulatan material, maka hubungan sebelumnya mesti didarabkan oleh ketumpatan permukaan massa separuh bulatan, yang akan dilambangkan oleh σ.

Yo_x = σ (π πR⁴) / 8

Kami kemudian menentukan σ, yang tidak lain selain jisim separuh bulatan dibahagikan antara kawasan yang sama.

Kawasan ini ditentukan dalam Latihan 2 dan hasilnya ialah 157 cm². Kemudian ketumpatan dangkal separuh bulatan ini akan menjadi:

σ = 100 gram / 157 cm² = 0.637 g/cm²

Kemudian momen inersia berkenaan dengan diameter akan dikira seperti berikut:

Yo_x = (0.637 g/cm²) [3,1416 ⋅ (10cm)⁴]/ 8

Hasil:

Yo_x = 2502 g ⋅ cm²

Latihan 5

Tentukan momen inersia radius separuh bulatan 10 cm dibina dari lembaran bahan dengan ketumpatan permukaan 0.637 g/cm² oleh paksi yang melalui centroidnya dan selari dengan diameternya.

Penyelesaian

Untuk menyelesaikan latihan ini, perlu mengingati teorem Steiner pada saat -saat inersia paksi selari, yang mengatakan:

Momen inersia saya berkenaan dengan paksi yang berada pada jarak h dari centroid adalah sama dengan jumlah momen inersia i_c Mengenai paksi yang melewati centroid dan selari dengan yang pertama lagi produk doh melalui kuadrat pemisahan kedua -dua paksi.

I = i_c + M h²

Dalam kes kita, diketahui bahawa ia adalah momen inersia berkenaan dengan diameter, yang telah dikira dalam Latihan 4. H juga tahu antara diameter dan centroid, yang dikira dalam Latihan 3.

Kita hanya perlu membersihkan IC:

Yo_c = I - m h²

Yo_c = 2502 g ⋅ cm² - 100g ⋅ (4,246 cm)² mengakibatkan masa inersia dengan paksi selari dengan diameter dan yang melalui centroid adalah: 

Yo_c = 699.15 g ⋅ cm²

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Rujukan terbuka matematik. Separuh bulatan. Pulih dari: Mathpenref.com.
3. Formula Universe.Separuh bulatan. Pulih dari: universoformulas.com.
4. Formula Universe. Kawasan separuh bulatan. Pulih dari: universoformulas.com.
5. Wikipedia. Separuh bulatan. Diperoleh dari: dalam.Wikipedia.com.