Sifat siri Fibonacci, hubungan semula jadi, aplikasi

The O Siri Penggantian Fibonacci adalah urutan nombor yang diperolehi dengan permulaan dengan 0 dan 1, diteruskan dengan jumlah mereka: 0 + 1 = 1, maka jumlah sebelumnya: 1 + 1 = 2 dan sebagainya.

Mengikuti prosedur ini istilah lain diperoleh, mari kita lihat: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13 ..

Nombor pertama siri Fibonacci

Prosedur ini diulang seberapa banyak yang anda mahukan. Dengan cara ini, penggantian Fibonacci memperoleh bentuk: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Nombor yang membuatnya dipanggil Nombor Fibonacci.

[TOC]

Sejarah

Penggantian Fibonacci dipanggil seorang ahli matematik Itali yang tinggal di Zaman Pertengahan: Leonardo de Pisa, juga dikenali sebagai Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo menghabiskan masa kecil di Afrika Utara dan mengembara ke seluruh Mediterranean, di mana dia tahu sistem penomboran Indo -Arab dan gembira dengannya. Mungkin guru Arab Leonardo mengajarnya tentang penggantian, yang sudah dikenali oleh ahli matematik Hindu.

Seterusnya, ketika kembali ke Pisa Fibonacci menulis sebuah buku yang dipanggil Liber Abaci (The Book of Abacus), di mana sebagai tambahan untuk menonjolkan kelebihan nombor Indo -Arab dalam menghadapi penomboran Rom dan memperkenalkan 0, dia menimbulkan masalah mengenai pembiakan arnab.

Dan penyelesaian kepada masalah ini adalah tepat bilangan penggantian Fibonacci.

Leonardo de Pisa tidak dianugerahkan penciptaan penggantian; Dia hanya menyebutnya dalam bukunya sebagai rasa ingin tahu, yang menarik perhatian ramai ulama yang mengikutinya. Antaranya ialah ahli matematik Perancis yang kesembilan belas, Edouard Lucas, yang ketika mempelajari penggantian membaptisnya dengan nama Sage Abad Pertengahan yang membuatnya dikenali di Barat.

Masalah arnab fibonacci

Masalahnya mengatakan: terdapat beberapa arnab yang hidup selama -lamanya, yang pada dua bulan subur. Sebaik sahaja kematangan dicapai, mereka mempunyai beberapa bayi yang berlainan seks setiap bulan, yang juga mengambil masa dua bulan untuk menghasilkan semula dan mempunyai beberapa arnab bulanan.

Boleh melayani anda: undang -undang de morgan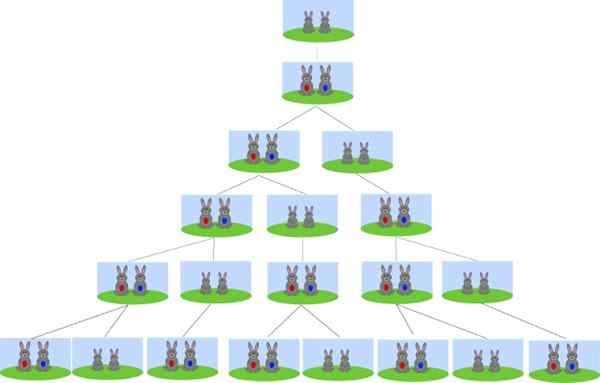Asal penggantian Fibonacci adalah dalam masalah pembiakan arnab. Sumber: Wikimedia Commons.

Bermula dengan beberapa arnab yang baru lahir, berapa pasang arnab dalam sebulan? Berapa pasang arnab selepas 2, 3 dan 4 bulan? Dan berapa banyak yang akan berlaku selepas 6 bulan?

Jawapannya ada dalam nombor Fibonacci. Selepas 1 bulan terdapat 1 sepasang arnab, pasangan asal, kerana mereka hanya menghasilkan semula selepas 2 bulan.

Selepas 2 bulan terdapat 2 pasangan arnab: pasangan asal dan sampah pertama mereka.

Pada 3 bulan, kami akan mempunyai 3 pasangan, termasuk pasangan asal, sampah pertama dan yang baru.

Setelah mencapai bulan ke -4, kami akan mempunyai pasangan asal, sampah pertama yang pada gilirannya mempunyai anak -anak pertama mereka, sampah bulan ketiga dan sampah baru. Sejumlah 5 pasang arnab.

Tetapi ini adalah bilangan urutan Fibonacci, oleh itu selepas 6 bulan akan ada 13 pasangan arnab, kerana setiap bulan pasangan dua bulan sebelumnya ditambah.

Siri Siri Fibonacci

Berikut adalah beberapa sifat menarik penggantian Fibonacci.

Harta 1

Formula rekursif untuk mencari syarat penggantian adalah:

ke_N+1 = a_n + ke_N-1  Untuk n lebih besar daripada atau sama dengan 2.

Di mana n = 2, 3, 4, ... iaitu, untuk mencari istilah ketujuh a₇, Kita lakukan n = 6, jadi 6+1 = 7. Kita perlu mengetahui syarat untuk₅  sudah₆, senarai yang muncul dalam pengenalan kepada₅ = 5 dan a₆ = 8, oleh itu ke₇ = 5+8 = 13.

Harta 2

Jika kedua -dua istilah yang kita mahu cari tidak diketahui, maka kita boleh menggunakan formula berikut:

Ia boleh melayani anda: tesseldos: ciri, jenis (biasa, tidak teratur), contoh

Harta 3

Nombor a_n sudah_N+1 adalah  Coprimos, iaitu, mereka adalah sepupu antara satu sama lain, yang bermaksud bahawa mereka tidak mempunyai persamaan yang sama.

Harta 4

Harta yang sangat menarik ialah kota antara terma ke_2n sudah_n, yang bernilai 1, ketika n = 1. Iaitu:

ke₂ / ke₁ = 1

Kami dapat dengan mudah menyemaknya dengan senarai nombor Fibonacci.

Sebaliknya, jika n ≠ 1, maka kuota adalah:

ke_2n / ke_n = a_n  + 2_N-1

Contohnya jika n = 3, maka a _2n = a₆ = 8 dan₃ = 2. Baiklah:

8/2 = 2 + 2. ke₂ = 2 + 2. 1

Sesungguhnya: 8/2 = 4 dan 2 + (2.1) = 4. Dapat disahkan bahawa sebarang nilai n dipenuhi.

Harta 5

Nisbah r_n = a_N+1 / ke_{n ,} Apabila n menjadi hebat, berkumpul ke Alasan emas Sama ada Perkadaran aurea, Nombor tidak rasional yang sering timbul dalam alam semula jadi, yang diberikan oleh:

Hubungan semula jadi penggantian Fibonacci

Penggantian Fibonacci dalam Tumbuhan

Manifestasi penggantian Fibonacci berlimpah di kerajaan tumbuhan

Cabang -cabang pokok -pokok tertentu keluar setiap tahun mengikut penggantian Fibonacci. Tahun pertama batang tumbuh tanpa membuang mana -mana cawangan, selepas satu tahun ia menghasilkan satu dan selama setiap tahun. Sebaliknya, setiap cawangan boleh membuang satu lagi yang baru selepas satu tahun, sama seperti arnab menghasilkan semula.

Pusat bunga bunga matahari mengandungi benih yang disusun dalam rasuk lingkaran logaritma, dalam kedua -dua erti kata, yang jumlahnya sesuai dengan dua nombor fibonacci berturut -turut.

Nombor Fibonacci terdapat dalam bilangan bunga matahari dan kelopak bunga margarit, serta dalam banyak corak di mana tumbuhan mempunyai daun mereka.

Boleh melayani anda: pemboleh ubah ordinal

Pakar mengatakan bahawa dengan cara ini tumbuh -tumbuhan mengoptimumkan ruang untuk daun dan bunga untuk mempunyai pertumbuhan yang optimum.

Dengan titik pusat sebagai tempat permulaan, struktur ini tumbuh dan menerima cahaya matahari, oleh itu daun dan kelopak baru mesti menutupi sebanyak mungkin yang keluar pertama. Dan cara terbaik untuk mencapai matlamat ini adalah menggunakan corak pertumbuhan dari segi urutan Fibonacci.

Penggantian Fibonacci pada haiwan

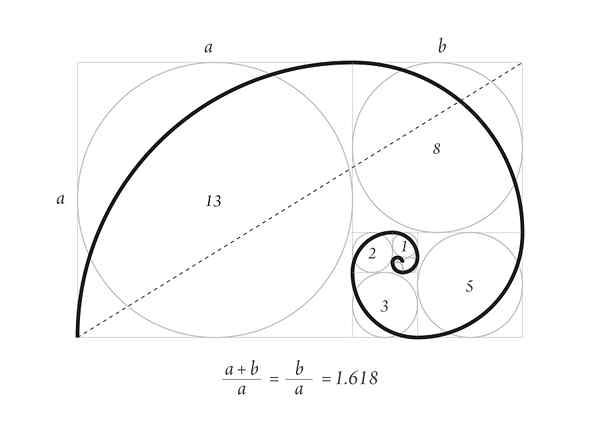Spiral Durero dengan jumlah pertama penggantian Fibonacci

Lingkaran tahan lama imej unggul adalah sebahagian daripada corak pertumbuhan cengkerang pada haiwan laut dan tanduk beberapa ruminan.

Mulakan dengan dua dataran 1, satu di atas yang lain, kemudian satu persegi sisi 2 di sebelahnya, yang membentuk segi empat tepat sisi 3, yang sisinya mempunyai bahagian emas.

Di bawah adalah persegi sisi 3 dan ke kiri persegi sisi 5. Di atas terdapat persegi sisi 8 dan ke kanan persegi sisi 13. Ini adalah nombor pertama penggantian.

Akhirnya lingkaran ditarik dengan menyentuh titik -titik sudut dataran, seperti yang dilihat dalam angka itu.

Aplikasi

Penggantian Fibonacci digunakan dalam pelbagai bidang:

-Dalam seni perkadaran emas yang berkaitan dengan penggantian Fibonacci muncul dalam orang dan perkara yang diwakili oleh artis hebat seperti Leonardo da Vinci, Miguel ángel dan Alberto Durero.

-Perkadaran rakan kongsi di Athens juga bertindak balas terhadap nombor emas.

-Dalam komposisi Mozart, Beethoven, Schubert dan Debussy.

-Untuk merancang objek yang perkadarannya kelihatan harmoni dengan mata manusia, seperti kad kredit, bekas, bendera.

-Di pasaran saham, ia digunakan untuk meramalkan harga berapa trendnya.

Rujukan

1. Penggantian Fibonacci. Pulih dari: blogeducastur.adalah.
2. Stewart, J. 2007. Precalculation. 5th. Edisi. Pembelajaran Cengage.
3. Vargas, m. Aplikasi penggantian Fibonacci. Pulih dari: matesup.Cl.
4. Wikipedia. Nombor Fibonacci. Diperoleh dari: dalam.Wikipedia.org.