Siri contoh dan latihan kuasa

A Siri kuasa Ia terdiri daripada jumlah istilah dalam bentuk kuasa pembolehubah x, atau lebih umum, dari X-C, di mana c Ia adalah nombor sebenar yang berterusan. Dalam penjumlahan jumlah siri kuasa ia dinyatakan seperti berikut:

Σa_n (X -c)ⁿ = a_{Sama ada} + ke₁ (x - c) + a₂ (X - c)² + ke₃ (X - c)³ +... + a_n (X - c)ⁿ

Di mana koefisien ke_{Sama ada}, ke₁, ke₂... Mereka adalah nombor sebenar dan siri bermula pada n = 0.

Rajah 1. Definisi siri kuasa. Sumber: f. Zapata.

Siri ini memberi tumpuan kepada nilai c itu tetap, tetapi anda boleh memilihnya c Sama dengan 0, dalam hal ini kuasa dipermudahkan:

Σa_n xⁿ = a_{Sama ada} + ke₁ x + a₂ x² + ke₃ x³ +... + a_n xⁿ

Siri ini bermula dengan ke_{Sama ada}(X-c)⁰ dan ke_{Sama ada}x⁰ masing -masing. Tetapi kita tahu bahawa:

(X-c)⁰= x⁰ = 1

Oleh itu ke_{Sama ada}(X-c)⁰ = ke_{Sama ada}x⁰ = ke_{Sama ada} (Istilah bebas)

Perkara yang baik tentang kuasa kuasa adalah bahawa dengan mereka anda dapat menyatakan fungsi dan ini mempunyai banyak kelebihan, terutama jika anda ingin bekerja dengan fungsi rumit.

Apabila ini berlaku, bukannya menggunakan fungsi secara langsung, pembangunan kuasa digunakan, yang boleh menjadi lebih mudah untuk memperoleh, mengintegrasikan, atau bekerja secara berangka.

Sudah tentu semuanya dikondisikan untuk penumpuan siri ini. Satu siri menumpu apabila dengan menambahkan sejumlah terma, nilai tetap diperolehi. Dan jika kita menambah lebih banyak istilah, kita terus memperoleh nilai itu.

[TOC]

Fungsi sebagai kuasa kuasa

Sebagai contoh fungsi yang dinyatakan sebagai satu siri kuasa, mari kita ambil f (x) = e^x.

Fungsi ini boleh dinyatakan dari segi satu siri kuasa seperti berikut:

dan^x  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Di mana! = n. (N-1). (N-2). (N-3) ... dan ia diambil 0! = 1.

Kami akan menyemak dengan bantuan kalkulator, yang siri ini bertepatan dengan fungsi yang diberikan secara eksplisit. Contohnya, mari kita mulakan x = 0.

Boleh melayani anda: kebarangkalian teoritis: bagaimana untuk mengeluarkannya, contoh, latihan

Kita tahu bahawa e⁰ = 1. Mari lihat apa siri ini:

dan⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +... = 1

Dan sekarang mari kita cuba x = 1. Kalkulator membuangnya dan¹ = 2.71828, Dan kemudian mari kita bandingkan dengan siri ini:

dan¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) + ... = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +... ≈ 2.7167

Dengan hanya 5 istilah kita sudah mempunyai kebetulan yang tepat E ≈ 2.71. Siri kami hilang sedikit lagi, tetapi lebih banyak istilah ditambah, dengan kepastian siri ini menumpu kepada nilai tepat dan. Perwakilannya tepat ketika N → ∞.

Sekiranya analisis sebelumnya diulangi untuk n = 2 Hasil yang sangat serupa diperolehi.

Dengan cara ini kita yakin bahawa fungsi eksponen f (x) = e^x Ia boleh diwakili oleh siri kuasa ini:

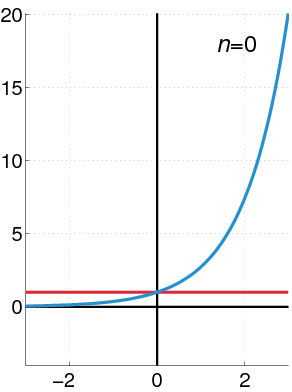Rajah 2. Dalam animasi ini, ia dilihat sebagai kuasa lebih dekat dengan fungsi eksponen kerana lebih banyak istilah diambil. Sumber: Wikimedia Commons.

Kuasa geometri kuasa

Fungsinya f (x) = e^x Ia bukan satu -satunya fungsi yang mengakui perwakilan kuasa bersiri. Contohnya, fungsi  F(x) = 1/1 - x  Ia kelihatan seperti yang diketahui Siri geometri konvergen:

Σa.rⁿ = A / 1 - r

Hanya lakukan a = 1 dan r = x untuk mendapatkan siri yang sesuai untuk fungsi ini, yang berpusat pada c = 0:

Walau bagaimanapun, diketahui bahawa siri ini adalah konvergen untuk │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Apabila anda ingin menentukan fungsi ini dalam selang waktu yang lain, ia hanya memberi tumpuan kepada nilai yang mencukupi dan siap.

Cara Mencari Perkembangan Siri Kekuatan Fungsi

Mana -mana fungsi boleh dibangunkan dalam satu siri kuasa yang difokuskan pada c, selagi anda berasal dari semua pesanan di x = c. Prosedur menggunakan teorem berikut, yang dipanggil Teorem Taylor:

Biarkan f (x) menjadi fungsi dengan derivatif pesanan n, dilambangkan sebagai F^(N), yang mengakui perkembangan siri kuasa dalam selang waktu Yo. Perkembangannya dalam Siri Taylor adalah:

Ia boleh melayani anda: Apakah lokasi keseluruhan dan nombor perpuluhan?

Jadi itu:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +... r_n

Di mana r_n, yang merupakan siri ini, ia dipanggil sisa:

Apabila C = 0 siri dipanggil Siri MacLaurin.

Siri ini yang diberikan di sini adalah sama dengan siri yang diberikan pada mulanya, hanya sekarang ada cara untuk mencari koefisien setiap istilah, yang diberikan oleh:

Walau bagaimanapun, perlu dipastikan bahawa siri ini menyampaikan fungsi yang anda mahu mewakili. Ia berlaku bahawa tidak setiap siri Taylor semestinya menumpu ke f (x) yang diingat ketika mengira koefisien ke_n.

Ini berlaku kerana mungkin yang berasal dari fungsi, dinilai di x = c bertepatan dengan nilai yang sama dari yang diperoleh dari yang lain, juga dalam x = c. Dalam kes ini, koefisien akan sama, tetapi pembangunan akan samar -samar dengan tidak mempunyai kepastian fungsi yang sepadan.

Nasib baik ada cara untuk mengetahui:

Kriteria Konvergensi

Untuk mengelakkan kekaburan, jika r_n → 0 Apabila n → ∞ Untuk semua x dalam selang I, siri ini menumpu ke f (x).

Senaman

- Latihan diselesaikan 1

Cari kuasa geometri untuk berfungsi f (x) = 1/2 - x Fokus pada C = 0.

Penyelesaian

Fungsi yang diberikan mesti dinyatakan dengan cara yang sepadan dengan sebanyak mungkin dengan 1 / 1- x, yang siri ini dikenali. Oleh itu, kami menulis semula pengangka dan penyebut, tanpa mengubah ungkapan asal:

1/2 - x = (1/2) / [1 - (x / 2)]

Oleh kerana ½ adalah malar, ia keluar dari jumlah, dan ini ditulis dari segi pembolehubah baru x/2:

Boleh melayani anda: Binomial konjugasi: Bagaimana ia diselesaikan, contoh, latihan

Perhatikan bahawa x = 2 tidak tergolong dalam domain fungsi, dan mengikut kriteria konvergensi yang diberikan dalam bahagian Siri Geometrik Kuasa, Pembangunan sah untuk │x/2│< 1 o equivalentemente -2 < x < 2.

- Latihan diselesaikan 2

Cari 5 syarat pertama perkembangan siri MacLaurin fungsi f (x) = sen x.

Penyelesaian

Langkah 1

Pertama adalah derivatif:

-Berasal dari perintah 0: ia adalah fungsi yang sama f (x) = sen x

-Derivatif Pertama: (sin x) '= cos x

-Derivatif Kedua: (sin x) "= (cos x) '= - sin x

-Derivatif Ketiga: (sin x) "= (-sen x) '= - cos x

-Derivatif keempat: (sin x) "= (- cos x) '= sin x

Langkah 2

Kemudian setiap derivatif dinilai pada x = c, seperti perkembangan maclaurin, c = 0:

dosa 0 = 0; cos 0 = 1; - sen 0 = 0; -COS 0 = -1; dosa 0 = 0

Langkah 3

Pekali dibina untuk_n;

ke_{Sama ada} = 0/0! = 0; ke₁ = 1/1! = 1; ke₂ = 0/2! = 0; ke₃ = -1 / 3!; ke₄ = 0/4! = 0

Langkah 4

Akhirnya siri ini dipasang mengikut:

dosa x ≈ 0.x⁰ + 1. x¹ + 0 .x² - (1/3!) x³ + 0.x⁴... = x - (1/3!)) x³  +…

Adakah pembaca memerlukan lebih banyak istilah? Berapa banyak lagi, siri ini lebih dekat dengan fungsi.

Perhatikan bahawa terdapat corak dalam koefisien, istilah bukan null berikut adalah untuk₅ Dan semua indeks ganjil juga berbeza dari 0, menggantikan tanda -tanda, supaya:

Sen x ≈ x - (1/3!)) x³  + (1/5!)) x⁵ - (1/7!)) x⁷  +… .

Ia ditinggalkan sebagai latihan untuk mengesahkan, anda boleh menggunakan Nisbah Kota Untuk penumpuan siri.

Rujukan

1. Yayasan CK-12. Siri Kuasa: Perwakilan Fungsi dan Operasi. Pulih dari: ck12.org.
2. Engler, a. 2019. Kalkulus integral. Universiti Kebangsaan Pantai.
3. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
4. Teks matematik percuma. Siri kuasa. Pulih dari: matematik.Liibretexts.org.
5. Wikipedia. Siri kuasa. Pulih dari: Adakah.Wikipedia.org.