Aplikasi, contoh dan latihan siri Fourier diselesaikan

The Siri Fourier Mereka terdiri daripada jumlah istilah tak terhingga, yang terdiri daripada fungsi harmonik, sinus dan kosinus, yang argumennya adalah asas keseluruhan frekuensi asas.

Fungsi sinus dan kosinus didarabkan dengan pekali nilai, sehingga jumlahnya sama dengan fungsi dengan tempoh t sama dengan dua kali pi (2π) dibahagikan dengan kekerapan sudut asas Ω Ω.

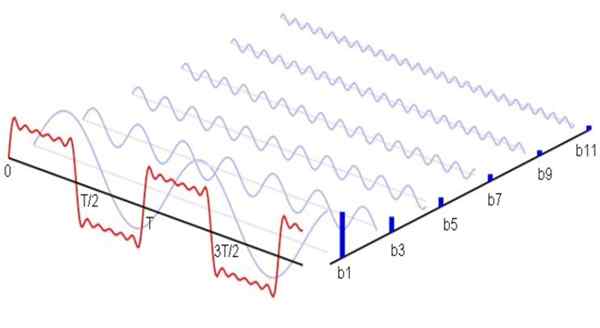
Rajah 1. Berikut adalah (berwarna biru) harmonik bukan null pertama siri Fourier yang sepadan dengan isyarat gelombang persegi. Jumlah harmonik ini menimbulkan isyarat merah. Sumber: Wikimedia Commons.

Secara matematik ia akan dinyatakan seperti berikut: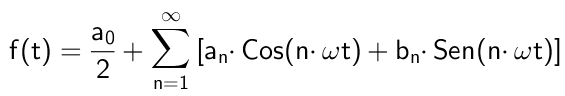

Di mana Ω Ini adalah kekerapan asas, yang berkaitan dengan tempoh tersebut T fungsi f (t) Melalui hubungan: 

Ω = 2π / t

Kerana menjadi tempoh berkala T, fungsinya f (t) memenuhi syarat ini:

f (t) = f (t + k t)

Di mana k Ia adalah integer dan pekali untuk₀ , ke_n dan b_n Mereka dipanggil Koefisien Fourier.

[TOC]

Kepentingan dan penggunaan siri Fourier

Nama siri Fourier adalah disebabkan oleh fakta bahawa penemunya adalah matematik Perancis.

Penemuan ini adalah asas bagi matematik, kerana jika persamaan pembezaan mempunyai penyelesaian harmonik tertentu, maka adalah mungkin untuk mencapai penyelesaian umum dengan cara bertindih atau jumlah yang sama.

Koefisien Fourier dari fungsi berkala, juga dipanggil tanda, Mereka adalah spektrum yang sama.

Oleh itu, spektrum adalah set frekuensi yang membentuk isyarat yang dicirikan oleh amplitud setiap kekerapan, yang sepadan dengan nilai pekali Fourier.

Sistem pemampatan isyarat atau bentuk gelombang audio dan video, di belakang bilangan bit yang lebih kecil daripada isyarat digital yang asal.

Siri Fourier dari isyarat adalah seperti cap jari, dalam erti kata bahawa, mengenali pekali yang membuatnya, anda selalu dapat mengetahui tanda yang mereka milik.

Walaupun penggunaan siri Fourier, atau bentuk yang paling umum, Transformasi Fourier, Sebagai kaedah pemampatan isyarat ia telah diketahui sejak sekian lama, penggunaannya dalam amalan perlu menunggu pemproses berangka dengan cepat, yang membolehkan isyarat dimampatkan dan dikompresi dalam "masa nyata".

Boleh melayani anda: Pembolehubah statistik

Contoh Siri Fourier 

Seterusnya, contoh fungsi f (t) dan siri Fouriernya.

Fungsinya ialah:

 f (t) = 0 ya 0 ≤ t  < π y 1 si π ≤  t   < 2π

Dan mempunyai siri Fourier yang sepadan dengan:

F (t) = ½ - 2/π ⋅se (t) - 2/(3π) ⋅Se (3t) - 2/(5π) ⋅sen (5t) - 2/(7π) ⋅sen (7t) - ..

Angka berikut menunjukkan fungsi dan jumlah separa siri Fourier:

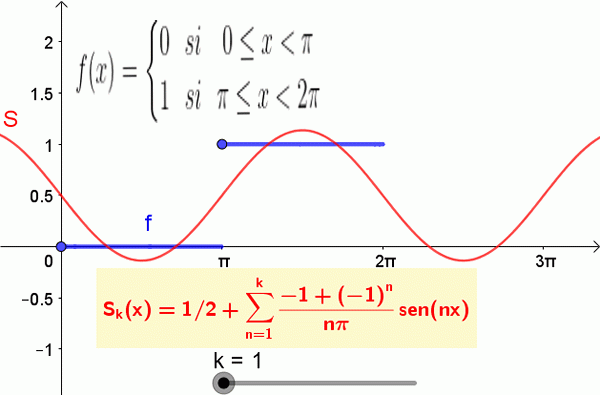Rajah 2. 19 syarat pertama jumlah Fourier yang sepadan dengan fungsi langkah ditunjukkan. Sumber: f. Zapata.

Penentuan koefisien

Berikut adalah cara menentukan pekali Fourier:

Katakan fungsi adalah f (x) yang ditakrifkan dalam selang yang pergi dari t_Yo ke t_Yo + T, di mana modal akan menjadi tempoh fungsi. Kemudian siri Fouriernya ialah:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) + ... + a_n Cos (n Ω t) +..

… .+ b₁ sin (Ω t) +b₂ dosa (2 Ω t) +... +b_n Dosa (n Ω t) +..

Pengiraan istilah bebas

Untuk mencari istilah bebas, kami mengintegrasikan kedua -dua ahli kesamaan dalam selang definisi fungsi:

[t_Yo , t_Yo+ T]

Oleh itu:

Sama_n ∫COS (n Ω t) dt +..

… .+ B₁ ∫sen (ω t) dt +b₂ ∫sen (2 Ω t) dt +... +b_n ∫sen (n Ω t) dt +..

Di sini simbol ∫ bermaksud integral yang ditakrifkan dari t_Yo ke t_Yo + T.

Integral istilah pertama adalah t, yang apabila dinilai dalam hasil had atasnya:

t_Yo + T

Apabila menolak had bawah t_Yo, Dalam t.

Semua istilah lain adalah 0, kerana ini adalah fungsi kosinus atau sinus yang dinilai dalam tempoh penuh, seperti yang kita tunjukkan di bawah:

∫COS (nΩ t) dt = (1/ nΩ) ∫COS (nΩ t) d (nΩ t)

Ingat bahawa simbol ∫ bermaksud integrasi antara t_Yo ke t_Yo + T. 

Untuk membuat integrasi istilah yang mempunyai kosinus atau payudara, kami akan membuat perubahan berikut pembolehubah:

x = ω (t - t_Yo)

Jadi pembezaan x, dx adalah sama dengan perbezaan d (ωt).

Oleh itu, integral yang akan dijalankan adalah:

Sebagai n adalah integer, maka integral yang ditakrifkan akan selalu memberi sifar. Perkara yang sama berlaku untuk fungsi sinus.

Oleh itu, integral yang ditetapkan dinilai dalam tempoh lengkap semua terma yang mengandungi. 

Boleh melayani anda: bahagian di mana sisa adalah 300

Oleh itu, disimpulkan bahawa istilah a₀ dikira seperti berikut:

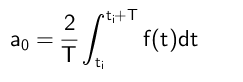
Pengiraan koefisien ke

Untuk mengira koefisien yang membiak fungsi kosinus, kedua -dua ahli kesamaan mesti didarab:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) + ... + a_n Cos (n Ω t) +..

… .+ b₁ sin (Ω t) +b₂ dosa (2 Ω t) +... +b_n Dosa (n Ω t) +..

Oleh fungsi kosinus yang dinilai dalam harmonik yang sepadan dan kemudian integral ditakrifkan dalam tempoh penuh kepada kedua -dua ahli digunakan. 

Contohnya, untuk mengira_m Kedua -dua ahli itu didarabkan oleh COS (MΩt):

F (t) cos (m Ω t) = a₀/2 cos (m ω t) + a₁ cos (Ω t) cos (m ω t) + a₂ cos (2 Ω t) cos (m ω t) + ... + ke_n Cos (n Ω t) cos (m Ω t) +..

… .+ b₁ sin (Ω t) cos (m Ω t) +b₂ sin (2 Ω t) cos (m Ω t) +... +b_n Dosa (n Ω t) cos (m Ω t) +..

Kemudian mengintegrasikan ke dalam tempoh yang lengkap, iaitu, dalam selang masa yang berlaku dari t_Yo ke t_Yo + T.

Integral istilah yang mengandungi A₀ dibatalkan, kerana M adalah integer dan fungsi kosinus diintegrasikan ke dalam tempoh penuh. 

Integral yang mengandungi produk COS (n Ω t) cos (m ω t) juga dibatalkan apabila n ≠ m. Hanya dalam kes bahawa n = m mempunyai integral:

Semua istilah yang mempunyai sinus didarabkan kosinus, iaitu, yang didarabkan oleh pekali B, seperti yang mengandungi integral jenis SEN (n Ω t) cos (m Ω t) dibatalkan apabila integral yang ditetapkan dilakukan secara lengkap tempoh. 

Dari sini disimpulkan bahawa:

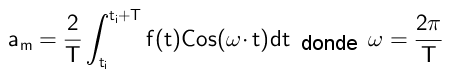
Pengiraan pekali b

Untuk mencari pekali B prosedur yang sama digunakan, tetapi kali ini kedua -dua ahli fungsi yang dipadankan dengan siri Fourier didarabkan oleh fungsi SEN (M Ω T).

Atas sebab yang sama telah dijelaskan untuk kes di mana satu -satunya istilah yang tidak dibatalkan selepas mengintegrasikan ke dalam tempoh yang lengkap adalah satu di mana:

n = m

Dan di mana integral [sen (m Ω t)] muncul]², yang disatukan pada tempoh yang lengkap menghasilkan π.

Boleh melayani anda: Fungsi homografi: Cara graf, latihan yang diselesaikan

Dengan cara ini, pekali B dikira mengikut formula berikut:

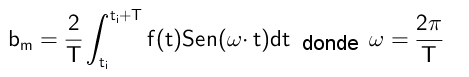
Latihan

- Latihan 1

Buat pengiraan eksplisit pekali fungsi

 f (t) = 0 ya 0 ≤ t  < π y 1 si π ≤  t   < 2π

Penyelesaian

Mula -mula kita mengenal pasti tempoh t fungsi ini sebagai 2π, jadi kekerapan asas Ω = 2π/ t dalam contoh ini adalah sama dengan unit, iaitu:

Ω = 1

Fungsi ini ditakrifkan dalam selang [0, 2π], jadi semua integrasi akan dijalankan dalam selang tersebut. 

Kemudian istilah bebas dikira seperti berikut:

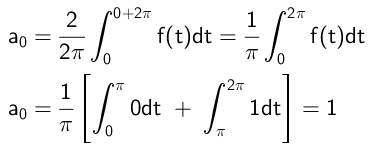
Koefisien yang melipatgandakan fungsi kosinus dikira dengan cara ini:

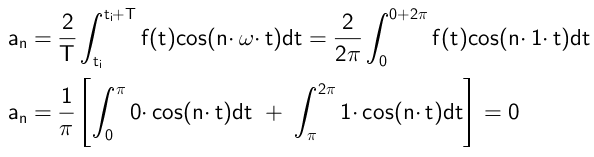
Seperti yang dapat dilihat, semua pekali untuk batal, yang akan berlaku dengan syarat fungsi f (t) adalah ganjil.

Begitu juga, pekali B akan dikira seperti berikut:

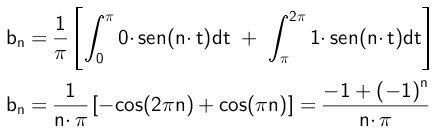
- Latihan 2

Cari pekali fungsi yang sepadan dengan Rajah 1, iaitu:

f (t) = -1 ya 0≤ t

Penyelesaian 

Oleh kerana fungsi mengambil nilai antara -1 dan +1, kita boleh intuit bahawa istilah bebas adalah tidak sah, namun kita akan mengira dengan jelas:

Kerana hakikat bahawa fungsi itu mempunyai simetri ganjil, semua pekali untuk melipatgandakan istilah harmonik dengan fungsi kosinus mesti dibatalkan. Kami mengesahkannya di bawah:

Akhirnya, kita akan menemui pekali B yang melipatgandakan istilah harmonik yang mengandungi fungsi sinus:

Di mana semua istilah b dengan subskrip diperhatikan adalah 0. Terma ganjil pertama adalah:

b₁= -4/(π); b₃= -4/(3π); b₅= -4/(5π); b₇= -4/(7π) dan B₉= -4/(9π)

https: // youuat.Be/737yagwszya

Rujukan

1. Amerror, i. 2013. Menguasai transformasi Fourier diskret dalam satu, dua atau beberapa dimensi: perangkap dan artifak. Media Sains & Perniagaan Springer.
2. Briggs, w. Sembilan-belas sembilan puluh lima. DFT: Manual Pemilik untuk Transformasi Fourier Diskret. Siam.
3. Chu, e. 2008. Transformasi Fourier yang diskret dan berterusan: Analisis, Aplikasi dan Algoritma Cepat. CRC Press.
4. Guoan BI, Yonghong Zeng. 2012. Mengubah dan Algoritma Cepat untuk Analisis dan Perwakilan Isyarat. Media Sains & Perniagaan Springer.
5. Sundararajan, d. 2003. Pemprosesan Isyarat Digital: Teori dan Amalan.Saintifik Dunia. 
6. Wikipedia. Siri Fourier. Pulih dari: Adakah.Wikipedia.com