Pengagihan Kekerapan Cara Membuat Jadual, Contoh, Latihan

A Pengagihan kekerapan Dalam statistik ia merujuk kepada trend yang mengikuti data yang dianjurkan dalam kumpulan, kategori atau kelas, apabila masing -masing diberikan nombor yang dipanggil frekuensi, yang menunjukkan berapa banyak data yang ada dalam setiap kumpulan. 

Sebagai peraturan, diperhatikan bahawa frekuensi ini diedarkan di sekitar kumpulan pusat: yang mempunyai bilangan data tertinggi.

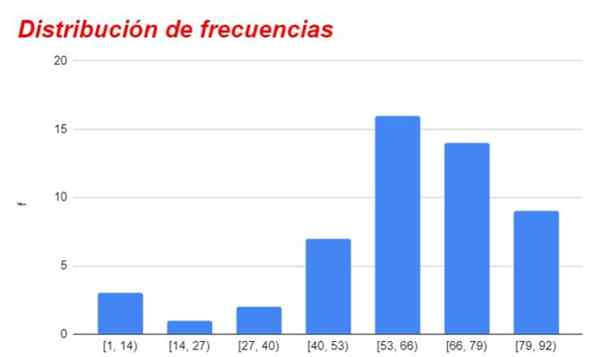
Rajah 1. Carta pengagihan kekerapan yang diperoleh dari jadual yang sepadan. Sumber: f. Zapata.

Kumpulan yang berada di atas atau di bawah kata kategori pusat secara beransur -ansur mengurangkan kekerapannya, sangat kecil atau tidak penting untuk kategori paling jauh dari kategori dengan kekerapan yang lebih tinggi.

Cara mengetahui pengagihan frekuensi set data terdiri daripada membuat kategori dan kemudian membuat jadual kekerapan. Perwakilan visual jadual kekerapan dipanggil histogram.

[TOC]

Jenis kekerapan

Terdapat beberapa jenis frekuensi:

1.- Frekuensi mutlak: Ia adalah yang paling asas, dan daripadanya yang lain dibina. Ia hanya terdiri daripada jumlah data yang sepadan dengan kategori.

2.- Frekuensi relatif: Adalah kekerapan mutlak setiap kategori yang dibahagikan dengan jumlah data.

3.- Frekuensi peratusan: Ia adalah kekerapan relatif yang sama tetapi didarabkan dengan seratus, menunjukkan peratusan nilai penampilan dalam setiap kategori.

4.- Kekerapan terkumpul: Ia adalah jumlah frekuensi mutlak kategori yang lebih rendah atau sama dengan kategori yang sedang dipertimbangkan. 

5.- Peratusan kekerapan terkumpul: Ia adalah jumlah frekuensi peratusan kategori yang lebih rendah atau sama dengan kategori yang diperhatikan.

Langkah untuk membuat jadual pengedaran frekuensi

Terdapat beberapa langkah yang harus diikuti untuk membina jadual pengedaran frekuensi.

Di tempat pertama, data mesti pokok, dll.

Boleh melayani anda: Apakah pembahagi 30? (Penjelasan)

Langkah 1

Kenal pasti nilai minimum Xmin dan nilai maksimum Xmax Dalam set data x.

Langkah 2

Kirakan julat r, yang ditakrifkan sebagai perbezaan antara nilai maksimum kurang nilai minimum: r = xmax - xmin.

Langkah 3

Tentukan nombor k selang waktu atau kelas, yang mungkin telah ditetapkan. Jumlah k akan menentukan bilangan baris yang akan dimiliki oleh jadual kekerapan.

Langkah 4

Sekiranya bilangan selang waktu k Ia tidak diberikan sebelumnya, maka ia mesti ditubuhkan mengikut garis panduan berikut: bilangan kategori yang disyorkan adalah 5, tetapi mungkin lebih tinggi di mana ia lebih baik memilih nombor ganjil.

Langkah 5

Terdapat formula yang dipanggil Peraturan Sturges yang memberi kita bilangan selang waktu k disyorkan untuk satu set yang terdiri daripada N data:

K = [1 + 3,322 ⋅log n]

Hasilnya dalam pendakap pasti akan menjadi nombor sebenar, pendakap menunjukkan bahawa ia mesti dibulatkan kepada integer ganjil yang paling dekat untuk mendapatkan nilai integer k.

Langkah 6

Amplitud dikira Ke dari setiap selang (kelas atau kategori) yang mengambil kuota antara julat R dan bilangan selang waktu k: A = r/k. Sekiranya data asal adalah nombor keseluruhan, maka integer terdekat dibulatkan, jika tidak nilai sebenarnya ditinggalkan.

Langkah 7

Tentukan had bawah dan atas setiap selang atau kelas. Selang pertama, atau kelas terendah, mempunyai had yang lebih rendah yang terkecil dari data asal, iaitu, li = xmin dan sebagai had atas nilai minimum ditambah amplitud selang, ini adalah ls = xmin + a. 

Langkah 8

Selang berturut -turut adalah: 

[Xmin, xmin + a), [ Xmin + a, xmin + 2 ⋅ a), ... [ Xmin + (k-1) a, xmin + k angani).

Boleh melayani anda: Operasi gabungan

Langkah 9

Jenama kelas XC ditentukan untuk setiap selang, menggunakan formula berikut: Xc = (ls - li) / 2 + li.

Langkah 10

Tajuk jadual kekerapan diletakkan, yang terdiri daripada baris dengan label berikut: kelas, jenama kelas XC, kekerapan F, frekuensi relatif F (atau peratusan frekuensi f%) dan kekerapan terkumpul F (atau kekerapan peratusan terkumpul f%).

Apa yang akan kita ada seterusnya adalah perkara berikut:

Lajur pertama jadual kekerapan: mengandungi selang atau kelas di mana data telah dibahagikan.

Lajur kedua: mengandungi jenama kelas (atau titik pertengahan) dari setiap subinterval.

Lajur ketiga: Mengandungi kekerapan mutlak f setiap kelas atau kategori.

Lajur Keempat dan Kelima: nilai yang sepadan dengan kekerapan relatif (atau peratusan) dan kekerapan terkumpul F (atau peratusan terkumpul) diletakkan.

Contoh pembinaan jadual

Data berikut sesuai dengan jawapan yang tepat dari 100 soalan yang digunakan untuk sekumpulan 52 pelajar:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55. 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48. 64, 15, 50.

Kami akan mengikuti langkah -langkah untuk membina jadual kekerapan:

1.- Nilai minimum dan maksimum xmin = 1, xmax = 89.

2.- Julatnya ialah: r = 89 - 1 = 88

3.- Penentuan bilangan selang mengikut Peraturan Sturges: K = [1 + 3,322 ⋅log 52] = [6,70] = 7.

4.- Pengiraan lebar selang: a = r / k = 88/7 = 12.57 ≈ 13.

5.- Selang adalah: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- Jenama kelas setiap selang ditentukan: 8, 21, 34, 47, 60, 73 dan 86.

7.- Jadual dibuat:

Boleh melayani anda: Sudut konjugasi dalaman dan luaran: Contoh, Latihan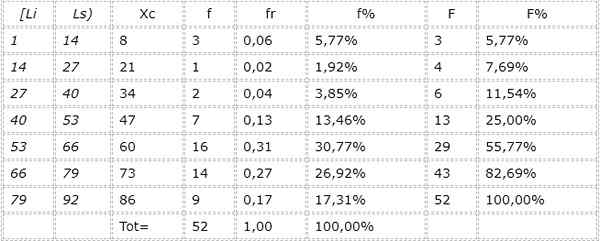

Grafik frekuensi untuk selang atau kategori yang berbeza ditunjukkan dalam Rajah 1.

Latihan diselesaikan

Seorang guru merekodkan peratusan objektif yang dicapai dalam subjek fizik untuk setiap pelajar. Walau bagaimanapun, kelayakan kepada setiap pelajar, walaupun ia bergantung kepada peratusan objektif yang dicapai, adalah ketat kepada kategori tertentu yang sebelum ini ditubuhkan dalam Peraturan Pengajian Universiti.

Mari kita lihat kes tertentu: Di bahagian fizik anda mempunyai peratusan objektif yang dicapai untuk setiap 52 pelajar: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61. 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61. 65, 70, 89, 64, 54, 85. 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

Dalam contoh ini, kategori atau kelas sesuai dengan kelayakan akhir yang diberikan mengikut peratusan X objektif yang dicapai:

1.- Sangat miskin: 1 ≤ x < 30

2.- Miskin: 30 ≤ x < 50

3.- Cukup: 50 ≤ x < 70

4.- Nah: 70 ≤ x < 85

5.- Cemerlang: 85 ≤ x ≤ 100

Untuk membuat jadual kekerapan, data diperintahkan dari yang paling sedikit ke yang paling besar dan memberitahu berapa banyak data yang sesuai dengan setiap kategori, yang akan menjadi kelayakan yang akan diperoleh oleh pelajar dalam subjek fizik:

1.- Sangat miskin: 4 pelajar.

2.- Miskin: 6 pelajar.

3.- Cukup: 20 pelajar.

4.- Baiklah: 17 pelajar.

5.- Cemerlang: 5 pelajar.

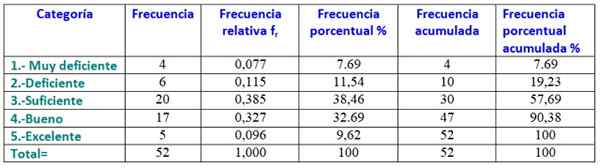
Berikut adalah histogram gred, yang dibina dari jadual sebelumnya:

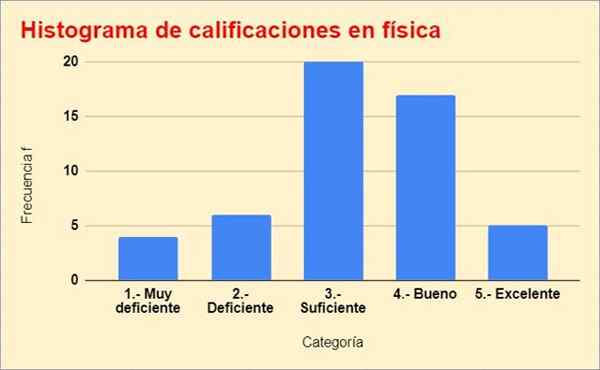Rajah 2. Graf pengedaran frekuensi latihan diselesaikan. Sumber: f. Zapata.

Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
3. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
4. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
5. Spiegel, m. 2009. Statistik. Siri Schaum. 4 ta. Edisi. McGraw Hill.
6. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.