Penggantian kompaun

Penggantian terdiri daripada dataran kuning dan biru. Sumber: f. Zapata

Apakah penggantian komposit?

A penggantian kompaun Ia terdiri daripada urutan elemen, yang dibuat dari dua (atau lebih) penggantian yang berbeza dan alternatif. Setiap penggantian ini mempunyai peraturan tertentu, yang digunakan untuk mencari elemen masing -masing.

Unsur -unsur tidak perlu berangka, dapat menjadi angka, simbol atau huruf, tetapi yang berdasarkan nombor dipanggil Penggantian aritmetik. Angka yang dimulakan artikel kami menunjukkan penggantian kompaun dari dataran kuning dan biru.

Dalam penggantian ini, ia bermula dari dataran besar yang terdiri daripada 8 dataran kuning dan dataran biru. Untuk mendapatkan istilah berikut, dataran kuning ditambah ke kiri atau kanan baris pertama dan ketiga dataran. Ruang yang mengakibatkan barisan tengah dipenuhi dengan dataran biru.

Setiap angka dalam urutan dipanggil istilah. Jika anda ingin mencari penggal kelima, anda perlu menambah dataran kuning di sebelah kanan pangkat pertama dan ketiga, dan dataran biru di barisan kedua:

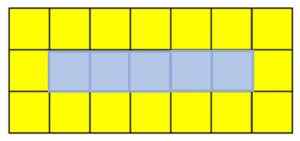Tempoh kelima berturut -turut dataran kuning dan biru. Sumber: f. Zapata

Penjelasan

Dalam penggantian kompaun, terma diperolehi dengan menggantikan syarat dua atau lebih penggantian mudah bebas. Untuk lebih memahami idea itu, ia harus mengkaji semula butiran penggantian yang mudah.

Sebagai contoh, penggantian mudah berikut terdiri daripada nombor semula jadi:

2, 4, 6, 8, 10, 12 ..

Titik yang menggalakkan menunjukkan bahawa penggantian mempunyai istilah yang tidak terhingga.

Setiap istilah dilambangkan oleh surat kecil dan nombor, sebagai subskrip. Nombor ini menunjukkan kedudukan atau indeks setiap istilah. Dalam penggantian sebelumnya, anda boleh menulis:

ke₁ = 2; ke₂ = 4; ke₃ = 6; ke₄ = 8 ..

Sangat mudah untuk mempunyai cara untuk mengira apa -apa istilah yang dikehendaki penggantian, iaitu peraturan tertentu. Dengan dia Istilah N-ésimo, Sama ada Istilah umum, dilambangkan sebagai a_n.

Boleh melayani anda: sifat kesamaan

Meneruskan dengan contoh penggantian nombor walaupun, anda boleh menetapkan cara untuk mengira istilah n-ésimo, dari istilah sebelumnya:

ke_n = a_N-1 + 2

Kemana_N-1 Ia adalah istilah yang mendahului_n.

Sudah tentu lebih baik mengetahui istilah umum tanpa bergantung pada syarat lain. Dalam penggantian ini, mudah untuk diperhatikan bahawa mana -mana istilah mengalikan dengan 2 kedudukan yang ditempati, memandangkan subskrip istilah. Dengan cara ini ditulis:

ke_n = 2n

Orang Yunani Kuno sudah mengetahui penggantian nombor walaupun dan ganjil. Sementara itu, penggantian nombor semulajadi ganjil, boleh ditulis sebagai:

1, 3, 5, 7, 9, 11 ..

Dan menggabungkan penggantian nombor -nombor walaupun dengan ganjil, penggantian kompaun berikut adalah:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Yang hasilnya adalah set nombor semula jadi.

Syarat Penggantian Kompaun

Mungkin menyeronokkan untuk mencari hubungan yang wujud dalam urutan nombor, yang mana ia mesti diperhatikan dengan teliti dan cuba mengenal pasti jika ia adalah penggantian komposit.

Bentuk umum penggantian yang terdiri daripada dua penggantian akan menjadi:

ke₁, b₁, ke₂, b₂, ke₃, b₃, ke₄, b₄,…

Kemana₁, ke₂, ke₃, ke₄,... adalah syarat penggantian pertama dan b₁, b₂, b₃, b₄,... yang kedua. Mereka sentiasa diselingi, seperti halnya dalam contoh ini:

7, 8, 14, 16, dua puluh satu, 24, 28, 32, 35…

Apa yang akan menjadi istilah yang berikut?

Untuk mengetahui, ketahui penggantian dalam dua set nombor alternatif, seperti berikut:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

Pada yang pertama set ini, gandaan 7 muncul:

ke₁ = 7 × 1 = 7; ke₂ = 7 × 2 = 14; ke₃ = 7 × 3 = 21; ke₄ = 7 × 4 = 28; ke₅ = 7 × 5 = 35

Tempoh umum penggantian ini adalah:

ke_n = 7n

Dan pada yang kedua, ia adalah gandaan 8:

b₁ = 8 × 1 = 8; b₂ = 8 × 2 = 16; b₃ = 8 × 3 = 24; b₄ = 8 × 4 = 32

Jadi istilah umum adalah:

Ia dapat melayani anda: fungsi pembolehubah sebenar dan perwakilan grafiknya

b_n = 8n

Kembali ke penggantian kompaun yang asal, 35 milik urutan pertama, yang terma₁, ke₂, ke₃, ke₄ ... 35 adalah penggal kelima, jadi istilah yang berikut harus b₅, yang mudah diperoleh dari peraturan untuk mencari istilah umum:

b₅ = 8 × 5 = 40

Dan ia ditulis:

7, 8, 14, 16, dua puluh satu, 24, 28, 32, 35, 40 ..

Contoh penggantian komposit

Contoh 1

Anda boleh membuat penggantian komposit dengan angka geometri, seperti persegi dan bulatan, mengaturnya seperti yang ditunjukkan di bawah:

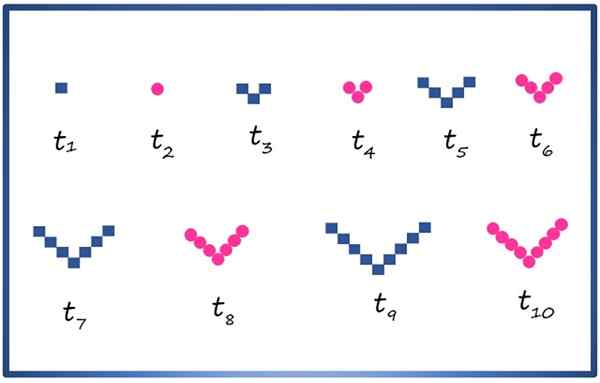10 syarat pertama penggantian komposit dengan elemen geometri persegi dan bulatan. Sumber: f. Zapata

Setiap istilah dilambangkan oleh t₁, t₂, t₃, t₄ ..., syarat indeks parque terdiri daripada bulatan dan indeks ganjil, dataran. Berhati -hati memerhatikan urutan yang mungkin diketahui, sebagai contoh, istilah t_sebelas, Itu tidak muncul dalam imej, terdiri daripada 11 dataran dengan peruntukan dalam v.

Contoh 2

Penggantian komposit berikut terdiri daripada simbol, dalam kes ini, huruf r dan s:

R SS RR SSS RRR SSS RRRR SSSS RRRR SSSSSS ..

Setiap istilah baru dibina dengan menambahkan surat kepada yang sebelumnya. Empat syarat pertama urutan yang ditunjukkan adalah:

t₁= R ; t₂= H.H ; t₃= Rr ; t₄= SSS …

Dan istilah seterusnya yang akan muncul selepas istilah yang ditunjukkan adalah:

t_sebelas= Rrrrrrr

Contoh 3

Contoh sebelumnya menunjukkan kejayaan menaik, di mana setiap nilai meningkat, dalam beberapa cara, berkenaan dengan sebelumnya. Tetapi ia tidak semestinya harus dengan cara ini, kerana penggantian dapat turun, iaitu, mereka mempunyai corak penurunan.

Dan penggantian menaik dapat digabungkan dengan penggantian menurun.

Penggantian berangka berikut disusun:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Ia boleh dipisahkan menjadi dua penggantian:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Apakah nilai -nilai yang mesti diletakkan di ruang kosong?

Berhati -hati memerhatikan penggantian pertama, setiap istilah diperoleh dengan menambahkan 3 ke istilah sebelumnya. Oleh itu, ia adalah penggantian menaik:

Boleh melayani anda: anjakan sudut

7 = 4 + 3

10 = 7 + 3

Oleh itu, di ruang kosong pertama yang perlu anda letakkan:

10 + 3 = 13

Selepas ini, istilah berikut adalah, sebenarnya:

16 = 13 + 3

Dan yang masuk kosong adalah:

16 + 3 = 19

Penggantian kedua turun dan sangat mudah untuk mencari istilah yang hilang, kerana diperhatikan bahawa setiap istilah diperoleh dengan menolak 1 dari istilah sebelumnya, oleh itu:

36, 35, 3. 4, 33, 32…

Akhirnya, anda boleh menulis:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,…

Latihan yang diselesaikan

Latihan 1

Dalam penggantian yang terdiri daripada Contoh 3 di bahagian sebelumnya:

a) Adakah 29 milik penggantian tersebut?

b) Tulis 10 lagi syarat penggantian ini

Jawapan kepada

Ya itu milik, kerana penggantian kedua turun dan syaratnya diperoleh dengan menolak 1 dari istilah sebelumnya. Dengan cara ini, akhirnya mencapai 29.

Jawab b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Perhatikan bahawa beberapa istilah diulang.

Latihan 2

Cari istilah yang hilang dalam penggantian kompaun berikut:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Jawapan

Istilah ganjil ditulis untuk mendapatkan penggantian pertama:

100, 115, 130, 145, 160, ..

Diperhatikan bahawa, untuk mencari setiap istilah, anda perlu menambah 15 pada masa sebelumnya, oleh itu, istilah yang berikut pada 160 adalah 175.

Penggantian kedua terdiri daripada:

500, 480, 460, 440, 420, ..

Setiap istilah berbeza dari yang sebelumnya hingga 20, penggantian yang turun, oleh itu, istilah yang diikuti pada 420 adalah 400.

Dengan maklumat ini, dua lagi istilah ditambah kepada penggantian kompaun asal, seperti ini:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Rujukan

1. Larson, r. (2012). Precalculation. Ke -8. Edisi. Pembelajaran Cengage.
2. Stewart, J. (2007). Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
3. Penggantian komposit. Pulih dari: media.EducacionCampe.Gob.mx.
4. Penggantian berangka. Diperolehi dari: Matemathweb.com.
5. Kejayaan. Perkembangan aritmetik dan geometri. Diperolehi daripada: MacmillanEducation.adalah.