Jumlah polinomial, seperti yang dilakukan, contoh, latihan

The Jumlah polinomial Ia adalah operasi yang terdiri daripada menambah dua atau lebih polinomial, mengakibatkan polinomial lain. Untuk melaksanakannya adalah perlu untuk menambah syarat urutan yang sama dari setiap polinomial dan menunjukkan jumlah yang dihasilkan.

Mula -mula kita mengkaji secara ringkas makna "syarat perintah yang sama". Polinomial seseorang terdiri daripada jumlah dan/atau penolakan terma.

Rajah 1. Untuk menambah dua polinomial, perlu memerintahkannya dan kemudian mengurangkan istilah yang serupa. Sumber: Pixabay + Wikimedia Commons.

Istilah boleh menjadi produk nombor sebenar dan satu atau lebih pembolehubah, diwakili dengan huruf, contohnya: 3x² dan -√5.ke²BC³ Mereka adalah istilah.

Nah, syarat perintah yang sama adalah mereka yang mempunyai eksponen atau kuasa yang sama, walaupun mereka mungkin mempunyai pekali yang berbeza.

-Syarat Perintah Sama adalah: 5x³, √2 x³ dan -1/2x³

-Syarat pesanan yang berbeza: -2x^-2, 2xy^-1 dan √6x²dan

Penting untuk diingat bahawa hanya syarat -syarat perintah yang sama dapat ditambah atau dikurangkan, operasi yang dikenali sebagai pengurangan. Jika tidak, jumlahnya hanya ditunjukkan.

Sebaik sahaja konsep syarat -syarat perintah yang sama dijelaskan, polinomial ditambah berikutan langkah -langkah ini:

-Pesanan Mula -mula polinomial untuk menambah, semuanya dengan cara yang sama, sama ada meningkat atau berkurang, iaitu, dengan kuasa -kuasa dari yang paling sedikit ke yang paling besar atau sebaliknya.

-Untuk melengkapkan, Sekiranya ada kuasa dalam urutan yang hilang.

-Mengurangkan Istilah yang sama.

-Menunjukkan Jumlah yang terhasil.

[TOC]

Contoh jumlah polinomial

Kami akan mulakan dengan menambahkan dua polinomial dengan pembolehubah tunggal yang dipanggil x, Contohnya polinomial p (x) dan q (x) yang diberikan oleh:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Berikutan langkah -langkah yang diterangkan, ia bermula dengan memerintahkannya dengan menurun, yang merupakan cara yang paling biasa:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Ia boleh melayani anda: sudut tertulis bulatan: definisi, teorem, contoh

Q (x) = x⁵+ x² - 25x

Polinomial q (x) tidak lengkap, dilihat bahawa kuasa dengan eksponen 4, 3 dan 0. Yang terakhir hanyalah istilah bebas, yang tidak mempunyai surat.

Q (x) = x⁵+ 0x⁴ + 0x³ + x² - 25x + 0

Setelah langkah ini selesai, mereka sudah bersedia untuk menambah. Anda boleh menambah istilah yang sama dan kemudian menunjukkan jumlah, atau letakkan polinomial yang diperintahkan oleh satu sama lain dan mengurangkan lajur, dengan cara ini:

- x⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ x⁵ + 0x⁴ + 0x³  +  x²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = p (x) + q (x)

Penting untuk diperhatikan bahawa apabila ditambah, ia dilakukan secara algebra menghormati peraturan tanda, dengan cara ini 2x + (-25 x) = -23x. Iaitu, jika pekali mempunyai tanda yang berbeza dikurangkan dan hasilnya membawa tanda utama.

Tambahkan dua atau lebih polinomial dengan lebih daripada satu pemboleh ubah

Ketika datang ke polinomial dengan lebih dari satu pemboleh ubah, salah satunya dipilih untuk memerintahkannya. Sebagai contoh, katakan ia diminta untuk menambah:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

Dan:

T (x, y) = ½ x²- 6y²  - 11xy + x³dan

Salah satu pembolehubah dipilih, contohnya x untuk memerintahkan:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

Istilah yang hilang telah selesai dengan segera, mengikut mana setiap polinomial mempunyai:

R (x, y) = 0x³dan + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

Dan kedua -duanya bersedia untuk mengurangkan istilah yang sama:

0x³dan + 5x² +  8xy - 6y³  - 4y²

Boleh melayani anda: Koefisien penentuan: formula, pengiraan, tafsiran, contoh

+ x³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ x³Y + 11/2x² - 3xy - 6y³  - 10y²    = R (x, y) + t (x, y)

Latihan jumlah polinomial

- Latihan 1

Dalam jumlah polinomial seterusnya, tunjukkan istilah yang mesti masuk kosong untuk mendapatkan jumlah polinomial:

-5x⁴  + 0x³ +  2x²         + 1

x⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Penyelesaian

Untuk mendapatkan -6x⁵ istilah borang kapak diperlukan⁵, seperti itu:

A + 1+ 2 = -6

Oleh itu:

A = -6-1-2 = -9

Dan istilah yang dicari adalah:

-9x⁵

-Teruskan dengan cara yang sama untuk mencari istilah yang lain. Berikut adalah eksponen 4:

-5 + 2 + A = 10 → A = 10 + 5-2 = 13

Istilah yang hilang ialah: 13x⁴.

-Untuk kuasa x³ Segera istilah itu mestilah -9x³, Dengan cara ini pekali istilah padu ialah 0.

-Bagi kuasa persegi: A + 8 -14 = -11 → A = -11 -8 + 14 = -5 dan istilahnya ialah -5x².

-Istilah linear diperolehi oleh +8 -14 = -11 → a = -11 + 14 -8 = -5, menjadi istilah yang hilang -5x.

-Akhirnya, istilah bebas ialah: 1 -3 + a = -21 → a = -19.

- Latihan 2

Kawasan rata dikelilingi seperti yang ditunjukkan dalam angka itu. Cari ungkapan untuk:

a) perimeter dan

b) kawasannya, dari segi panjang yang ditunjukkan:

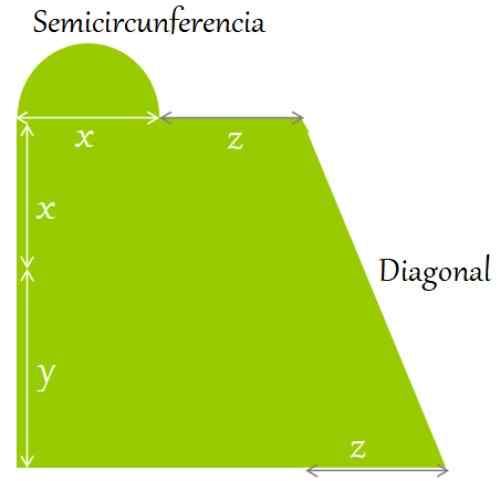Rajah 2. Kawasan rata dikelilingi oleh bentuk dan dimensi yang ditunjukkan. Sumber: f. Zapata.

Penyelesaian kepada

Perimeter ditakrifkan sebagai jumlah sisi dan kontur angka. Bermula di sudut kiri bawah, ke arah tangan jam, anda mempunyai:

Ia boleh melayani anda: isosceles trapezoid: sifat, hubungan dan formula, contoh

Perimeter = y + x + panjang separuh bulatan + z + Panjang pepenjuru + Z + z + x

Separuh bulatan mempunyai diameter sama dengan x. Oleh kerana radius adalah separuh diameter, ia harus:

Radio = x/2.

Formula untuk panjang lilitan lengkap adalah:

L = 2π x radio

Jadi:

Panjang separuh bulatan = ½. 2π (x/2) = πx/2

Bagi bahagiannya, pepenjuru dikira dengan teorem Pythagoras yang digunakan pada sisi: (x+y) yang merupakan sisi menegak dan z, yang merupakan mendatar:

Diagonal = [(x+y)² + z²]^1/2

Ekspresi ini digantikan di perimeter, untuk mendapatkan:

Perimeter = y + x + πx/2 + z + [(x + y)² + z²]^1/2+ z + x + z

Istilah yang sama dikurangkan, kerana jumlahnya memerlukan hasilnya dipermudahkan hingga maksimum:

Perimeter = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z²]^1/2 = y + (2 + π /2) x + 3z

Penyelesaian b

Kawasan yang dihasilkan adalah jumlah kawasan segi empat tepat, separuh bulatan dan segitiga yang betul. Formula untuk kawasan ini adalah:

-Rectangle: Asas x ketinggian

-Separuh bulatan: ½ π (radio)²

-Segitiga: Asas x ketinggian /2

Kawasan Rectangle

(x+y). (x+z) = x² + Xz + yx + yz

Kawasan separuh bulatan

½ π (x/2)² = π x² / 8

Kawasan segitiga

½ z (x + y) = ½ zx + ½ zy

Jumlah kawasan

Untuk mencari kawasan keseluruhan, ungkapan yang ditemui untuk setiap kawasan separa ditambah:

Jumlah kawasan = x² + Xz + yx + yz + (π x² / 8) + ½ zx + ½ zy

Dan akhirnya semua istilah yang serupa:

Jumlah kawasan = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Rujukan

1. Baldor, a. 1991. Algebra. Editorial kebudayaan Venezuela.Ke.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Matematik menyeronokkan. Menambah dan penolakan polinomial. Pulih dari: MathSisfun.com.
4. Institut Monterey. Menambah dan menolak polinomial. Pulih dari: Montereyinstitute.org.
5. UC Berkeley. Algebra polinomial. Pulih dari: matematik.Berkeley.Edu.