Jumlah Kaedah Grafik Vektor, Contoh, Latihan Selesai

The Jumlah vektor Ia adalah operasi tambahan antara vektor yang menghasilkan vektor lain. Vektor dicirikan dengan mempunyai magnitud, dan juga arah dan makna. Oleh itu, tidak mungkin, secara umum, untuk menambahkannya kerana ia akan dilakukan dengan kuantiti skalar, iaitu, menambahkan nombor.

Vektor yang diperoleh dari jumlah beberapa vektor dipanggil Hasil vektor. Dalam mekanik kita bercakap mengenai mengakibatkan daya, yang merupakan jumlah vektor dari semua daya di badan. Hasil ini bersamaan dengan set atau sistem daya.

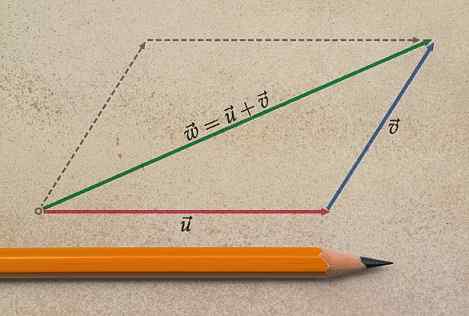
Untuk menentukan sepenuhnya jumlah vektor, perlu menunjukkan magnitud dan perpaduan, arah dan makna.

Penting untuk menyerlahkan bahawa dengan menambahkan vektor, ini mesti mewakili magnitud fizikal yang sama, oleh itu jumlah vektor adalah operasi homogen. Ini bermakna kita boleh menambah satu daya dengan yang lain, tetapi bukan kekuatan dengan anjakan, kerana hasilnya tidak bermakna.

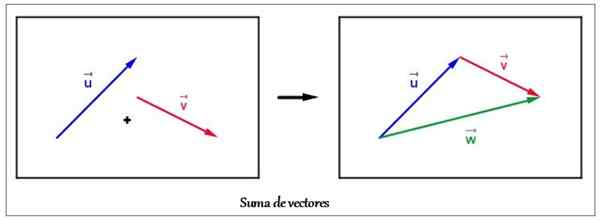
Beberapa kaedah tersedia untuk mencari vektor yang dihasilkan: Grafik dan Analisis. Untuk mencari jumlah vektor dengan kaedah grafik, ia berdasarkan perwakilan mudah untuk vektor, iaitu, segmen berorientasikan atau anak panah seperti ini:

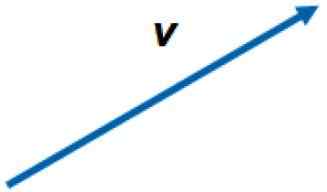Perwakilan grafik vektor dalam pesawat. Sumber: f. Zapata.

Vektor dilambangkan oleh huruf hitam dalam teks bercetak, atau dengan anak panah di atas surat, untuk membezakannya dari magnitud masing -masing atau kuantiti skalar. Contohnya, magnitud vektor v Ia semata -mata v.

[TOC]

Kaedah grafik untuk menambah vektor

Untuk menambah lebih daripada dua vektor couplet, Kaedah poligon Sama ada poligon, yang terdiri daripada memindahkan diri mereka ke setiap vektor yang ditangani. Ciri -ciri vektor adalah bahawa mereka adalah invarian mengenai terjemahan, oleh itu kita akan menggunakan harta ini untuk menubuhkan jumlah.

Boleh melayani anda: peleburan terma

Ia bermula dengan mana -mana vektor, kerana penambahan vektor adalah komutatif dan urutan penambahan tidak mengubah jumlahnya. Vektor kedua bergerak di bawah, sepadan dengan asalnya dengan akhir yang pertama.

Kemudian ia dibawa ke vektor seterusnya dan kemudian meletakkan prosedur yang sama, yang sepadan dengan asalnya dengan akhir yang sebelumnya. Kami meneruskan dengan cara ini untuk meletakkan vektor terakhir.

Vektor yang dihasilkan adalah yang menyertai asal -usul yang pertama dengan akhir percuma yang terakhir. Nama kaedah ini berasal dari angka yang hasilnya: poligon.

Contoh

Contoh Jumlah Dua Vektor dalam Pesawat Dengan Kaedah Grafik. Sumber: Wikimedia Commons

Mari kita ambil sebagai contoh jumlah dua vektor atau dan v yang ditunjukkan pada angka atas.

Bermula dengan vektor atau, Dia berpindah ke vektor v Untuk memadankan asalnya dengan akhir yang pertama. Vektor yang dihasilkan W Ia diambil dari asal atau hingga akhir v, membentuk angka tiga orang: segitiga. Itulah sebabnya dalam kes khas ini, prosedur dipanggil Kaedah Segitiga.

Perhatikan perincian penting, magnitud atau modul vektor yang dihasilkan bukanlah jumlah modul vektor tambahan. Malah, hampir selalu kurang, kecuali vektor selari.

Mari kita lihat di bawah apa yang berlaku dalam kes ini.

Kes Khas: Jumlah vektor selari

Kaedah yang diterangkan juga boleh digunakan untuk kes khas di mana vektor selari. Pertimbangkan contoh berikut:

Boleh melayani anda: Boltzmann Constant: Sejarah, Persamaan, Pengiraan, LatihanJumlah vektor selari. Sumber: f. Zapata.

Vektor ditinggalkan v Dalam kedudukan asalnya, dan bergerak ke vektor atau sedemikian rupa yang asalnya bersetuju dengan akhir  v. Sekarang vektor diambil dari asal v Dan akhir atau.

Ini adalah vektor yang dihasilkan W dan saiznya adalah jumlah saiz iklan. Arah dan arah tiga vektor adalah sama.

Vektor yang dihasilkan mempunyai modul maksimum jika penambah membentuk sudut 0º, seperti contohnya. Sekiranya vektor membentuk sudut 180º antara satu sama lain, maka vektor yang dihasilkan mempunyai modul minimum.

Contoh jumlah vektor

- Perpindahan

Pelumba basikal bergerak pertama 3 km menuju utara dan kemudian 4 km barat. Anjakan anda, yang kami panggil R, Ia mudah dijumpai dengan kaedah segitiga ditambah sistem rujukan, di mana titik kardinal ditandakan:

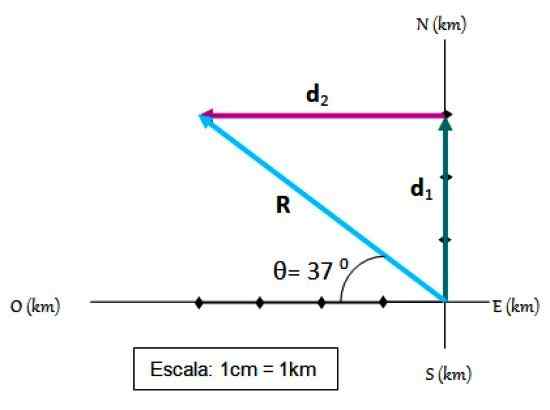Hasil daripada dua anjakan. Sumber: f. Zapata.

Langkah untuk menambah vektor

-Titik permulaan bertepatan dengan asal sistem rujukan.

-Pada paksi koordinat skala dipilih, yang dalam kes ini adalah 1 cm = 1 km

-Anjakan pertama ditarik pada skala d_1.

-Kemudian a d₁ Anjakan kedua ditarik d₂, Juga pada skala.

-Anjakan yang terhasil R Ia adalah vektor yang pergi dari asal hingga akhir d₂.

-Saiz R Ia diukur dengan peraturan lulus, mudah untuk mengesahkan bahawa r = 5.

-Akhirnya sudut itu R Bentuk dengan mendatar diukur dengan bantuan pengangkut dan ternyata menjadi θ = 37 ⁰

- Kelajuan yang dihasilkan

Seorang perenang ingin menyeberangi sungai dan untuk ini tidak ada kelajuan 6 km/j, tegak lurus ke pantai, tetapi arus yang membawa kelajuan 4 km/j menyimpangnya.

Ia dapat melayani anda: ohm: langkah rintangan, contoh dan senaman diselesaikan

Untuk mengetahui kelajuannya yang terhasil, vektor kelajuan perenang ditambah, yang telah ditarik menegak dan semasa, yang mendatar.

Mengikuti kaedah grafik kelajuan yang dihasilkan diperolehi v_R:

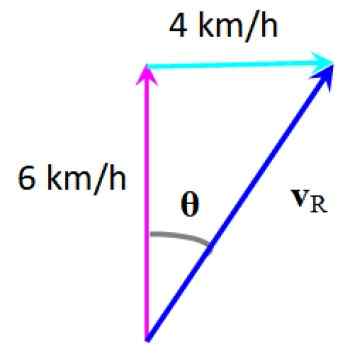Kelajuan yang dihasilkan. Sumber: f. Zapata.

Penyimpangan yang dialami oleh perenang boleh dikira oleh:

θ = arctg (4/6) = 33.Ke -7 ke kanan alamat awal anda

Besarnya kelajuannya meningkat kerana kelajuan sungai menambah vektor. Anda boleh mencari skala dengan teliti, seperti contoh sebelumnya.

Atau dengan bantuan alasan trigonometri sebanyak 33.Ke -7:

Sen 33.7 = 4/v_R

v_R = 4/ dosa 33.7th = 7.21 km/j

Latihan diselesaikan

Pada zarah, Akta Kuasa berikut, yang magnitudnya disenaraikan di bawah:

F₁= 2.5 n; F₂= 3 n; F₃= 4 n; F₄= 2.5 n

Cari daya yang dihasilkan.

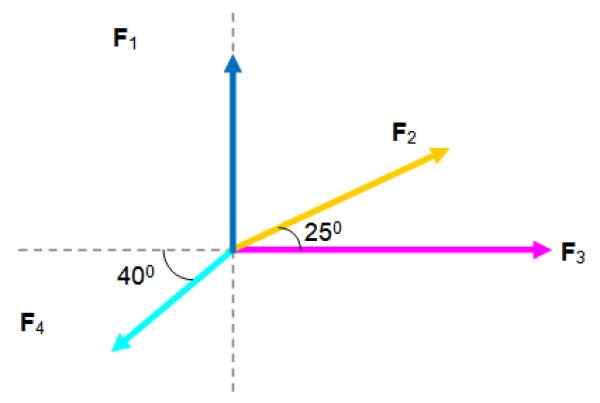Sistem Angkatan Coplanar. Sumber: f. Zapata.

Penyelesaian

Kita boleh menambah secara grafik bermula dengan mana -mana vektor, kerana jumlah vektor adalah komutatif.

Dalam angka A bermula dengan F₁. Mewujudkan skala dan dengan bantuan peraturan dan skuad vektor lain dipindahkan untuk meletakkannya satu demi satu.

Vektor F_R diarahkan dari asal F₁ hingga akhir F₄. Besarnya 5.2 N dan membentuk sudut 26.Ke -5 berkenaan dengan mendatar.

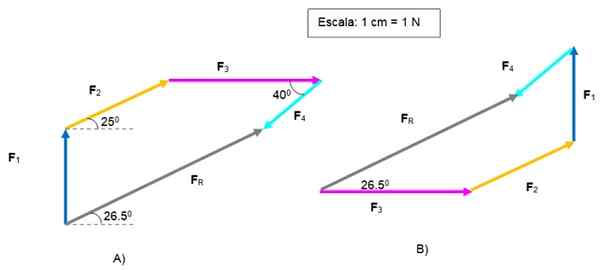Jumlah grafik vektor. Sumber: f. Zapata.

Dalam Rajah B, masalah yang sama telah diselesaikan, bermula dengan F₃ dan berakhir dengan F₄, Untuk mendapatkan yang sama F_R .

Poligon berbeza, tetapi hasilnya sama. Pembaca dapat menguji susunan vektor lagi.

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill.
2. Bedford, 2000. Ke. Mekanik untuk Kejuruteraan: Statik. Addison Wesley.
3. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB).
4. GiMbattista, a. 2010. Fizik. 2. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.