Teori set ciri, elemen, contoh, latihan

The Tetapkan teori Ia adalah cabang logik-mathematik yang bertanggungjawab untuk mengkaji hubungan antara entiti yang disebut set. Set dicirikan dengan menjadi koleksi objek yang sama. Objek ini adalah unsur -unsur set dan boleh: nombor, huruf, angka geometri, kata -kata yang mewakili objek, objek itu sendiri dan lain -lain.

Itu adalah Georg Cantor, menjelang akhir abad ke -19, yang mencadangkan set set. Sementara ahli matematik yang lain pada abad kedua puluh membuat formalisasi mereka: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel antara lain.

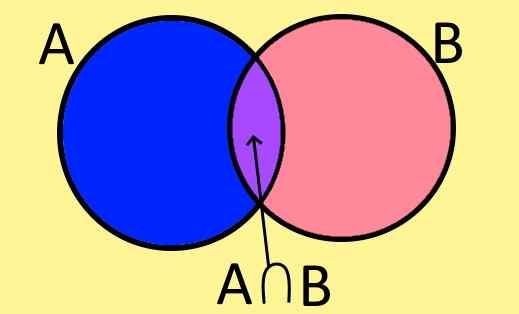
Rajah 1. Venn Diagram Set A, B dan Persimpangan mereka A⋂ B. (Huraian sendiri).

Rajah Venn adalah cara grafik mewakili satu set, dan terdiri daripada angka rata tertutup di mana unsur -unsur set itu.

Sebagai contoh, Rajah 1 menunjukkan dua set A dan B, yang mempunyai unsur -unsur yang sama, unsur -unsur yang biasa dengan A dan B. Ini membentuk satu set baru yang dipanggil set persimpangan A dan B, yang ditulis secara simbolik seperti berikut:

A ∩ B

[TOC]

Ciri -ciri

Set adalah konsep primitif kerana dalam geometri konsep titik, lurus atau rata. Tidak ada cara yang lebih baik untuk menyatakan konsep daripada menunjukkan contoh: 

Set dan dibentuk oleh warna bendera Sepanyol. Cara menyatakan set ini dipanggil oleh pemahaman. Set yang sama dan ditulis dengan lanjutan adalah:

E = merah, kuning

Dalam kes ini, merah dan kuning adalah elemen set dan. Harus diperhatikan bahawa unsur -unsur disenaraikan di antara kunci dan tidak diulang. Dalam kes bendera Sepanyol terdapat tiga jalur warna (merah, kuning, merah) dua daripadanya diulang, tetapi unsur -unsur tidak diulang apabila set dinyatakan.

Anggapkan Set V dibentuk oleh tiga huruf vokal pertama:

V = a, e, i

Kuasa V, yang dilambangkan oleh p (v) adalah set semua set yang boleh dibentuk dengan unsur -unsur v:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Jenis set

Set terhingga

Ia adalah satu set di mana unsur -unsurnya adalah angka. Contoh set terhingga adalah huruf abjad Sepanyol, vokal bahasa Sepanyol, planet sistem suria antara lain. Bilangan elemen set terhingga dipanggil kardinaliti.

Set tak terhingga

Ensemble Infinite, semua orang yang bilangan unsurnya tidak dapat ditanding.

Contoh set tak terhingga ialah set nombor semulajadi n, yang secara meluas dinyatakan seperti berikut:

Boleh melayani anda: mata coplanares: persamaan, contoh dan latihan yang diselesaikan

N = 1, 2, 3, 4, 5, .. . jelas satu set tak terhingga, kerana tidak kira berapa besar bilangan semula jadi, majoriti berikut dapat dijumpai dalam proses yang tidak berkesudahan. Jelas kardinaliti set tak terhingga adalah ∞.

Set kosong

Ia adalah set yang tidak mengandungi unsur. Set kosong V dilambangkan oleh Ø atau dengan sepasang kunci tanpa unsur di dalam:

V = = Ø.

Set kosong adalah unik, oleh itu ia mesti salah untuk mengatakan "set kosong", bentuk yang betul adalah mengatakan "set kosong".

Di antara sifat -sifat set kosong, ia adalah subset dari mana -mana set:

Ø ⊂ a

Di samping itu, jika set adalah subset set kosong, maka set ini semestinya menjadi kekosongan:

A ⊂ Ø ⇔ A = Ø

Set kesatuan

Ia dipanggil set kesatuan mana -mana set yang mengandungi satu elemen. Contohnya, set satelit semulajadi bumi adalah set unit, yang satu -satunya elemennya adalah bulan. Tetapkan b dari keseluruhan nombor lebih kecil daripada 2 dan lebih besar daripada sifar hanya mempunyai elemen 1 oleh itu ia adalah set unit.

Set binari

Set adalah binari jika hanya mempunyai dua elemen. Contohnya set x, sehingga x adalah bilangan sebenar x^2 = 2 = 2. Ini ditetapkan oleh lanjutan ditulis seperti ini:

X = --2, +√2

Set Universal

Set sejagat adalah satu set yang mengandungi set lain jenis atau sifat yang sama. Sebagai contoh, set nombor semulajadi sejagat adalah set nombor sebenar. Tetapi nombor sebenar juga universal dari nombor dan nombor rasional.

Item teras

- Hubungan antara set

Dalam set anda boleh menubuhkan beberapa jenis hubungan antara mereka dan elemen mereka. Jika dua set A dan B mempunyai unsur -unsur yang sama, di antaranya, hubungan yang sama dilambangkan seperti berikut:

Ke = B

Jika semua unsur -unsur set untuk dimiliki oleh set B, tetapi tidak semua elemen B milik A, maka di antara set ini terdapat hubungan inklusi yang dilambangkan seperti berikut:

A ⊂ b, tetapi b ⊄ a

Ungkapan sebelumnya berbunyi: A adalah subset B, tetapi B bukan subset a.

Untuk menunjukkan bahawa sesetengah atau beberapa elemen tergolong dalam satu set digunakan simbol kepunyaan ∈, contohnya untuk mengatakan bahawa elemen x atau unsur milik set A ditulis secara simbolik seperti berikut:

x ∈ A

Ya elemen dan tidak tergolong dalam set hubungan ini ditulis seperti ini:

dan ∉ a

Hubungan kepunyaan diberikan antara unsur -unsur set dan set, dengan pengecualian tunggal set kuasa, set adalah koleksi atau set semua set yang mungkin yang dapat dibentuk dengan unsur -unsur set tersebut.

Boleh melayani anda: pemfaktoran

Asume v = a, e, i, kuasa anda adalah p (v) = a, e, i, a, e, a, i, e, i, a, e, i, dalam hal ini set V menjadi elemen set p (v) dan boleh ditulis:

V ∈ P (v)

- Sifat inklusi

Harta pertama kemasukan menetapkan bahawa setiap set terkandung dalam dirinya sendiri, atau dengan kata lain, yang merupakan subset dari dirinya sendiri:

A ⊂ a

Harta lain kemasukan adalah transitiviti: jika A adalah subset B dan B pada gilirannya, ia adalah subset C, maka A adalah subset c. Simbol Hubungan Transitiviti ditulis seperti ini:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Berikut adalah gambarajah Venn yang sepadan dengan transitiviti kemasukan:

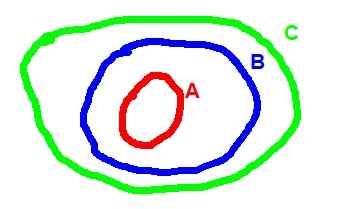Rajah 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Operasi antara set

Persimpangan

Persimpangan adalah operasi antara dua set yang menghasilkan satu set baru milik set sejagat yang sama dari dua yang pertama. Dalam erti kata itu, ia adalah operasi tertutup.

Secara simbolik, operasi persimpangan dirumuskan seperti berikut:

A⋂b = x / x∈A ^ x∈B

Contohnya adalah seperti berikut: Tetapkan huruf dalam perkataan "elemen" dan tetapkan b huruf perkataan "berulang", persimpangan antara a dan b ditulis seperti ini:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . Set sejagat A, dari B dan juga A⋂b adalah set huruf abjad Sepanyol.

Kesatuan

Kesatuan dua set adalah set yang dibentuk oleh unsur -unsur yang biasa dengan dua set dan unsur -unsur bukan umum dari dua set. Operasi kesatuan antara set dinyatakan secara simbolik seperti berikut:

A∪b = x/x∈A v x∈B

Beza

Operasi set sekurang-kurangnya set dilambangkan oleh A-B. A-B adalah set baru yang dibentuk oleh semua elemen yang ada dalam dan yang bukan milik B. Simbol ditulis seperti ini:

A - b = x/ x ∈ A ^ x ∉ b

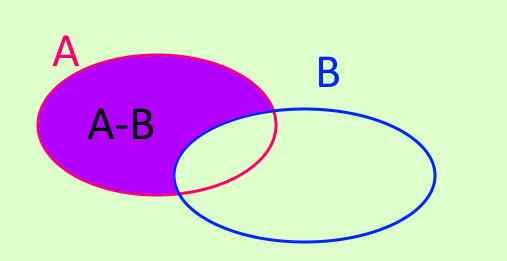Rajah 3. A - b = x/ x ∈ A ^ x ∉ b

Perbezaan simetri

Perbezaan simetri adalah operasi antara dua set di mana set yang dihasilkan terdiri daripada unsur -unsur yang tidak biasa dengan dua set. Perbezaan simetri secara simbolik diwakili seperti berikut:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Contoh

Contoh 1

Rajah Venn adalah cara grafik untuk mewakili set. Sebagai contoh, tetapkan c huruf set perkataan diwakili seperti berikut:

Contoh 2

Ia ditunjukkan di bawah melalui gambar rajah Venn bahawa, set vokal dalam perkataan "set", adalah subset dari set huruf perkataan "set".

Boleh melayani anda: persampelan kuota: kaedah, kelebihan, kekurangan, contoh

Contoh 3

Tetapkan Ñ Dari huruf abjad Sepanyol ia adalah set terhingga, set ini dengan lanjutan ditulis seperti ini:

Ñ = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z dan Kardinal adalah 27.

Contoh 4

Tetapkan V Dari vokal dalam bahasa Sepanyol ia adalah subset dari set:

V ⊂ Ñ Oleh itu ia adalah set terhingga.

Set terhingga V Cara yang dilanjutkan ia ditulis seperti ini: V = a, e, i, o, u dan kardinalitasnya adalah 5.

Contoh 5

Memandangkan set A = 2, 4, 6, 8 dan B = 1, 2, 4, 7, 9 Tentukan A-B dan B-A. 

A - B adalah unsur -unsur yang mereka tidak berada di B:

A - b = 6, 8

B - A adalah unsur -unsur B yang tidak berada dalam:

B - A = 1, 7, 9

Latihan yang diselesaikan

Latihan 1

Tulis simbolik dan juga dengan meluaskan kelopak p nombor semulajadi lebih rendah daripada 10.

Penyelesaian: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Latihan 2

Anggapkan keseluruhan yang dibentuk oleh nombor semula jadi yang menjadi faktor 210, dan set B yang dibentuk oleh sepupu nombor semula jadi lebih rendah daripada 9. Tentukan kedua -dua set dengan lanjutan dan tentukan hubungan yang ada di antara kedua -dua set tersebut.

Penyelesaian: Untuk menentukan unsur -unsur set A, anda mesti bermula dengan mencari faktor -faktor Nombor Semulajadi 210:

210 = 2 * 3 * 5 * 7

Kemudian tetapkan A ditulis:

A = 2, 3, 5, 7

Kami terus mempertimbangkan set b, iaitu sepupu lebih kecil daripada 9. 1 bukan sepupu kerana ia tidak memenuhi definisi sepupu: "Nombor adalah sepupu jika dan hanya jika ia mempunyai dua pembahagi 1 dan nombor itu sendiri". 2 adalah walaupun dan pada masa yang sama adalah sepupu kerana ia memenuhi definisi sepupu, sepupu lain lebih kecil daripada 9 adalah 3, 5 dan 7. Jadi set B adalah:

B = 2, 3, 5, 7

Oleh itu kedua -dua set adalah sama: a = B.

Latihan 3

Tentukan set yang elemen x berbeza dari x.

Penyelesaian: C = x / x ≠ x

Seperti mana -mana elemen, nombor atau objek adalah sama dengan dirinya sendiri, set c tidak boleh selain daripada set kosong:

C = Ø

Latihan 4

Menjadi set n nombor semula jadi dan z set nombor keseluruhan. Tentukan n ⋂ z y n ∪ z.

Penyelesaian: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z kerana n ⊂ z.

Rujukan

1. Garo, m. (2014). Matematik: Persamaan Kuadratik: Bagaimana Menyelesaikan Persamaan Kuadrat. Marilù Garo.
2. Haeussler, e. F., & Paul, r. S. (2003). Matematik untuk Pentadbiran dan Ekonomi. Pendidikan Pearson.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematik 1 Sep. Ambang.
4. Berharga, c. T. (2005). Kursus Matematik 3O. Progreso editorial.
5. Matematik 10 (2018). "Contoh set terhingga". Diperolehi dari: Matematik10.jaring
6. Wikipedia. Tetapkan teori. Pulih dari: Adakah.Wikipedia.com