Teorem Bernoulli

Kami menerangkan apakah teorem Bernoulli, persamaan, aplikasi dan menyelesaikan latihan

Apakah teorem Bernoulli?

Dia Teorem Bernoulli Dia menegaskan bahawa, dalam cecair yang ideal yang beredar di saluran, tenaga mekanikal per unit jumlah bendalir adalah malar di semua bahagian tiub, tanpa mengira bahawa mereka mempunyai bahagian melintang yang berlainan dan ketinggian.

Sekarang, cecair yang ideal adalah salah satu yang tidak dapat dimampatkan, jadi ketumpatannya tetap, tanpa mengira nilai tekanan.

Di samping itu, cecair yang ideal mempunyai kelikatan sifar, iaitu, tidak ada geseran antara lapisan bendalir dan tidak antara cecair dan dinding saluran.

Syarat yang tidak dapat dikesan dan kelikatan null adalah penting untuk memohon teorem Bernoulli. Ia juga perlu untuk aliran menjadi pegun, iaitu, alirannya tidak berubah dari masa ke masa.

Sebaliknya, aliran mesti laminar, jadi tidak ada pusaran atau pergolakan semasa laluan saluran.

Persamaan Bernoulli

Persamaan Bernoulli mempunyai tiga istilah, kerja yang dilakukan oleh akhbar p, tenaga kinetik dan tenaga potensi graviti untuk setiap unit cecair ketumpatan volumetrik ρ

Persamaan Bernoulli adalah:

Sebaliknya, persamaan kesinambungan menetapkan bahawa dalam cecair ideal aliran adalah tetap di semua bahagian tiub aliran. Iaitu, jumlah cecair dalam unit masa yang sama adalah sama di semua bahagian tiub.

Sekiranya alirannya q, maka:

Q = tetap

Dengan:

Q = A · V

Di mana A adalah kawasan bahagian silang tiub dan v adalah kelajuan bendalir.

Boleh melayani anda: satelit buatan

Diperhatikan bahawa di bahagian sempit tiub, cecair mesti beredar lebih cepat, kerana ia tetap malar walaupun ia berbeza -beza. Oleh itu, tenaga kinetik per unit volum lebih besar.

Oleh kerana teorem Bernoulli menetapkan bahawa tenaga mekanikal tetap di semua bahagian, di bahagian sempit tenaga kinetik yang lebih besar, tenaga berpotensi berkurangan. 

Tenaga yang berpotensi terdiri daripada tenaga graviti per unit jumlah ditambah kerja yang dilakukan oleh tekanan dalam jumlah unit, oleh itu, dengan mengurangkan tenaga berpotensi juga mengurangkan tekanan.

Ringkas.

Terma dalam persamaan Bernoulli

1) Kerja yang dilakukan oleh tekanan per unit jumlah 

Di bahagian bahagian silang kawasan ke, Cecair bergerak jumlah s, Kerana tekanan p yang menghasilkan daya f = p angani a.

Kerja yang dilakukan secara paksa adalah:

F

Oleh kerana produk a ⋅ s mewakili jumlah yang dipindahkan, maka kerja yang dilakukan per unit jumlahnya sepadan dengan nilai p dalam bahagian yang dipertimbangkan.

2) Tenaga kinetik jumlah unit cecair

Oleh kerana cecair tidak dapat dikompresikan, ketumpatannya mempunyai nilai tetap yang dipanggil ρ.

Apabila bendalir beredar melalui seksyen rentas seksyen A, menggerakkan jumlah s dalam masa t, kadar aliran adalah:

Ia boleh melayani anda: Undang -undang Termodinamik Kedua: Formula, Persamaan, Contoh

v = s/t

Dan tenaga kinetik bahagian cecair tersebut dikira oleh:

K = ½ ρ (a ⋅ s) v²

Tetapi jika jumlah yang dipindahkan (a ⋅ s) adalah unit, maka istilah tenaga kinetik akan diberikan oleh ½ ρ v².

3) Tenaga potensi graviti jumlah unit bendalir pada ketinggian h 

Untuk bahagian cecair doh m dan ketinggian h Mengenai tahap rujukan tertentu, tenaga graviti diberikan oleh:

U = m ⋅ g ⋅ h

Jika adunan m Ia sepadan dengan bahagian cecair kesatuan, maka jisim bahagian sepadan ρ, Jadi tenaga berpotensi akan ρaraan g. H.

Aplikasi Teorem Bernoulli

Sokongan aerodinamik

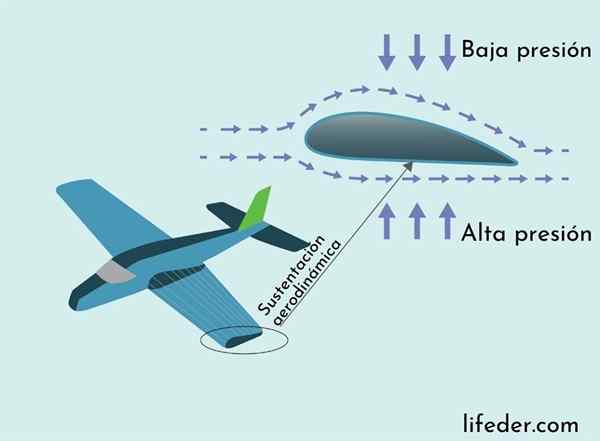Sokongan aerodinamik dijelaskan oleh teorem Bernoulli

Daya yang menghalang kapal terbang dari penerbangan ke runtuh adalah daya sokongan aerodinamik. Daya sokongan bersih diarahkan secara menegak dan bertindak di sepanjang sayap kapal terbang. Asalnya dijelaskan melalui teorem Bernoulli.

Sayap kapal terbang mempunyai bahagian silang dengan lengkung yang lebih panjang di bahagian atas dan lebih pendek di bahagian bawah. Ini menjadikan laluan udara berhampiran permukaan sayap di bahagian atas, jadi udara mengalir lebih cepat di atas sayap daripada bahagian bawah. 

Sebagai akibat daripada teorem Bernoulli, tekanan udara di bahagian atas sayap beredar kurang dari di bahagian bawah, mengakibatkan daya yang dikenakan oleh perbezaan tekanan diarahkan ke atas, menyokong berat pesawat, mengikutnya boleh dilihat dalam gambar berikut.

Ia boleh melayani anda: Fizik semasa orang Yunani (Antige Greece)

Pelancaran bola dan bola dengan kesan lengkung

Dalam beberapa sukan seperti bola sepak, besbol dan cricke, pemain berpengalaman tahu bagaimana. Adalah apa yang dipanggil Pelancaran Kesan.

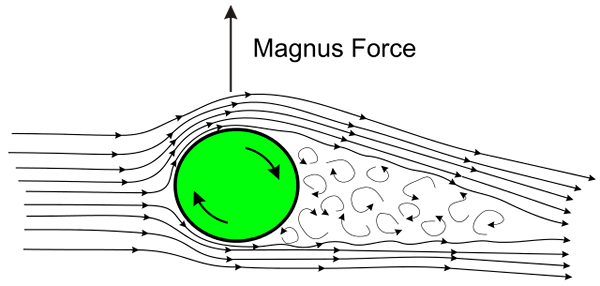Ilustrasi Kesan Magnus. Sumber: Wikimedia Commons

Kesannya berlaku apabila bola atau bola beralih dengan cepat semasa bergerak melalui udara. Putaran menyebabkan udara ke permukaan bola diseret olehnya dalam dua arah yang bertentangan, satu yang memihak kepada arah terjemahan dan, di sisi lain, terhadap arah anjakan.

Akibat seretan udara, kawasan tekanan rendah dihasilkan pada wajah bola dan di seberang tekanan tekanan tinggi, menghasilkan daya bersih yang mengalihkan trajektori semula jadi bola.

Penjelasan fenomena ini yang dikenali sebagai Kesan Magnus Ia terletak tepat di teorem Bernoulli: di mana bendalir beredar dengan cepat tekanan rendah, dan di sebelah tempat tekanan beredar perlahan.

Latihan diselesaikan

Tiub mendatar mempunyai bahagian kawasan a₁ = 40 sentimeter persegi dan seksyen lain bahagian kawasan a₂ empat kali lebih rendah. Jika aliran air adalah 6 l/s, tentukan perbezaan tekanan dan perbezaan ketinggian dalam tiub menegak.

Penyelesaian 

Bermula dari persamaan aliran, yang nilainya adalah q = 6 l/s:

Q = A · V

Anda perlu kelajuan di bahagian lebar adalah 1.5 m/s dan di regangan sempit 6 m/s.

Kemudian, memohon dan memadankan persamaan Bernoulli pada peregangan yang luas dan sempit, perbezaan tekanan 1700 PA diperolehi, yang sepadan dengan perbezaan ketinggian dalam tiub menegak 1.72 meter.