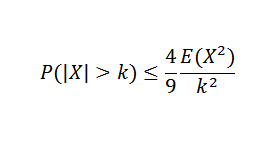Teorem Chebyshov iaitu, aplikasi dan contoh

Dia Teorem Chebyshov (atau ketidaksamaan Chebyshov) adalah salah satu hasil klasik yang paling penting dari teori kebarangkalian. Ia membolehkan menganggarkan kebarangkalian peristiwa yang diterangkan dari segi pembolehubah rawak x, dengan memberikan kita tahap yang tidak bergantung kepada pengedaran pemboleh ubah rawak tetapi pada varians x.

Teorem ini dipanggil untuk menghormati matematik Rusia.

Ketidaksamaan ini, atau yang disebabkan oleh ciri -ciri mereka dipanggil ketidaksamaan Chebyshov, kebanyakannya digunakan untuk menghampiri kebarangkalian dengan cara mengira tahap.

Apakah teorem Chebyshov?

Dalam kajian teori kebarangkalian, ia berlaku bahawa jika fungsi pengedaran pembolehubah rawak x diketahui, nilai yang diharapkan dapat dikira - atau harapan matematik dan (x) - dan variansnya var (x), selagi ini Jumlah wujud. Walau bagaimanapun, timbal balik tidak semestinya benar.

Iaitu, mengetahui e (x) dan var (x) tidak semestinya memperoleh fungsi pengedaran x, jadi kuantiti seperti p (| x |> k) untuk beberapa k> 0, sangat sukar diperoleh. Tetapi terima kasih kepada ketidaksamaan Chebyshov, mungkin untuk menganggarkan kebarangkalian pemboleh ubah rawak.

Teorem Chebyshov memberitahu kita bahawa jika kita mempunyai pembolehubah rawak x pada ruang sampel dengan fungsi kebarangkalian p, dan jika k> 0, maka:

Boleh melayani anda: acutangle triangle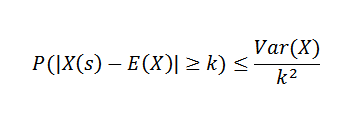

Aplikasi dan contoh

Di antara banyak aplikasi yang dimiliki oleh teorem Chebyshov, yang berikut boleh disebutkan:

1. Had kebarangkalian

Ini adalah aplikasi yang paling biasa dan digunakan untuk memberikan tahap atas untuk p (| x-e (x) | ≥K) di mana k> 0, hanya dengan varians dan harapan pembolehubah rawak x, tanpa mengetahui fungsi kebarangkalian.

Contoh 1

Katakan bilangan produk yang dibuat dalam syarikat selama seminggu adalah pemboleh ubah rawak dengan purata 50.

Sekiranya diketahui bahawa varians seminggu pengeluaran adalah sama dengan 25, maka apa yang dapat kita katakan tentang kebarangkalian bahawa minggu ini pengeluaran berbeza dengan lebih dari 10 hingga rata -rata?

Penyelesaian

Menerapkan ketidaksamaan Chebyshov kita perlu:

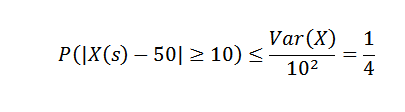
Dari ini kita dapat memperoleh kebarangkalian bahawa dalam minggu pengeluaran bilangan item melebihi lebih dari 10 hingga purata adalah paling 1/4.

2. Demonstrasi teorema had

Ketidaksamaan Chebyshov memainkan peranan penting dalam menunjukkan teorem had yang paling penting. Sebagai contoh kita mempunyai yang berikut:

Undang -undang yang lemah dari jumlah besar

Undang -undang ini menetapkan bahawa diberikan penggantian x1, x2, ..., xn, ... pembolehubah rawak bebas dengan pengedaran purata yang sama e (xi) = μ dan varians var (x) = σ², dan sampel purata yang diketahui:

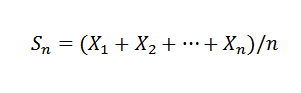
Jadi untuk k> 0 anda mesti:

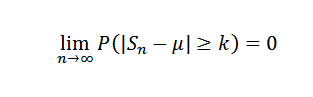
Atau setara:

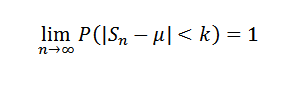
Demonstrasi

Pertama kita perhatikan perkara berikut:

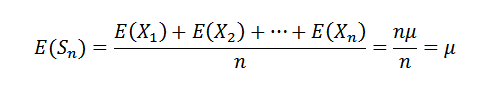
Sebagai x1, x2, ..., xn adalah bebas, ia mengikutinya:

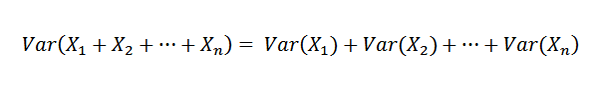
Oleh itu, adalah mungkin untuk mengesahkan perkara berikut:

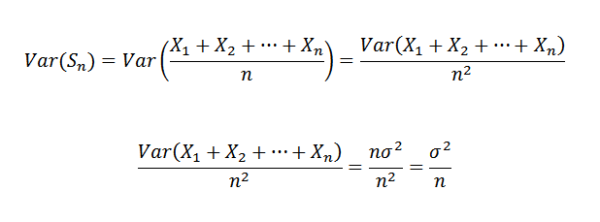
Kemudian, menggunakan teorem Chebyshov yang anda perlu:

Ia boleh melayani anda: Fungsi Trigonometrik: Asas, Dalam Plane Cartesian, Contoh, Latihan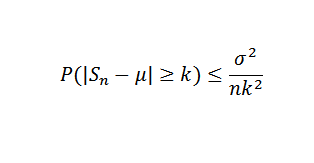

Akhir.

Harus diingat bahawa ujian ini hanya dilakukan untuk kes di mana terdapat varians XI; iaitu, ia tidak menyimpang. Oleh itu kita melihat bahawa teorem selalu benar jika e (xi) wujud.

Teorem Had Chebyshov

Jika x1, x2, ..., xn, ... ia adalah penggantian pembolehubah rawak bebas sehingga terdapat beberapa C0:

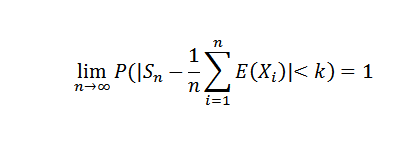
Demonstrasi

Oleh kerana penggantian variasi terhad, kita mempunyai var (sn) ≤ c/n, untuk semua n semula jadi n. Tetapi kita tahu bahawa:

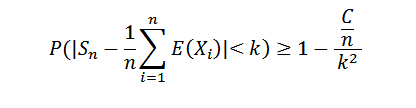
Membuat N ke Infinity, ia adalah seperti berikut:

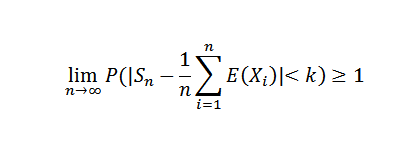
Sebagai kebarangkalian tidak dapat melebihi nilai 1, hasil yang diinginkan diperolehi. Akibat dari teorem ini kita dapat menyebutkan kes tertentu Bernoulli.

Sekiranya percubaan diulang secara bebas dengan dua hasil yang mungkin (kegagalan dan kejayaan), di mana P adalah kebarangkalian kejayaan dalam setiap eksperimen dan x adalah pembolehubah rawak yang mewakili bilangan kejayaan yang diperoleh, maka bagi setiap k> 0 anda perlu:

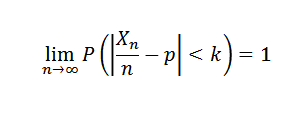
3. Saiz sampel

Dari segi varians, ketidaksamaan Chebyshov membolehkan kita mencari saiz sampel yang mencukupi untuk memastikan kebarangkalian bahawa | purata.

Tepatnya, sama ada x1, x2, ... xn Sampel pembolehubah rawak bebas saiz n dan anggap bahawa e (xi) = μ dan variansnya σ². Oleh itu, kerana ketidaksamaan Chebyshov anda perlu:

Boleh melayani anda: Nombor Euler atau Nombor E: Berapa OK, Properties, Aplikasi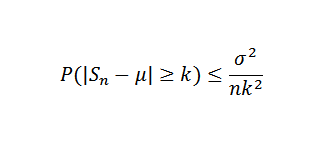

Sekarang δ> 0 tetap. Kita mesti:

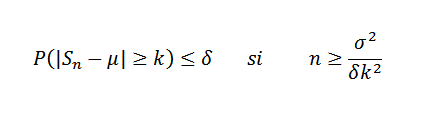
Contoh

Katakan bahawa x1, x2, ... xn adalah sampel pembolehubah rawak bebas dengan pengedaran Bernoulli, supaya mereka mengambil nilai 1 dengan kebarangkalian p = 0.5.

Apa yang sepatutnya menjadi saiz sampel untuk memastikan kebarangkalian perbezaan antara aritmetik min SN dan nilai yang dijangkakan (yang melebihi lebih daripada 0.1), kurang daripada atau sama dengan 0.,01?

Penyelesaian

Kita perlu (x) = μ = p = 0.5 dan apa var (x) = σ²= P (1-p) = 0.25. Untuk ketidaksamaan Chebyshov, untuk mana -mana k> 0 kita perlu:

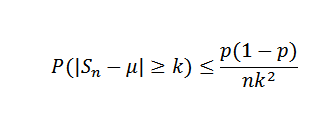
Sekarang, mengambil k = 0.1 dan δ = 0.01, anda perlu:

Dengan cara ini disimpulkan bahawa saiz sampel sekurang -kurangnya 2500 diperlukan untuk memastikan kebarangkalian peristiwa | sn - 0.5 |> = 0.1 adalah kurang daripada 0.01.

Ketidaksamaan jenis Chebyshov

Terdapat pelbagai ketidaksamaan yang berkaitan dengan ketidaksamaan Chebyshov. Salah satu yang paling terkenal ialah ketidaksamaan Markov:

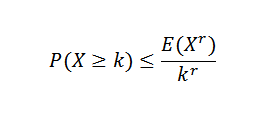
Dalam ungkapan ini x ia adalah pemboleh ubah rawak bukan negatif dengan k, r> 0.

Ketidaksamaan Markov boleh mengambil bentuk yang berbeza. Sebagai contoh, sama ada dan pemboleh ubah rawak bukan negatif (jadi p (y> = 0) = 1) dan anggap bahawa e (y) = μ ada. Katakan juga bahawa (e (y))^r= μ_r Ada untuk beberapa integer r> 1. Jadi:

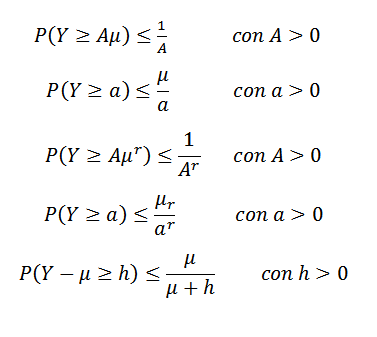
Ketidaksamaan lain ialah Gauss, yang memberitahu kita bahawa diberi pemboleh ubah rawak x unimodal dengan fesyen pada sifar, kemudian untuk k> 0,