Teorem Penjelasan Steiner, Aplikasi, Latihan

Dia Teorem Steiner, juga dikenali sebagai Teorem paksi selari, Ia membolehkan untuk menilai momen inersia badan yang dilanjutkan, sekitar paksi yang selari dengan yang lain yang melewati pusat jisim objek.

Ia ditemui oleh matematik Switzerland_Cm Momen inersia objek berkenaan dengan paksi yang melewati CM dan I Pusat Massa_z Momen inersia berkenaan dengan paksi selari yang lain untuk ini.

Rajah 1. Pintu segi empat tepat menghidupkan kegembiraannya mempunyai momen inersia yang dapat dikira dengan menggunakan teorem Steiner. Sumber: Pixabay.

Dikenali jarak d yang memisahkan kedua -dua paksi dan jisim m dari badan yang dipersoalkan, momen inersia berkenaan dengan paksi penyamaran adalah:

Yo_z = I_Cm + Md²

Momen inersia menunjukkan betapa mudahnya bagi objek untuk berputar di sekitar paksi tertentu. Ia tidak hanya bergantung pada badan badan, tetapi bagaimana ia diedarkan. Atas sebab ini ia juga dikenali sebagai Inersia putaran, Menjadi unit anda dalam sistem KG antarabangsa . m².

Teorem menunjukkan bahawa momen inersia Yo_z Selalunya lebih besar daripada momen inersia Yo_Cm dalam jumlah yang diberikan oleh M.D².

[TOC]

Aplikasi

Sebagai objek dapat berputar di sekitar banyak paksi, dan dalam jadual biasanya hanya momen inersia mengenai paksi yang melewati centroid, teorem Steiner memudahkan pengiraan apabila ia perlu memutar badan pada gandar pada gandar yang tidak bertepatan dengan ini.

Boleh melayani anda: Pergerakan Rectilinear: Ciri, Jenis dan Contoh

Sebagai contoh, pintu biasanya tidak berputar di sekitar paksi yang melalui pusat jisimnya, tetapi berkenaan dengan paksi sisi, di mana engsel mematuhi.

Apabila mengetahui momen inersia adalah mungkin untuk mengira tenaga kinetik yang berkaitan dengan putaran pada paksi ini. Yeah K adalah tenaga kinetik, Yo saat inersia di sekitar paksi yang dipersoalkan dan Ω Halaju sudut dipenuhi:

K = ½ i.Ω²

Persamaan ini sangat serupa dengan formula tenaga kinetik yang sangat biasa untuk objek massa M bergerak dengan kelajuan v:  K = ½ m.v². Dan adakah momen inersia atau inersia putaran Yo memainkan giliran peranan yang sama dengan adunan M Dalam terjemahan.

Demonstrasi Teorem Steiner

Momen inersia objek lanjutan ditakrifkan sebagai:

I = ∫r² DM

Di mana DM Ia adalah jisim jisim yang sangat kecil dan r Ia adalah jarak antara DM dan paksi putaran z. Dalam Rajah 2 paksi ini melintasi pusat jisim cm, namun ia boleh menjadi sesiapa pun.

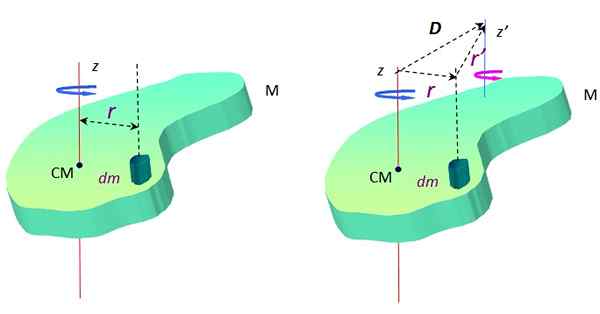Rajah 2. Objek dilanjutkan dalam putaran sekitar dua paksi selari. Sumber: f. Zapata.

Sekitar paksi lain  z ', Momen inersia adalah:

Yo_z= ∫ (R ')² DM

Sekarang, menurut segitiga yang dibentuk oleh vektor D, r dan R ' (Lihat Rajah 2 di sebelah kanan), terdapat jumlah vektor:

r + R ' = D   → R ' = D - r

Tiga vektor berada di dalam satah objek yang boleh menjadi Xy. Asal sistem koordinat (0.0) dipilih dalam CM untuk memudahkan pengiraan yang mengikuti.

Dengan cara ini modul persegi vektor R ' adalah:

Boleh melayani anda: biofizik: sejarah, kajian, aplikasi, konsep, kaedah apa

(R ')² = (D_x- r_x)² +(D_dan - r_dan)² =

= D_x² + D_dan² +r_x² + r_dan2 -2d_xr_x - 2 d_danr_dan =

= D² + r²  - 2d_xr_x - 2 d_danr_dan

Sekarang perkembangan ini digantikan dengan integral momen inersia i_z dan juga definisi ketumpatan dm = ρ digunakan.DV:

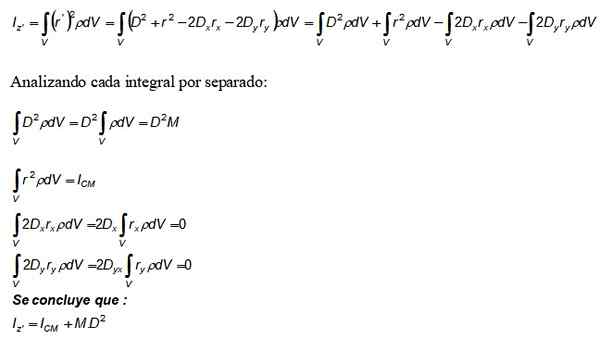
Istilah m. D² yang muncul dalam teorem Steiner berasal dari integral pertama, yang kedua adalah momen inersia mengenai paksi yang melalui cm.

Bagi pihaknya, integral ketiga dan keempat bernilai 0, kerana dengan definisi mereka menjadi kedudukan CM, yang telah dipilih sebagai asal sistem koordinat (0.0).

Latihan yang diselesaikan

-Latihan diselesaikan 1

Pintu segi empat tepat Rajah 1 mempunyai jisim 23 kg, 1.30 lebar dan tinggi 2.10 m. Tentukan momen inersia pintu mengenai paksi yang melalui kegembiraan, dengan mengandaikan bahawa pintu itu nipis dan seragam.

Rajah 3. Skim untuk contoh yang diselesaikan 1. Sumber: Pixabay yang diubahsuai.

Penyelesaian

Dari jadual momen inersia, untuk plat segi empat tepat m dan dimensi ke dan b, Momen inersia berkenaan dengan paksi yang melewati pusat jisimnya ialah: i_Cm = (1/12)M(ke² + b²).

Pintu homogen akan diandaikan (pendekatan, kerana pintu angka mungkin tidak begitu banyak). Dalam kes ini, pusat jisim melalui pusat geometri. Dalam Rajah 3, paksi yang melalui pusat jisim telah ditarik dan juga selari dengan paksi yang melewati kegembiraan.

Yo_Cm = (1/12) x 23 kg x (1.30²+2.10²) m² = 11.7 kg.m²

Boleh melayani anda: apa itu geoid?

Memohon Teorem Steiner untuk paksi putaran hijau:

I = i_Cm + Md² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Latihan diselesaikan 2

Cari momen inersia batang homogen nipis apabila ia berkisar dengan paksi yang melewati salah satu hujungnya, lihat angka. Adakah ia lebih besar atau kurang dari momen inersia apabila ia berkisar di pusatnya? Kerana?

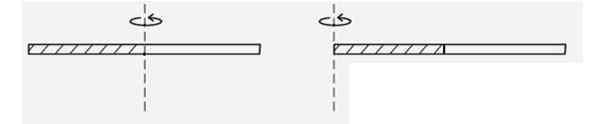Rajah 4. Skim untuk contoh yang diselesaikan 2. Sumber: f. Zapata.

Penyelesaian

Menurut momen inersia, saat inersia Yo_Cm batang adunan yang nipis M dan panjang L adalah: Yo_Cm = (1/12) ml²

Dan Teorem Steiner menyatakan bahawa apabila ia diputar di sekitar paksi yang melewati satu hujung d = l/2 kekal:

I = i_Cm + Md² = (1/12) ml² + M (l/2)² = (1/3) ml²

Sudah tua.

Pengaruh jarak ke paksi putaran tidak linear, tetapi kuadrat. Jisim yang dua kali jarak yang lain akan mempunyai momen inersia berkadar dengan (2d)² = 4d².

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 313-340.
2. Georgia State University. Gerakan putaran. Pulih dari: Phys.Nthu.Edu.TW.
3. Teorem paksi selari. Pulih dari: Hyperphysics.Phy-Astr.GSU.Edu.
4. Rex, a. 2011. Asas Fizik. Pearson. 190-200.
5. Wikipedia. Teorem paksi selari. Diperoleh dari: dalam.Wikipedia.org