Teorem Thévenin Apa yang terdiri, aplikasi dan contoh
- 4317
- 1027
- Horace Gulgowski
Dia Teorem Thévenin Ia menyatakan bahawa litar dengan terminal a dan b dapat digantikan dengan setara yang terdiri daripada sumber dan rintangan siri, yang nilai -nilainya memberikan perbezaan potensi yang sama antara a dan b dan impedans yang sama seperti litar asal.
Teorem ini dikeluarkan pada tahun 1883 oleh jurutera Perancis Léon Charles Thévenin, tetapi ia mendakwa bahawa dia dinyatakan tiga puluh tahun sebelum oleh ahli fizik Jerman Hermann von Helmholtz.
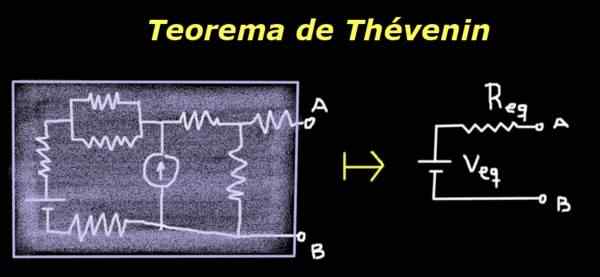
Rajah 1. Teorem Thévenin. Sumber: Diri Diri Kegunaannya terletak pada hakikat bahawa, walaupun litar asal adalah kompleks atau tidak diketahui, untuk tujuan beban atau impedans yang diletakkan di antara terminal A dan B, litar bersamaan mudah dari Thévenin berkelakuan dengan cara yang sama.
[TOC]
Bagaimana langkah voltan bersamaan dengan langkah dikira?
Voltan atau perbezaan potensi litar yang setara boleh diperolehi dengan cara berikut:
- Secara eksperimen
Mendapatkan voltan yang setara dengan thévenin
Jika ia adalah peranti atau peralatan yang berada dalam "kotak hitam", perbezaan potensi antara terminal a dan b dengan voltmeter atau osiloskop diukur. Sangat penting bahawa tiada beban atau impedans antara terminal a dan b diletakkan.
Voltmeter atau osiloskop tidak mewakili sebarang beban untuk terminal, kerana kedua -dua pasukan mempunyai impedans yang sangat besar (idealnya tak terhingga) dan akan seolah -olah terminal A dan B tanpa beban. Voltan atau voltan yang diperoleh dengan cara ini adalah ketegangan yang setara dengan thévenin.
Memperoleh impedans yang setara dengan thévenin
Untuk mendapatkan impedans yang setara dari pengukuran eksperimen, rintangan yang diketahui di antara terminal A dan B diletakkan dan penurunan voltan atau isyarat voltan dengan osiloskop diukur.
Dari kejatuhan voltan dalam rintangan yang diketahui di antara terminal, arus yang beredar melaluinya dapat diperoleh.
Produk arus yang diperolehi dengan rintangan bersamaan ditambah dengan penurunan voltan yang diukur dalam rintangan yang diketahui adalah sama dengan voltan bersamaan thévenin yang sebelumnya diperolehi. Dari kesamaan ini, impedans bersamaan thévenin dibersihkan.
- Menyelesaikan litar
Pengiraan voltan bersamaan Thévenin
Pertama, sebarang beban atau impedans terminal A dan B diputuskan.
Seperti litar yang diketahui, undang -undang meshes atau kirchhoff digunakan untuk mencari ketegangan di terminal. Ketegangan ini akan bersamaan dengan Thévenin.
Boleh melayani anda: Gunung Olympus (Marikh)Pengiraan impedans bersamaan Thévenin
Untuk mendapatkan impedans yang setara, kami meneruskan ke:
- Gantikan sumber voltan litar asal dengan pendek "sifar impedans" dan sumber litar asal untuk terbuka "impedans tak terhingga".
- Maka impedans yang setara dikira berikutan peraturan impedans dan impedans siri selari.
Aplikasi Teorem Thévenin (Bahagian I)
Kami akan menggunakan teorem Thévenin untuk menyelesaikan beberapa litar. Pada bahagian pertama ini kita menganggap litar yang hanya mempunyai sumber dan rintangan ketegangan.
Contoh 1 (Pengiraan langkah voltan bersamaan dengan langkah)
Rajah 2 menunjukkan litar yang berada di dalam kotak langit yang mempunyai dua bateri kuasa elektromotor v1 dan v2 masing -masing dan rintangan R1 dan R2, litar mempunyai terminal a dan b yang boleh disambungkan.
Rajah 2. Contoh 1 Teorem Thévenin. Sumber: Diri Diri Objektifnya adalah untuk mencari litar bersamaan thévenin, iaitu, menentukan nilai VT dan RT litar bersamaan. Gunakan nilai berikut: v1 = 4v, v2 = 1v, r1 = 3Ω, r2 = 6Ω dan r = 1Ω.
Langkah demi langkah
Langkah 1
Kami akan menentukan voltan di terminal a dan b apabila mereka tidak meletakkan beban.
Langkah 2
Litar yang perlu diselesaikan terdiri daripada satu mesh yang mana arus yang saya beredar yang telah kami ambil secara positif dalam mengikut arah jam.
Langkah 3
Kami mengembara mesh bermula dengan sudut kiri bawah. Laluan ini membawa kepada persamaan berikut:
V1 - i*r1 - i*r2 - v2 = 0
Langkah 4
Kami membersihkan arus mesh saya dan dapatkan:
I = (v1 -v2) / (r1 +r2) = (4v - 1v) / (3Ω +6Ω) = ⅓ a
Langkah 5
Dengan arus mesh kita dapat menentukan perbezaan voltan atau voltan antara a dan b, iaitu:
Vab = v1 - i * r1 = 4v - ⅓ a * 3Ω = 3v
Iaitu voltan setara Thevenin ialah: VT = 3V.
Langkah 6 (rintangan bersamaan Thévenin)
Kami kini terus mengira rintangan setara Thévenin, yang mana dan seperti yang dikatakan sebelum ini, sumber voltan digantikan oleh kabel.
Dalam hal ini, kita hanya mempunyai dua rintangan selari, jadi rintangan setara Thévenin adalah:
Rt = (r1 * r2) / (r1 + r2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Contoh 1b (arus semasa menggunakan setara thévenin)
Sambungkan sebagai beban ke terminal a dan b rintangan r = 1Ω ke litar bersamaan dan cari arus yang beredar melalui beban tersebut.
Boleh melayani anda: Pergerakan Rectilinear: Ciri, Jenis dan ContohPenyelesaian
Apabila rintangan r disambungkan ke litar setara Thevenin terdapat litar mudah yang terdiri daripada sumber VT rintangan siri dalam siri dengan rintangan r r.
Kami akan memanggil arus yang beredar melalui beban R, supaya persamaan mesh seperti ini:
Vt - ic* rt - ic* r = 0
Dari mana ia mengikuti bahawa IC diberikan oleh:
Ic = vt / (rt + r) = 3v / (2Ω + 1Ω) = 1 a
Pengesahan Teorem Thévenin
Untuk mengesahkan bahawa teorem Thévenin dipenuhi, sambungkan r ke litar asal dan cari arus yang beredar dengan menggunakan undang -undang jejaring ke litar yang dihasilkan.
Litar yang dihasilkan kekal dan persamaan meshnya adalah seperti yang ditunjukkan dalam angka berikut:
Rajah 3. Arus mesh. (Huraian sendiri) Menambah persamaan mesh, adalah mungkin untuk mencari i1 semasa mesh bergantung pada i2 semasa. Kemudian ia digantikan dalam persamaan mesh kedua dan ada persamaan dengan i2 sebagai satu -satunya yang tidak diketahui. Jadual berikut menunjukkan operasi.
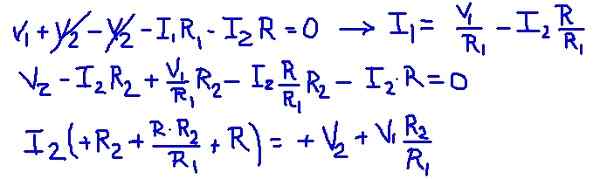Rajah 4. Perincian operasi. (Huraian sendiri) Kemudian nilai rintangan dan voltan sumber diganti, memperoleh nilai berangka arus mesh i2.
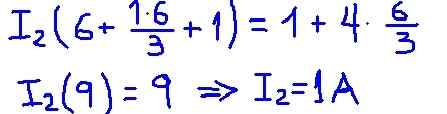Rajah 5. Terperinci hasil. (Huraian sendiri) Aliran mesh i2 adalah arus yang beredar melalui rintangan beban r dan nilai yang ditemui dari 1 A sepenuhnya bertepatan dengan apa yang sebelumnya dijumpai dengan litar bersamaan Thévenin.
Permohonan Teorem Thévenin (Bahagian II)
Di bahagian kedua ini, teorem Thévenin akan digunakan dalam litar yang mempunyai sumber ketegangan, sumber dan rintangan semasa.
Contoh 2a (rintangan bersamaan Thévenin)
Objektifnya adalah untuk menentukan litar bersamaan thévenin sepadan dengan litar angka berikut, apabila terminal tanpa rintangan 1 ohmio, maka rintangan diletakkan dan arus arus ditentukan oleh yang sama.
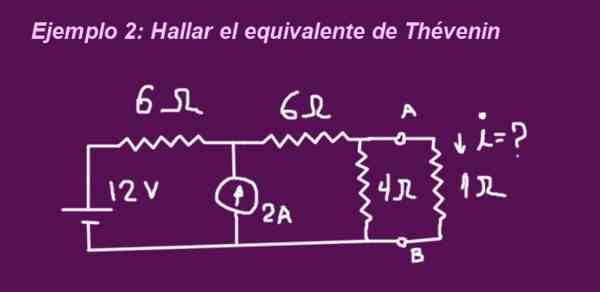Rajah 6. Contoh 2 litar. (Huraian sendiri) Penyelesaian
Untuk mencari rintangan yang setara, rintangan beban dikeluarkan (dalam kes ini 1 ohmio). Di samping itu, sumber voltan digantikan oleh litar pintas dan sumber semasa dengan litar terbuka.
Dengan cara ini, litar yang mana rintangan bersamaan akan dikira adalah yang ditunjukkan di bawah:
Boleh melayani anda: Boltzmann Constant: Sejarah, Persamaan, Pengiraan, Latihan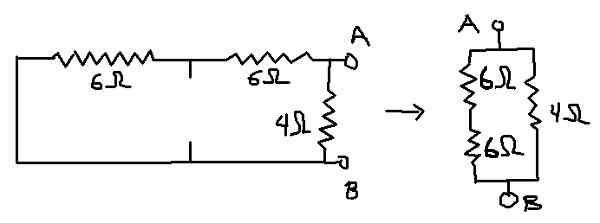
Rajah 7. Perincian untuk pengiraan rintangan bersamaan (penghuraian sendiri) Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω yang merupakan rintangan setara Thevenin (RTH).
Contoh 2b
Kirakan voltan setara Thévenin.
Penyelesaian
Untuk mengira voltan yang setara dari thévenin kita menganggap litar berikut, di mana kita akan meletakkan arus dalam i1 dan i2 di cawangan yang ditunjukkan dalam angka berikut:
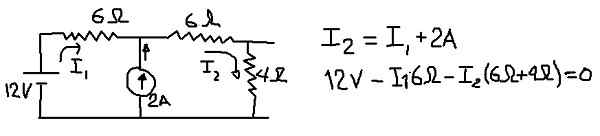Rajah 8. Perincian untuk pengiraan ketegangan Thévenin. (Huraian sendiri) Dalam angka sebelumnya, persamaan nod semasa dan persamaan ketegangan ditunjukkan apabila mesh luaran dilalui. Dari kedua persamaan i1 semasa dibersihkan:
I1 = 2 - i2*(5/3)
Persamaan ini digantikan dalam persamaan nod:
I2 = 2 - (5/3) i2 + 2 ===> i2 (8/3) = 4 ===> i2 = 12/8 = 1.5 a
Ini bermakna penurunan ketegangan dalam rintangan 4 ohm adalah 6 volt.
Singkatnya, ketegangan Thévenin adalah vth = 6 v.
Contoh 2c
Cari litar setara Thevenin dan semasa dalam rintangan beban.
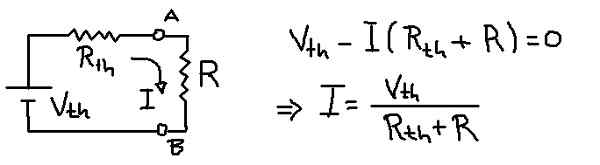Rajah 9. Semasa dalam beban dengan setaraf thévenin. (Huraian sendiri) Penyelesaian
Angka sebelumnya menunjukkan litar bersamaan thévenin dengan rintangan beban r. Dari persamaan voltan dalam mesh arus saya yang beredar melalui rintangan beban r disimpulkan.
I = vth / (rth + r) = 6v / (3Ω + 1Ω) = 1.5 a
Permohonan Teorem Thévenin (Bahagian III)
Di bahagian ketiga aplikasi teorem Thévenin, litar semasa berselang -seli mengandungi sumber voltan bergantian, kondensor, induktansi dan rintangan dianggap.
Contoh 3
Matlamatnya adalah untuk mencari litar thévenin yang setara dengan litar berikut:
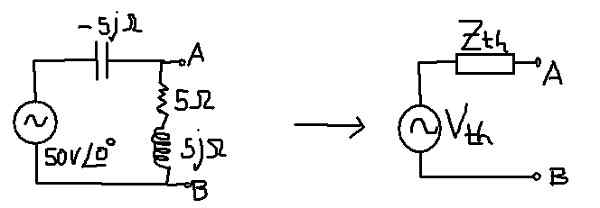Rajah 10. Thévenin dalam litar semasa berselang. (Huraian sendiri) Penyelesaian
Impedans bersamaan sepadan dengan kondensor selari dengan kombinasi siri rintangan dan induktansi.
Kebalikan dari impedans yang setara diberikan oleh:
Zeq^-1 = (-5j)^-1 + (5 + 5j)^-1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3/ 10 j) mho
Dan impedans yang setara akan menjadi:
Zeq = (1 - 3 j) ohm
Arus kompleks saya dapat disimpulkan dari persamaan mesh:
50V ♦0 - I (-5 J + 5 + 5j) = 50V utan0 - i*5 = 0 ===> i = 10a ∠0
Sekarang penurunan voltan dalam rintangan ditambah induktansi dikira, iaitu ketegangan VAB yang akan menjadi ketegangan yang setara dengan thévenin:
VAB = I * (5 + 5 J) Ω = 10A ∠0 * 5Ω akap
Dalam kata lain
Rujukan
- Tutorial Elektronik, Teorem Thevenin. Pulih dari: elektronik-tormales.WS
- Soalan dan Jawapan Teori Rangkaian. Teorem Thevenin. Pulih dari: sanfoundry.com
- Teorem Thevenin. Prosedur Langkah demi Langkah. Pulih dari: Elektrikimologi.org
- Teorem Thevenin. Diselesaikan contoh langkah demi langkah. Diperolehi daripada: ElecticalSimple.Blogspot.com
- Bengkel mengenai teorem Thevenin dan Norton. Diperolehi dari: web.IIT.Edu
- Wikipedia. Teorem Thévenin. Pulih dari: wikipedia.com