Teorem Binomial

Apakah teorem binomial?

Dia Teorem Binomial Ini adalah persamaan yang memberitahu kita bagaimana ungkapan bentuk berkembang (a+b)ⁿ Untuk beberapa bilangan semula jadi n. Binomial tidak lebih daripada jumlah dua elemen, seperti (a+b). Ia juga membolehkan kita mengetahui istilah yang diberikan oleh^kb^N-K Apakah pekali yang mengiringi.

Teorem ini biasanya dikaitkan dengan pencipta bahasa Inggeris, ahli fizikal dan matematik Sir Isaac Newton; Walau bagaimanapun, pelbagai rekod telah dijumpai yang menunjukkan bahawa kewujudannya sudah diketahui di Timur Tengah, sekitar tahun 1000.

Nombor gabungan

Teorem binomial secara matematik memberitahu kita perkara berikut:

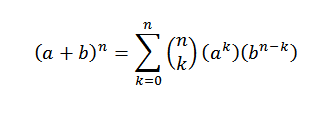
Dalam ungkapan ini A dan B adalah nombor sebenar dan n adalah nombor semula jadi.

Sebelum memberikan demonstrasi, mari kita lihat beberapa konsep asas yang diperlukan.

Nombor gabungan atau kombinasi N dalam k dinyatakan seperti berikut:

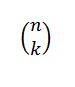
Ini menyatakan nilai berapa banyak subset dengan elemen k boleh dipilih dari satu set elemen N. Ekspresi algebra beliau diberikan oleh:

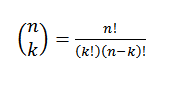
Mari kita lihat contoh: Katakan kita mempunyai sekumpulan tujuh bola, yang mana dua merah dan selebihnya berwarna biru.

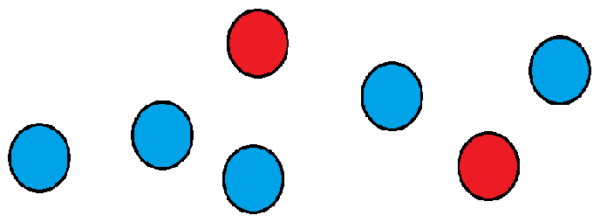
Kami ingin mengetahui berapa banyak cara yang dapat kami perintahkan mereka berturut -turut. Salah satu cara adalah untuk meletakkan dua merah di kedudukan pertama dan kedua, dan seluruh bola dalam kedudukan yang kekal.

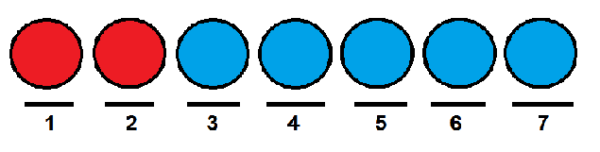
Sama dengan kes sebelumnya, kita dapat memberikan bola merah masing -masing kedudukan pertama dan terakhir, dan menduduki yang lain dengan bola biru.

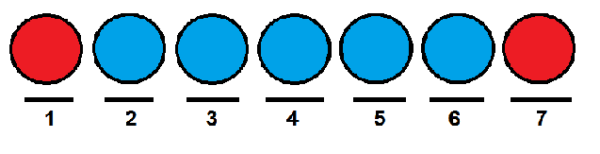
Sekarang, cara yang berkesan untuk mengira berapa banyak cara kita dapat memesan bola berturut -turut menggunakan nombor kombinatorial. Kita dapat melihat setiap kedudukan sebagai elemen set berikut:

Boleh melayani anda: nombor sempurna: bagaimana mengenal pasti dan contohnya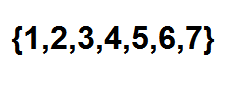

Di bawah hanya untuk memilih subset dua elemen, di mana setiap elemen ini mewakili kedudukan yang akan ditempati bola merah. Kita boleh melakukan pilihan ini mengikut hubungan yang diberikan oleh:

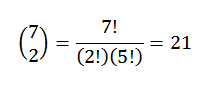
Dengan cara ini, kami mempunyai 21 cara untuk memerintahkan bola tersebut.

Idea umum contoh ini akan sangat berguna dalam demonstrasi teorem binomial. Mari kita lihat kes tertentu: jika n = 4, kita ada (a+b)⁴, Itu tidak lebih daripada:

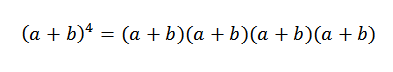
Apabila kita membangunkan produk ini, kita mempunyai jumlah terma yang diperoleh dengan mengalikan elemen setiap empat faktor (a+b). Oleh itu, kita akan mempunyai istilah yang akan dalam bentuk:

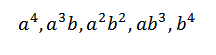
Sekiranya kita mahu mendapatkan istilah borang untuk⁴, Ia hanya cukup untuk membiak seperti berikut:

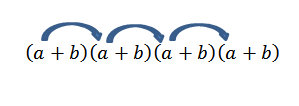
Perhatikan bahawa hanya ada satu cara untuk mendapatkan elemen ini; Tetapi apa yang berlaku jika kita sekarang mencari akhir borang²b²? Sebagai "A" dan "B" adalah nombor sebenar dan, oleh itu, ia bernilai undang -undang komutatif, kita perlu mendapatkan istilah ini adalah untuk membiak dengan ahli -ahli seperti yang ditunjukkan oleh anak panah.

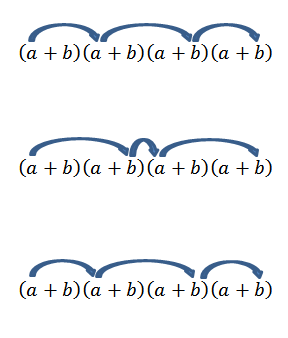
Melaksanakan semua operasi ini biasanya agak membosankan, tetapi jika kita melihat istilah "a" sebagai gabungan di mana kita ingin mengetahui berapa banyak cara kita boleh memilih dua "a" dari satu set empat faktor, kita boleh menggunakan idea tentang Contoh sebelumnya dari contoh sebelumnya. Jadi, kita mempunyai perkara berikut:

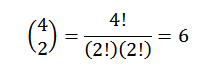
Oleh itu, kita tahu bahawa dalam perkembangan akhir ungkapan (a+b)⁴ Kami akan mempunyai tepat ke -6²b². Menggunakan idea yang sama untuk elemen lain, anda mesti:

Boleh melayani anda: nombor transenden: apakah, formula, contoh, latihan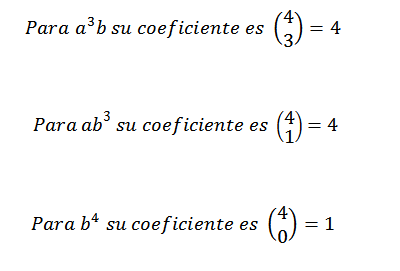

Kemudian kami menambah ungkapan yang diperolehi di atas dan kami perlu:

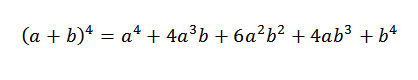
Ini adalah demonstrasi rasmi untuk kes umum di mana "n" adalah nombor semula jadi.

Demonstrasi

Perhatikan bahawa istilah yang tersisa semasa berkembang (a+b)ⁿ Mereka dari bentuk ke^kb^N-K, di mana k = 0.1, ..., n. Menggunakan idea contoh sebelumnya, kami mempunyai cara untuk memilih "K" pembolehubah "a" dari faktor "n" adalah:

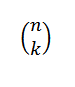
Apabila memilih dengan cara ini, kami secara automatik memilih pembolehubah N-K "B". Ini berikut:

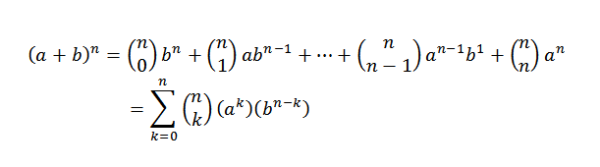
Contoh

Mempertimbangkan (a+b)⁵, Apa yang akan menjadi perkembangan anda?

Untuk teorem binomial kita perlu:

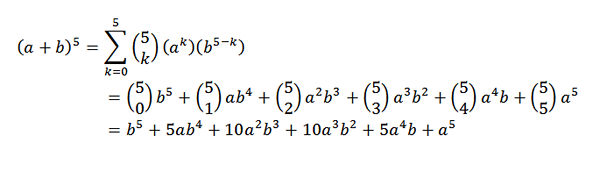
Teorem Binomial sangat berguna jika kita mempunyai ungkapan di mana kita ingin tahu apakah pekali istilah tertentu tanpa perlu melaksanakan pembangunan lengkap. Sebagai contoh, kita boleh mengambil perkara berikut yang tidak diketahui: Apakah pekali x⁷dan⁹ Dalam pembangunan (x + y)¹⁶?

Untuk teorem binomial, kita mempunyai pekali adalah:

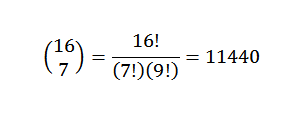
Contoh lain ialah: apakah pekali x⁵dan⁸ Dalam pembangunan (3x-7y)¹³?

Mula -mula kita menulis semula ungkapan dengan cara yang mudah; ini adalah:

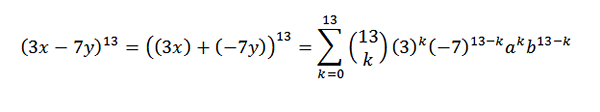
Kemudian, menggunakan teorem binomial, kami mempunyai pekali yang dicari adalah apabila anda mempunyai k = 5

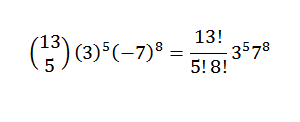
Satu lagi contoh penggunaan teorem ini adalah dalam demonstrasi beberapa identiti biasa, seperti yang akan kita sebutkan di bawah.

Identiti 1

Jika "n" adalah nombor semula jadi, kita perlu:

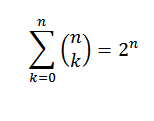
Untuk demonstrasi kami menggunakan teorem binomial, di mana kedua -duanya "a" dan "b" mengambil nilai 1. Maka kita ada:

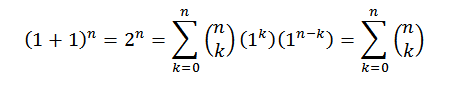
Dengan cara ini kita telah membuktikan identiti pertama.

Boleh melayani anda: pilihan rawak dengan atau tanpa penggantian

Identiti 2

Jika "n" adalah nombor semula jadi, maka

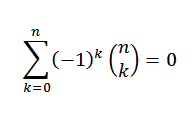
Untuk teorem binomial kita perlu:

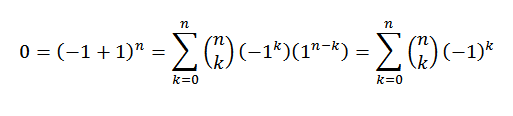
Demonstrasi lain

Kita boleh membuat demonstrasi yang berbeza untuk teorem binomial menggunakan kaedah induktif dan identiti Pascal, yang memberitahu kita bahawa, jika "n" dan "k" adalah bilangan bulat positif yang memenuhi n ≥ k, maka:

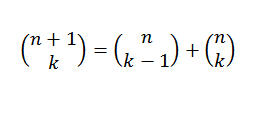
Demonstrasi induksi

Mari kita lihat bahawa asas induktif dipenuhi.  Jika n = 1, kita perlu:

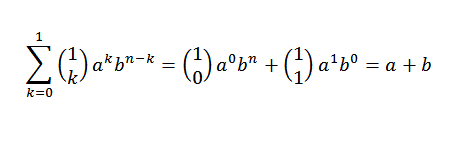
Memang, kita melihat bahawa ia dipenuhi. Sekarang, sama ada n = j sehingga ia dipenuhi:

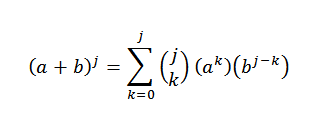
Kami mahu melihatnya untuk n = j+1 memang benar bahawa:

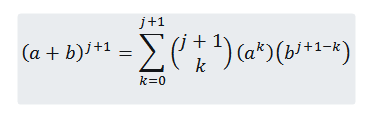
Jadi kita mesti:

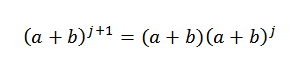
Dengan hipotesis kita tahu bahawa:

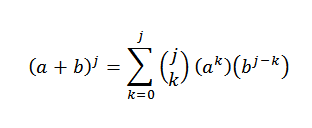
Kemudian, menggunakan harta pengedaran:

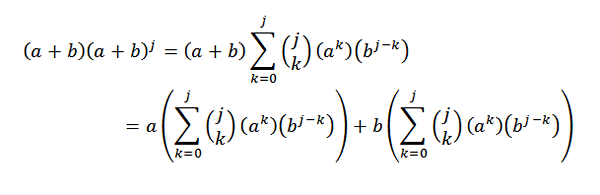
Seterusnya, membangunkan setiap ringkasan adalah:

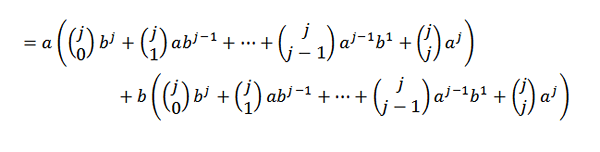
Sekarang, jika kita berkumpul dengan mudah, kita perlu:

Menggunakan identiti Pascal, kita mesti:

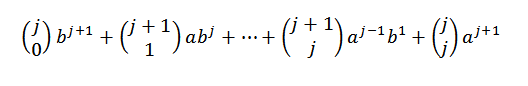
Akhirnya, perhatikan bahawa:

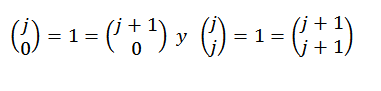
Oleh itu, kita melihat bahawa teorem binomial dipenuhi untuk setiap "n" milik nombor semula jadi, dan dengan ini ujian berakhir.

Curiosities

Nombor gabungan (NK) juga dipanggil pekali binomial kerana ia adalah tepat pekali yang muncul dalam pembangunan binomial (A+B)ⁿ.

Isaac Newton memberikan generalisasi teorem ini untuk kes di mana eksponen adalah nombor sebenar; Teorem ini dikenali sebagai Teorem Binomial Newton.

Sudah di zaman purba ini hasilnya dikenali untuk kes tertentu di mana n = 2. Kes ini disebutkan dalam Item daripada Euclid.