Tetradecágono

Apa itu tetradecágono?

Tetradecágono adalah angka geometri yang rata dan tertutup sebanyak 14 sisi, milik keluarga poligon. Ia juga dikenali dengan nama Tetrakaidecágono, Semua perkataan yang berasal dari kata -kata Yunani: "Tetra" (cuatri), "kai" (lebih banyak), "pereputan" (sepuluh) dan "gon" (sudut), kerana ia juga mempunyai 14 sudut dalaman.

Angka ini menunjukkan tetradagon biasa, iaitu, yang sisi dan sudut dalaman semuanya mempunyai ukuran yang sama, menunjukkan ciri -ciri utama angka ini.

Rajah 1.- Tetrade biasa dengan ciri -ciri utamanya. Sumber: f. Zapata.

Elemen Tetradecágono

• Sisi: Mereka dipanggil segmen 14 baris yang ditutup untuk membentuk angka tersebut. Mereka semua boleh mempunyai panjang yang sama, di mana poligon adalah biasa, atau mereka boleh berbeza dan kemudian ada tetrade yang tidak teratur.
• Simpang: Mereka adalah titik persimpangan antara segmen berturut -turut dan tetradecágono mempunyai 14 titik.
• Pusat: Titik yang sama dari simpul.
• Radio: segmen yang menyatukan pusat dengan puncak.
• Sudut dalaman: Ia dibentuk oleh bahagian dalam angka dan antara dua segmen berturut -turut atau bersebelahan. Langkah -langkah 154.286º untuk tetradecágon biasa, tanpa mengira saiz sisi.
• Sudut luaran: dibentuk di antara satu sisi dan pemanjangan salah satu sisi bersebelahan. Tidak kira panjang sampingan, sudut ini berukuran 25.7143º untuk tetrade biasa.
• Sudut pusat: Orang yang mempunyai puncaknya bertepatan dengan pusat poligon dan sisinya adalah dua radio berturut -turut.
• Pepenjuru: Segmen yang menghubungkan dua simpang yang tidak berkonsepkan.

Bagaimana tetradecágono?

Poligon biasa N sisi yang dibina dengan peraturan dan kompas mempunyai n dari Borang 2^r p₁... p_k, menjadi p_Yo Nombor Fermat Primo berbeza, dan seterusnya nombor Perdana Fermat mengambil bentuk 2ⁿ + 1.

Boleh melayani anda: Menunggu garis: formula dan persamaan, perwakilan, contoh

Tetradecágono mempunyai n = 14 sisi, tetapi 14 = 7 × 2, yang bukan sepupu fermat, kerana mereka tidak dapat dinyatakan dengan cara yang ditunjukkan. Oleh itu poligon ini tidak mengakui pembinaan yang tepat dengan peraturan dan kompas, tetapi pembinaan yang mendekati dengan baik, melalui beberapa kaedah.

Kaedah umum untuk membina poligon biasa

Berikut adalah kaedah umum (bukan satu -satunya) untuk membina poligon biasa yang didaftarkan dalam lilitan, termasuk tetrade biasa.

Ia terdiri daripada membahagikan diameter menegak lilitan ini ke dalam bahagian yang sama seperti sisi mempunyai poligon untuk menarik. Dalam kes tetradecágono mereka akan menjadi 14 bahagian bernombor dalam imej 2. Ini adalah langkah -langkah:

• Lukis diameter menegak dari A hingga B.
• Kemudian lukis separuh berat bermula dari titik A, buka kompas dengan pembukaan sewenang -wenangnya dan buat 14 bahagian yang sama jaraknya. Semirrect dan bahagiannya dapat keluar dari lilitan.
• Sertailah jenama 14va (berwarna biru dalam imej) pada akhir separuh dengan titik b.
• Untuk terus menyertai selebihnya tanda -tanda dalam separuh -rekreasi dengan titik masing -masing pada diameter menegak (titik hijau).
• Dengan hujung kompas dalam a dan pembukaan sama dengan ukuran diameter lilitan arka ditarik. Dengan ukuran yang sama, tetapi menyokong hujung dalam b (titik 14 dari Rajah 2) gerbang lain ditarik, yang dipotong dengan yang pertama di titik v dan v 'ditunjukkan.

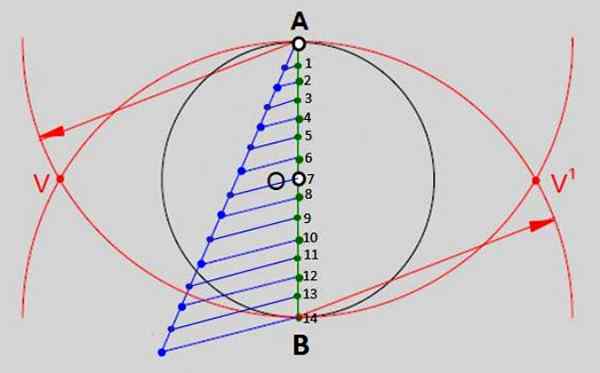Rajah 2.- Salah satu kaedah umum untuk membina poligon biasa adalah untuk membahagikan diameter lilitan ke seberapa banyak bahagian yang sama seperti sisi mempunyai poligon. Dalam kes tetradech biasa, terdapat 14 bahagian yang sama. Sumber: f. Zapata.

• Sekarang, dengan peraturan, lukis garis dari V 'ke titik 2 dan memanjangkannya untuk merentasi lilitan pada titik c Rajah 3. Tandakan titik persimpangan, yang akan menjadi salah satu simpang angka.

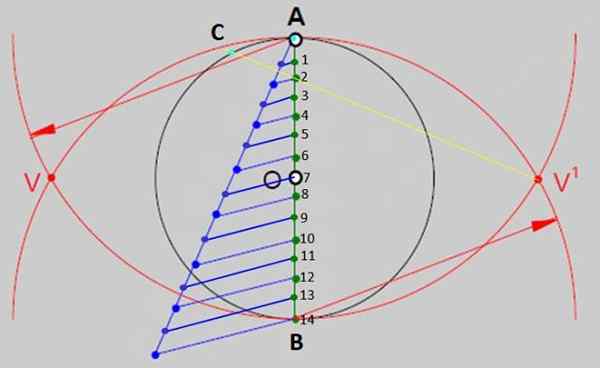Boleh melayani anda: cawangan statistik Rajah 3.- Segmen AC adalah ukuran sisi tetradecion yang dibina. Sumber: f. Zapata.

• Buka kompas di jarak AC dan menyokong hujung di A atau C, melukis gerbang ukuran yang sama ke seluruh lilitan, dengan cara ini dibahagikan kepada bahagian yang sama, persimpangan antara lengkungan dan lilitan adalah simpang adalah Vertices of Tetradecágono.
• Dengan peraturan, sertai simpang dengan segmen garis, membentuk sisi poligon.
• Padam dengan teliti pembinaan tambahan.

Dalam animasi berikut, satu lagi kaedah anggaran ditunjukkan, dengan peraturan dan kompas:

Rajah 4.- Animasi yang menunjukkan bagaimana tetradecágon dibuat (kira -kira poligon biasa). Sumber: Wikimedia Commons.

Formula untuk tetrade biasa

Formula berikut sah untuk poligon biasa:

• Nombor lembaran: n
• Ukuran sampingan: a
• Apothem: l_Ke
• Radio: r
• Perimeter: p
• Kawasan: a
• Sudut Dalaman: i
• Sudut luaran: e
• Diagonal: d

Bahagian yang diketahui ke apothem

A = 2L_Ke × tg (π/n)

Untuk n = 14:

A = 2L_Ke × TG (π/14)

Bahagian radio yang diketahui

A = 2R × Sen (π/n)

Ya n = 14:

A = 2R × Sen (π/14)

Perimeter yang dikenali di sebelah

Perimeter adalah jumlah sisi. Apabila tetradecágono biasa:

P = n op = 14 ⋅ a

Sekiranya tetradecágono tidak teratur, semua pihak mesti ditambah terus untuk mendapatkan perimeter.

Kawasan yang dikenali di sebelah

A = ¼ na² × katil (π/n)

Untuk n = 14:

A = ¼ (14hb²) × cot (π/14) = (7/2) a² × katil (π/14)

Kawasan yang diketahui

A = n ⋅L_Ke ² × tg (π/n)

Mengambil N = 14 Hasil:

A = 14L_Ke ² × TG (π/14)

Kawasan berdasarkan perimeter dan apothem

A = (p × l_Ke)/2

Boleh melayani anda: Teorem Bayes

Ukuran sudut dalaman

 Apabila n = 14, sudut dalaman tetradecágono mengukur darjah:

I = 12 × 180º /14 = 154.286º

Pengukuran sudut luaran

E = 360º/n

Apabila n = 14 anda mempunyai:

E = 25.7143º

Diagonal

Formula untuk mengira bilangan pepenjuru yang terdapat di mana -mana poligon, biasa atau tidak, adalah:

Untuk n = 14:

D = 14 × 11/2 = 77 Diagonal

Contoh

Satu lagi contoh tetradecágon

Poligon biasa muncul berulang kali dalam pelbagai reka bentuk, seperti mata wang. Dalam kes tetradagon biasa, ini muncul dalam duit syiling peringatan Malaysia, yang mewakili sisinya kepada setiap empat belas negara Konfederasi bangsa itu.

Concave dan cembung tetradecágonos

Secara umum, poligon seperti tetradecágono boleh cembung atau cekung, dalam kes pertama, ukuran sudut dalaman mereka tidak melebihi 180º. Tetradech biasa adalah cembung, seperti mana -mana poligon biasa, kerana mana -mana sudut dalamannya berukuran 154.286º.

Sebaliknya, di tetradech cekung, satu atau lebih sudut dalamannya berukuran lebih daripada 180º.

Contoh berangka

Memandangkan tetradagon biasa yang sebelahnya mengukur 5 cm, cari:

a) perimeter
b) Pengukuran apothem
c) Panjang radio
d) kawasan

Jawapan

a) Kerana ia adalah poligon biasa, perimeter adalah:

P = 14 × 5 cm = 70 cm.

b) dari persamaan a = 2l_Ke × tg (π/14), di mana a = 5 cm, apothem l_Ke:

L_Ke = A / [2 × Tg (π / 14)] = 5 cm / 0.4565 = 21.9064 cm

c) Radio R boleh dikira oleh a = 2r × sen (π/14):

R = a / [2 × sin (π / 14)] = 5 cm / 0.4565 = 22.4698 cm

d) Terdapat beberapa alternatif untuk kawasan tersebut, contohnya a = (p × l_Ke)/2:

A = (70 × 21.9064)/2 cm² = 1533.45 cm².

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Arturo Geometry. Kaedah umum untuk melukis poligon yang didaftarkan di lilitan. Pulih dari YouTube.com
3. Kalkulator sup. Kalkulator Poligon Biasa. Pulih dari: calculatoroup.com.
4. Lukisan. Poligon biasa. Pulih dari: melukis.com.
5. Requena, b. Poligon Concave. Pulih dari: universoformulas.com.
6. Wikipedia. Poligon yang boleh dibina. Pulih dari: Adakah.Wikipedia.org.