Jenis fungsi dan graf mereka

Terdapat pelbagai Jenis fungsi yang digunakan untuk memodelkan masalah dalam cabang pengetahuan seperti sains semula jadi, pentadbiran, ekonomi dan sains sosial. Secara matematik, fungsi adalah hubungan antara dua atau lebih pembolehubah.

Banyak kali, objek atau kuantiti tertentu berkaitan antara satu sama lain. Jumlah ini diwakili oleh pembolehubah. Sebagai contoh, terdapat dua pembolehubah yang berkaitan, yang dimiliki oleh dua set A dan B, tidak semestinya berangka, walaupun kebanyakan masa mereka-.

Untuk dianggap sebagai fungsi, hubungan ini mesti memenuhi dua syarat: yang pertama adalah bahawa semua unsur -unsur set permulaan untuk mengambil bahagian, dan yang kedua, bahawa setiap elemen set tersebut berkaitan dengan hanya satu unsur set b.

Pembolehubah biasanya dipanggil dengan huruf x dan dan, dengan x sebagai pembolehubah bebas dan dan sebagai pemboleh ubah bergantung. Sememangnya, mereka boleh dipanggil dengan cara lain, memilih nama pembolehubah mengikut magnitud yang diwakilinya.

Hubungan antara keduanya dilambangkan melalui surat itu F -atau satu lagi huruf abjad-, dan diwakili dalam beberapa cara, seperti satu set pasangan yang diperintahkan, graf, ungkapan lisan atau formula algebra:

• f (x) = x + 1
• Penduduk p dari bandar tertentu dalam selang waktu tertentu t.
• H (x) = (1,3); (2,4); (3,5); (4.6)

Fungsi dicirikan dengan mempunyai domain dan julat atau laluan. Domain adalah set nilai yang pembolehubah x Anda boleh mengambil, sementara julat adalah set nilai yang memperoleh fungsi bergantung atau pembolehubah dan.

Klasifikasi fungsi

Fungsi ini boleh dikumpulkan ke dalam 5 kategori besar, seperti yang ditunjukkan dalam skim berikut, di mana setiap kumpulan dilabelkan dengan nombor Rom dan warna. Bermula dari kiri ke kanan, fungsi diklasifikasikan mengikut:

• I) Bentuknya.
• Ii) simetri.
• Iii) Cara untuk menyatakan pembolehubah.
• Iv) kesinambungan dan monotoninya.
• V) Cara di mana unsur -unsur domain berkaitan dengan julat.

Kriteria klasifikasi utama untuk fungsi. Sumber: f. Zapata.

Sekarang ikuti penerangan ringkas setiap jenis fungsi dengan contoh masing -masing.

I) fungsi mengikut bentuknya

Yo.1) Fungsi algebra

Mereka adalah antara fungsi yang paling banyak digunakan dalam pelbagai bidang sains, dan oleh itu mereka adalah yang paling terkenal. Mereka dicirikan dengan mempunyai peraturan surat -menyurat, ungkapan algebra.

Sebaliknya, fungsi algebra dibahagikan kepada jenis berikut:

• Yo.1.a) polinomial atau polinomial.
• Yo.1.b) rasional.
• Yo.1.c) tidak rasional.
• Yo.1.d) mengikut bahagian.

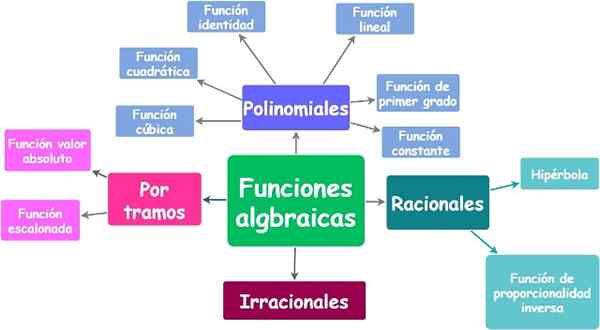Fungsi algebra dan jenis mereka. Sumber: f. Zapata.

Yo.1.a) fungsi polinomial atau polinomial

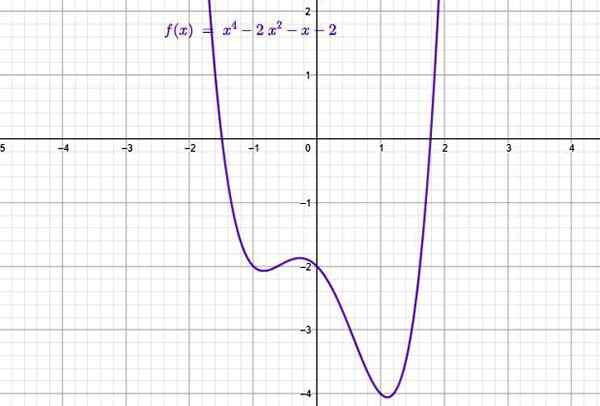Contoh fungsi jenis polinomial. Sumber: f. Zapata melalui geogebra.

Mereka terdiri daripada jumlah istilah yang bentuk umumnya:

P (x) = a_nxⁿ + ke _N-1x^N-1 +... ke₁x + a₀

Di mana koefisien ke_n, ke _N-1... ke₁, ke₀ Mereka nombor sebenar dan n adalah integer. Domain fungsi polinomial adalah set r nombor sebenar dan juga fungsi berterusan di seluruh domain tersebut.

Dalam angka atas adalah graf fungsi polinomial berikut Pesanan 4:

f (x) = x⁴ - 2x² - x -2

Di antara fungsi polinomial, beberapa kes tertentu dibezakan, mengikut nilai pekali. Perlu dipertimbangkan dengan teliti, kerana mereka sangat berguna dalam pelbagai situasi:

i) fungsi berterusan

Terdapat fungsi yang berterusan apabila semua pekali dibatalkan, kecuali₀:

f (x) = a₀ = k

Grafik fungsi malar adalah garis lurus selari dengan paksi mendatar, seperti garis:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

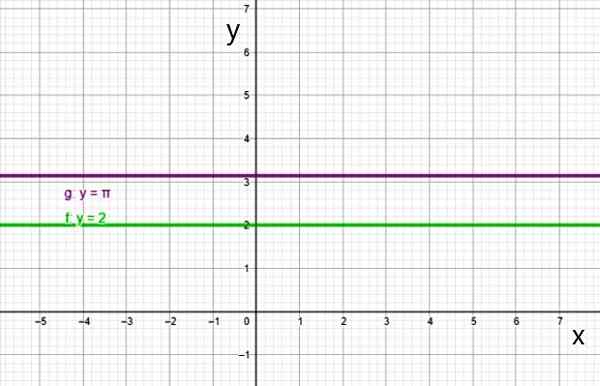Dua contoh fungsi malar. Sumber: f. Zapata.

Ii) Fungsi ijazah pertama

Fungsi pertama atau fungsi yang berkaitan ialah grafnya adalah garis lurus. Ia adalah kes tertentu fungsi polinomial di mana semua pekali pembatalan₁ sudah₀. Ia diberikan oleh:

f (x) = a₁x + a₀

Nilai a₁ Ia adalah cerun garis, yang memberikan ukuran kecenderungannya, dan₀ Ia adalah potongan garis dengan paksi menegak. Kedua -duanya boleh mengambil nilai positif atau negatif.

Contoh fungsi ijazah pertama adalah seperti berikut:

• G (x) = 2x -1
• H (x) = -6x +5/2

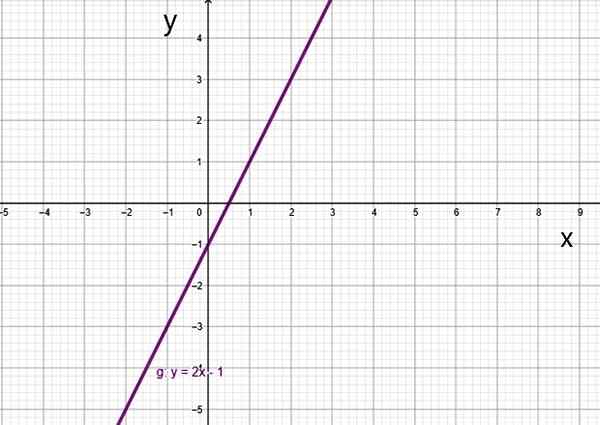Fungsi darjah pertama f (x) = 2x-1. Sumber: f. Zapata.

Terdapat kes khas, iaitu fungsi linear.

Boleh melayani anda: Langkah -langkah kecenderungan pusat untuk data dikumpulkan: formula, latihan

iii) fungsi linear

Apabila pekali untuk₀ Ia adalah 0, fungsi selalu melalui asal dan dinyatakan oleh f (x) = a₁X, memanggil funtion lineal, apa khabar:

• f (x) = 5x
• G (x) = -7x

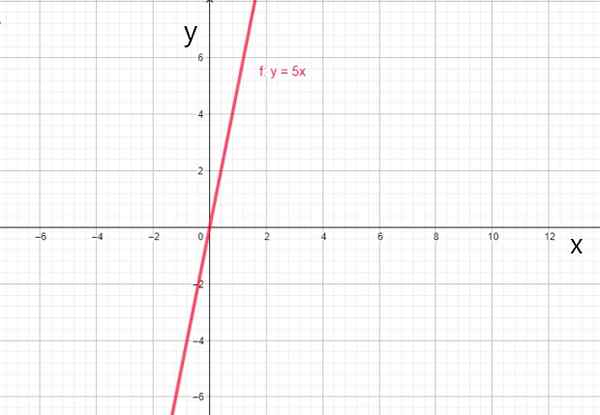Fungsi linear f (x) = 5x. Sumber: f. Zapata.

iv) fungsi identiti

Ia adalah kes tertentu fungsi linear, di mana₁ = 1:

f (x) = x

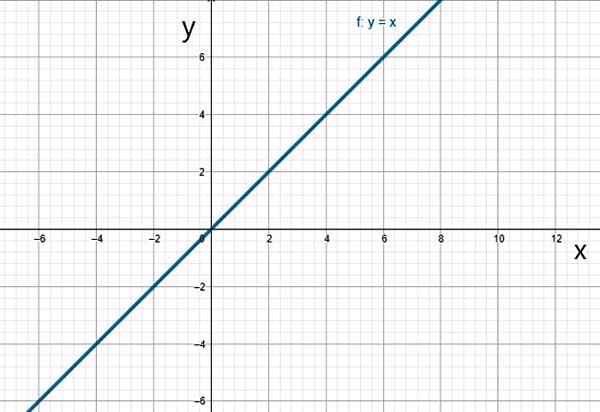Fungsi identiti. Sumber: f. Zapata.

v) fungsi kuadratik

Ia mempunyai bentuk umum:

f (x) = a₂x² +ke₁x + a₀

Dengan₂  ≠ 0.

Grafnya adalah perumpamaan yang paksi paksi atau simetri selari dengan paksi ordinat. Selalu memotong paksi menegak pada titik koordinat x = 0, y = a₀. Bagi persimpangan dengan paksi mendatar, ia boleh mempunyai maksimum 2.

Contoh fungsi kuadrat adalah:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

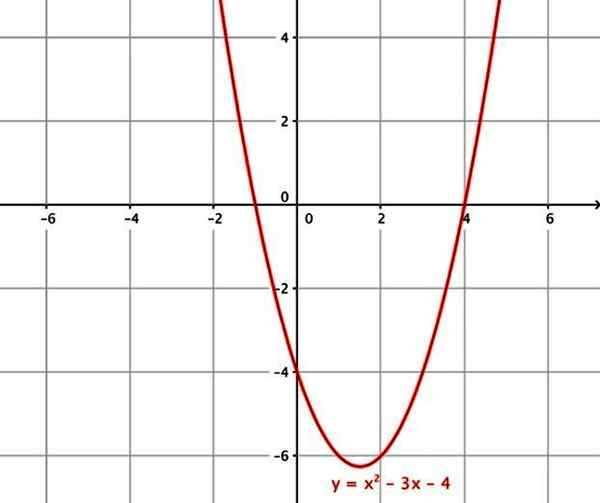Fungsi kuadratik. Sumber: Wikimedia Commons.

vi) fungsi padu

Seperti namanya, fungsi padu mengandungi kuasa 3:

f (x) = a₃x³ + ke₂x² + ke₁x + a₀

Pekali a₃ Ia sentiasa berbeza dari 0, seperti dalam kes ini:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

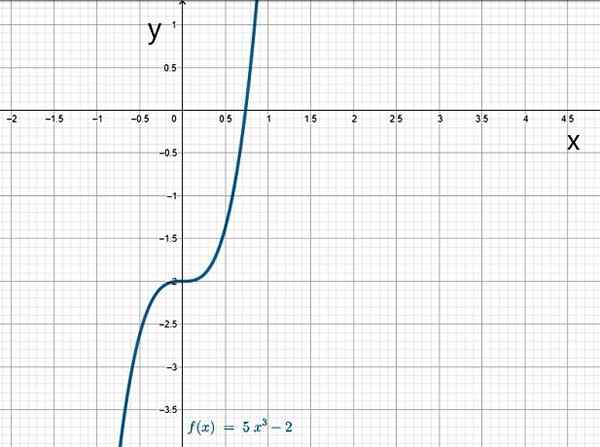Fungsi padu. Sumber: f. Zapata.

Yo.1.b) fungsi rasional

Fungsi rasional mempunyai bentuk:

 Di mana p (x) dan q (x) adalah polinomial yang tidak dapat dielakkan, iaitu, mereka tidak mempunyai faktor yang sama dan dalam mana -mana kes q (x) ≠ 0.

Dari domain fungsi rasional, semua nilai yang membatalkan penyebut q (x), iaitu akarnya, sementara nilai -nilai nilai -nilai nilai dan yang menentukan asymptot mendatar.

Asymptote adalah garis yang berfungsi, baik di sebelah kiri dan di sebelah kanan, di atas atau di bawah, tetapi tidak pernah melintasi. Garis sedemikian boleh menegak, mendatar atau cenderung.

Contoh fungsi rasional adalah:

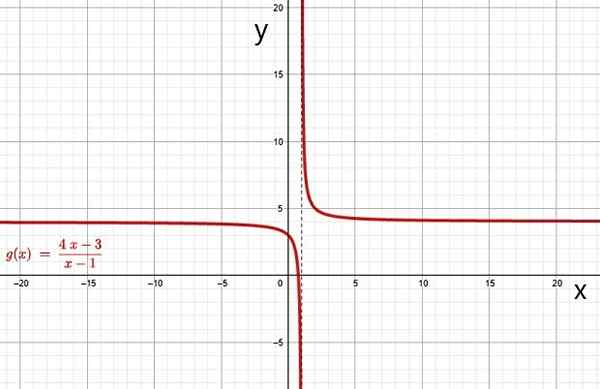Fungsi rasional. Sumber: f. Zapata melalui geogebra.

i) Hyperbola

Grafik fungsi rasional adalah hiperbola apabila polinomial dalam penyebut q (x) mempunyai gred 1. Grafik fungsi f (x) dan g (x) contoh -contoh di atas adalah hiperbola, ia dapat dengan mudah diperiksa melalui perisian grafik dalam talian percuma, seperti geogebra.

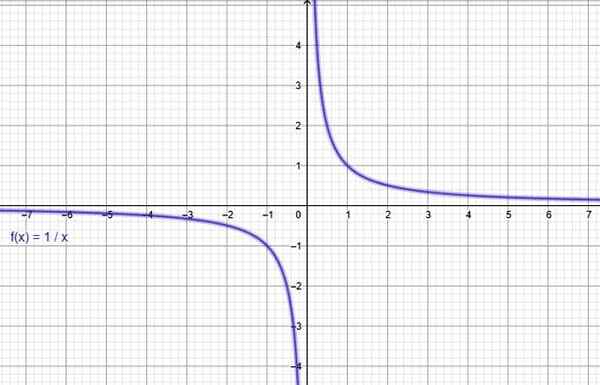Fungsi y = 1/x. Sumber: f. Zapata melalui geogebra.

Ii) Fungsi perkadaran songsang

Ia adalah fungsi bentuk:

Di mana c adalah nombor sebenar yang berbeza dari 0. Domainnya adalah set nombor sebenar kecuali 0.

Yo.1.c) fungsi tidak rasional

Adalah mereka yang pembolehubah bebas berada di bawah tanda radikal. Bentuk umumnya ialah:

Beberapa fungsi ini boleh:

• 
• 

Domain fungsi ini ditentukan seperti berikut:

-Sekiranya akarnya indeks tork, jumlah subradikal f (x) mesti selalu 0 atau positif.

-Apabila akarnya ganjil, f (x) boleh positif atau negatif. Oleh itu dalam kes ini, domain fungsi adalah nombor sebenar.

Sebagai contoh, domain:

Ia adalah set nombor nyata sehingga x-3 lebih besar daripada atau sama dengan 0. Dalam kes ini, x mestilah lebih besar daripada atau sama dengan 3. Oleh itu, domain fungsi ini adalah set nilai selang [3, ∞+).

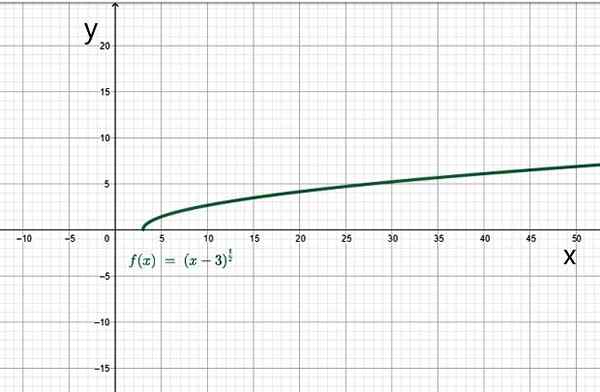 Contoh fungsi yang tidak rasional. Sumber: f. Zapata.

Yo.1.d) fungsi ke kepingan atau bahagian

Fungsi di bahagian, mengikut bahagian atau kepingan adalah yang memerlukan lebih daripada satu formula untuk nilai domain yang berbeza. Berikut adalah beberapa contoh permohonan anda:

-Kadar untuk menghantar pakej melalui pos, bergantung pada berat atau isipadu, asal dan destinasi yang sama.

-Kadar untuk perkhidmatan, contohnya telefoni dan elektrik.

-Penjualan tiket untuk muzium atau taman hiburan, bergantung pada usia.

Dalam bentuk matematik, fungsi dalam bahagian boleh, sebagai contoh:

Domain fungsi di bahagian bergantung pada definisi. Dalam contoh sebelumnya, domain adalah set yang dibentuk oleh: (-∞, -1) ∪ [1,+∞).

Fungsi nilai mutlak. Sumber: f. Zapata melalui geogebra.

Ii) fungsi eskalonada

Grafik fungsi ini oleh bahagian terdiri daripada langkah -langkah, seperti tangga atau boleh menjadi ketinggian yang berbeza, bergantung pada cara fungsi ditakrifkan.

Ia boleh melayani anda: Hipparco of Nicea: Biografi dan Sumbangan kepada Sains

Untuk ini, selang terhingga [a, b] dipilih yang mengandungi bilangan ketahanan tertentu tertentu, yang dipanggil x_Yo < x₁ < x₂ <… . x_n  Dan selang terbuka dipilih (x_Yo , x_i+1) Untuk memberikan nilai s tetap_Yo, Dengan lompatan pada titik x_Yo. Nilai s_Yo Ia adalah ketinggian langkah yang dipersoalkan.

Contoh fungsi berperingkat adalah seluruh bahagian, yang mengambil nombor dan mengaitkannya dengan integer berikut, sama ada dengan berlebihan atau secara lalai. Berikut adalah bahagian keseluruhan:

[x] = (integer yang lebih besar ≤ x)

Menurut fungsi ini, seluruh bahagian 2.5 adalah:

[2.5] = (integer yang lebih besar ≤ 2.5) = 2

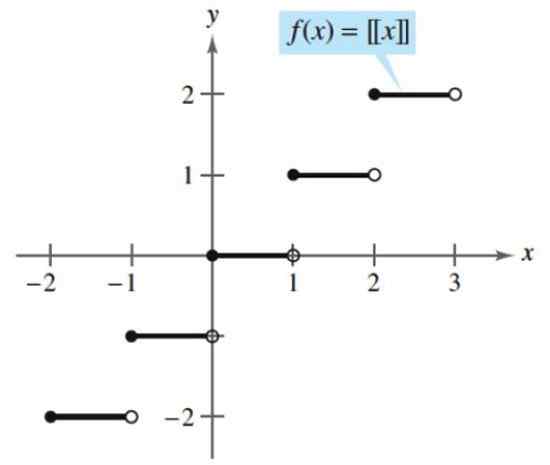Seluruh bahagian. Sumber: Larson, r. Pengiraan dengan geometri analisis. McGraw-Hill.

Yo.2) fungsi transenden

Fungsi bukan algebra dipanggil transenden. Fungsi eksponen, logaritma dan trigonometri adalah fungsi transenden.

Di dalamnya pemboleh ubah x Ia adalah sebahagian daripada hujah fungsi atau sebagai sebahagian daripada eksponen atau indeks beberapa akar, sebagai contoh:

• f (x) = log (x+1)
• H (x) = -0.28^-3x

Fungsi transenden mempunyai banyak aplikasi, contohnya dalam kajian getaran dan gelombang, pengagihan kebarangkalian, pemodelan gelombang, pertumbuhan populasi yang pelbagai, kerosakan radioaktif, kadar faedah dan banyak lagi. 

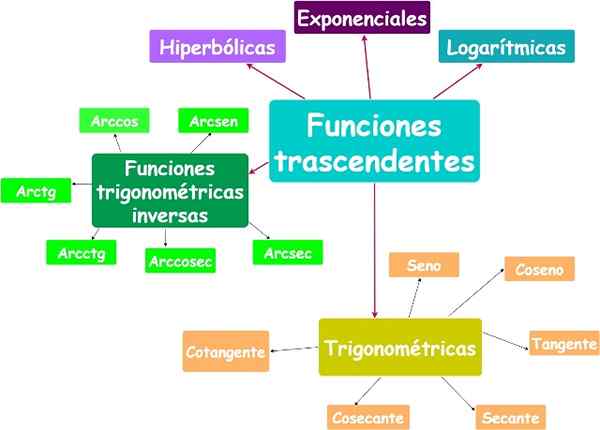Fungsi transenden utama. Sumber: f. Zapata.

Yo.2.a) fungsi eksponen 

Fungsi eksponen ditakrifkan oleh:

f (x) = a^x

Di mana A adalah asas, yang selalu merupakan bilangan positif 1, dan pemboleh ubah, nombor sebenar, muncul di eksponen. Secara umum, fungsi eksponen ditulis:

F (x) = a^Bx

Di sini A dan B adalah pekali sebenar. Berikut adalah fungsi jenis ini:

• f (x) = 5e^x
• H (x) = 4. 10^5x
• g (t) = 8e^-2t

Asas dan, di mana dan Ia adalah jumlah euler 2.71828 ..., sering muncul dalam masalah sains dan kejuruteraan, serta statistik. Apabila fungsi mempunyai asas ini dipanggil Fungsi eksponen semulajadi.

Domain fungsi eksponen adalah set nombor sebenar, sementara julatnya adalah nombor positif.

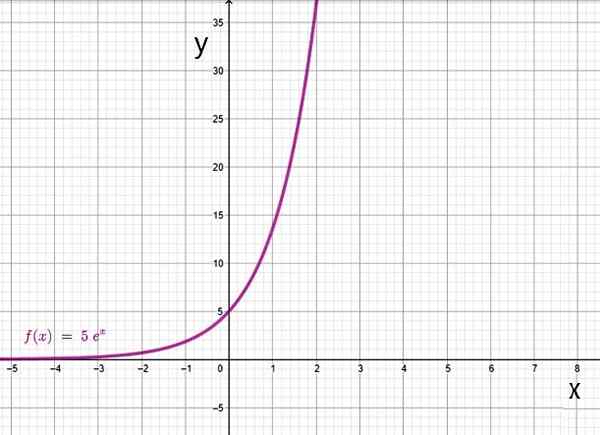Fungsi eksponen berdasarkan. Sumber: f. Zapata melalui geogebra.

Yo.2.b) fungsi logaritma

Bagi bahagiannya, fungsi logaritma berdasarkan ke Ia adalah fungsi songsang fungsi eksponen berdasarkan ke. Yeah:

log_ke x = y

Jadi:

x = a^dan

Khususnya, jika asas logaritma adalah nombor E, fungsi dipanggil Fungsi logaritma Neperian Dan ia dilambangkan sebagai Ln. Fungsi jenis ini adalah:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - log x²

Domain fungsi logaritma, tanpa mengira asas, adalah nombor sebenar positif, tidak termasuk 0. Iaitu, tidak ada logaritma nombor negatif atau 0.

Walau bagaimanapun, logaritma boleh menjadi 0 atau negatif: logaritma nombor antara 0 dan 1 adalah negatif dan bagi bahagiannya mencapai_ke 1 = 0.

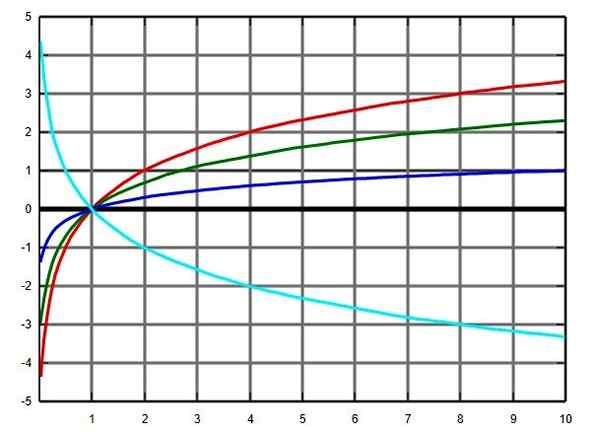Grafik fungsi logaritma di beberapa pangkalan: asas 2 dalam merah, hijau e, biru -base dan turquoise di pangkalan 0.5. Sumber: Wikimedia Commons.

Yo.2.c) fungsi trigonometri

Mereka adalah mereka yang berasal dari sebab -sebab trigonometri: sinus, kosinus, tangen, pengeringan, harmoni dan cotangen sudut x. Mereka dilambangkan masing -masing sebagai:

Sen x, cos x, tg x, sec x, bahaya x dan cotg x

Mereka adalah fungsi berkala, yang bermaksud bahawa bentuknya berulang -ulang, jadi mereka sangat berguna untuk menggambarkan fenomena semulajadi seperti isyarat, ayunan, pergerakan pekeliling dan pergerakan swing, yang dicirikan dengan berulang -ulang.

Contoh fungsi trigonometri adalah:

• f (x) = sin x
• G (t) = 5 ⋅ cos (ωt + π)
• H (x) = Tg (x/2)

Variabel x dinyatakan dalam radian.

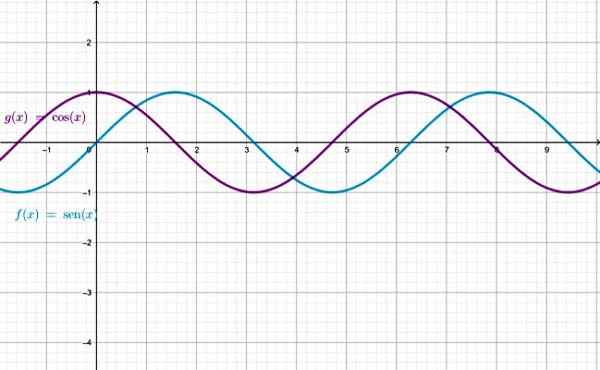Graf fungsi sen x dan cos x, ambil perhatian bahawa mereka sama, kecuali yang dipindahkan berkenaan dengan yang lain. Sumber: f. Zapata melalui geogebra.

Penguasaan fungsi Sen X dan COS X, adalah set nombor sebenar. Untuk fungsi selebihnya terdapat nilai x yang mana fungsi tidak ditakrifkan:

-Fungsi Tg x tidak wujud apabila x = ± π /2, ± 5π /2 ... Ini adalah, semua gandaan ganjil π /2.

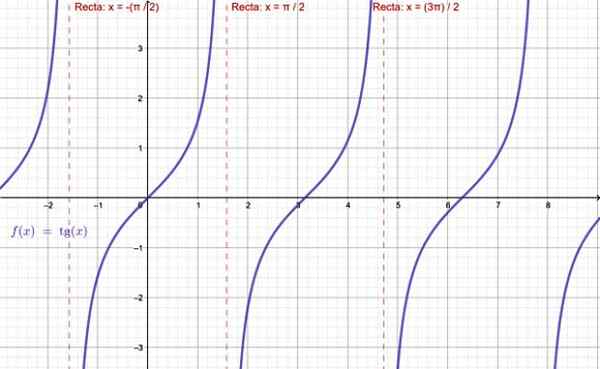Grafik fungsi tangen. Sumber: f. Zapata melalui geogebra.

-Bagi f (x) = cotg x, fungsi ini tidak ditakrifkan untuk keseluruhan gandaan π: ± π, ± 2π, ± 3π ..

Boleh melayani anda: Undang -undang tanda

-Fungsi y = sec x tidak sah apabila cos x = 0, yang tidak termasuk x = ± π /2, ± 5π /2 ... domainnya.

-Akhirnya, untuk f (x) = bahaya x, seluruh gandaan π tidak tergolong dalam domain mereka.

Yo.2.d) fungsi hiperbola

Fungsi hiperbolik adalah kombinasi khas eksponen dan^x dan e^-x Dan mereka dipanggil sebagai pangkuan, Coseno .. .hiperbolik. Seperti fungsi trigonometri, juga dipanggil "bulat", terdapat 6 fungsi hiperbola:

-Sinus hiperbolik SenH X:

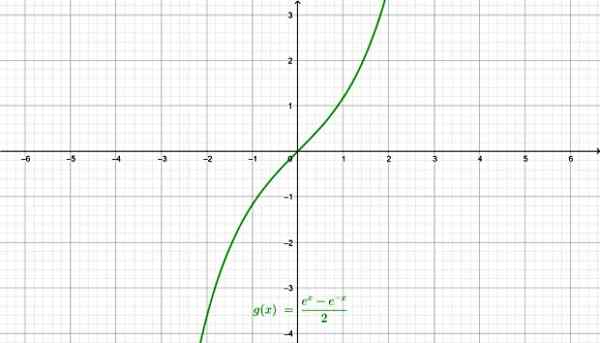Fungsi sinus hiperbolik. Sumber: f. Zapata melalui geogebra.

-Cosine hiperbolik COSH X:

 -Tangen hiperbolik Tanh x:

 -Harvester Hyperbolic CSCH X:

 -Hyperbolic Secant Sech x:

-Cotangent hiperbolik Coth x:

Kabel fleksibel, diperbuat daripada bahan seragam dan gantung antara dua titik, mengambil bentuk lengkung yang dipanggil Catenary, yang dinyatakan sebagai kosinus hiperbolik:

Yo.2.e) fungsi trigonometri songsang

Mereka sesuai dengan kebalikan fungsi trigonometri. Sebagai contoh, apa yang akan menjadi sudut (arka) yang pangkuannya bernilai 0.5?

Jawapannya adalah arc sen 0.5, yang berbunyi "arka sinus 0.5 ", dan sudut ini adalah 30º, walaupun pada dasarnya, ini tidak akan menjadi satu -satunya sudut yang pangkuannya bernilai 0.5, kerana fungsi Sen x berkala. Apa yang berlaku ialah jika fungsi Sen x diambil di seluruh domainnya, ia tidak akan terbalik, jadi fungsi Arcoseno tidak dapat ditakrifkan. Isu ini diselesaikan dengan menyekat segala -galanya ke sudut antara -π/2 dan +π/2.

Ini boleh dinyatakan seperti berikut:

Sekiranya arka sen x = θ, ini bermaksud bahawa dosa θ = x

Dengan -π/2 ≤ θ ≤ π/2.

Notasi lain yang digunakan untuk arka sen x adalah f (x) = dosa^-1 x. Grafik ditunjukkan di bawah:

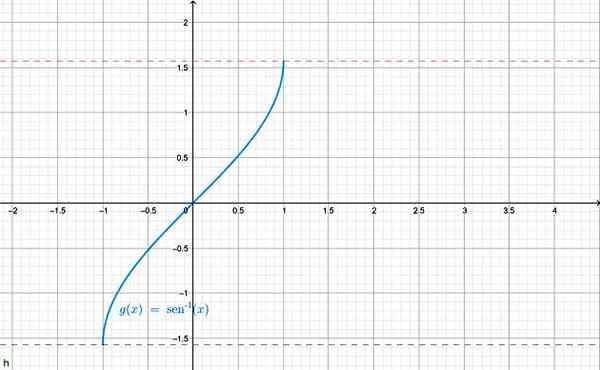Grafik fungsi arcsen x. Sumber: f. Zapata melalui geogebra.

Ia juga mungkin untuk menentukan songsang untuk fungsi trigonometri yang lain, contohnya: arka cos x = θ dan oleh itu. Bagi setiap pangkatnya dibatasi dengan betul, menjadi kebalikan dari fungsi trigonometri yang sepadan.

Ii) Fungsi mengikut simetrinya

Ii.1) par

Jika untuk semua x milik domain f (x) ia dipenuhi bahawa:

f (x) = f (-x)

Dikatakan bahawa fungsi itu juga, seperti yang berikut:

• f (x) = x² - 3
• g (x) = cos x
• 

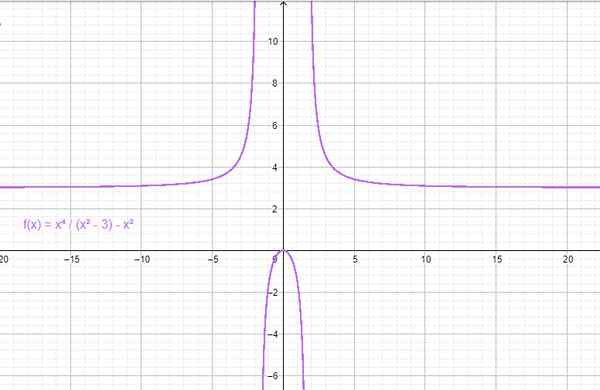  Contoh fungsi pasangan. Sumber: f. Zapata melalui geogebra.

Contohnya, melakukan x = 1 inci f (x) = x² - 3 diperoleh:

F (1) = 1² - 3 = -2.

Dan jika x = -1, maka:

f (-1) = (-1)² - 3 = -2.

Kedua -dua keputusan adalah sama.

Fungsi juga mempunyai simetri di sekitar paksi menegak, seperti yang dapat dilihat pada angka sebelumnya.

Ii.2) Fungsi ganjil

Sebaliknya, ya:

f (-x) = -f (x)

Fungsi ini ganjil.

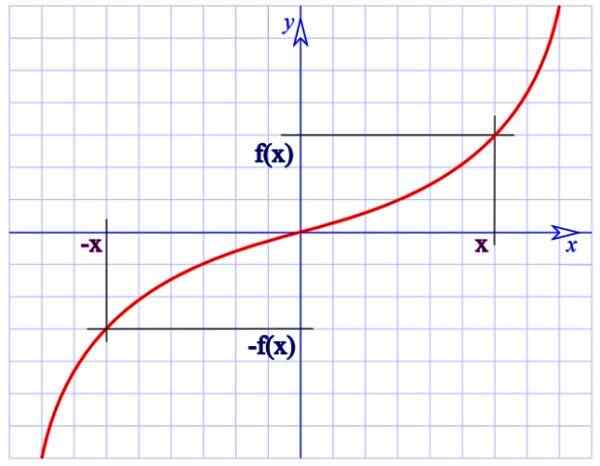Fungsi ganjil. Sumber: Wikimedia Commons.

Contohnya fungsi f (x) = 1/x angka atas adalah ganjil, kerana:

f (-x) = -1/x

Dan

-f (x) = -1/x

Satu lagi fungsi impar penting ialah f (x) = sin x.

Perhatikan bahawa fungsi ganjil mempunyai simetri putaran 180º di sekitar asal (graf tidak diubah jika setiap titiknya bertukar 180º berkenaan dengan asal koordinat).

Iii) berfungsi mengikut ungkapan pembolehubah

Iii.1) Fungsi eksplisit

Mereka dinyatakan secara langsung dari segi pemboleh ubah bergantung seperti y = f (x). Sebagai contoh:

• f (x) = x³

Iii.2) fungsi tersirat

Dalam fungsi tersirat, tiada pembolehubah kelihatan jelas. Mereka dinyatakan sebagai f (x, y) = 0, seperti:

• x² + dan² -3xy = 0
• xy = - x²+ X-5

Fungsi yang diterangkan sepanjang artikel ini adalah fungsi yang jelas.

Iv) Fungsi mengikut grafik anda

Menurut graf mereka, fungsi -fungsi itu boleh berterusan atau tidak berterusan. Fungsi berterusan dapat dikesan tanpa mengganggu strok, sebaliknya, fungsi tidak berterusan lompat. Dalam imej berikut, fungsi tidak berterusan pada x = a:

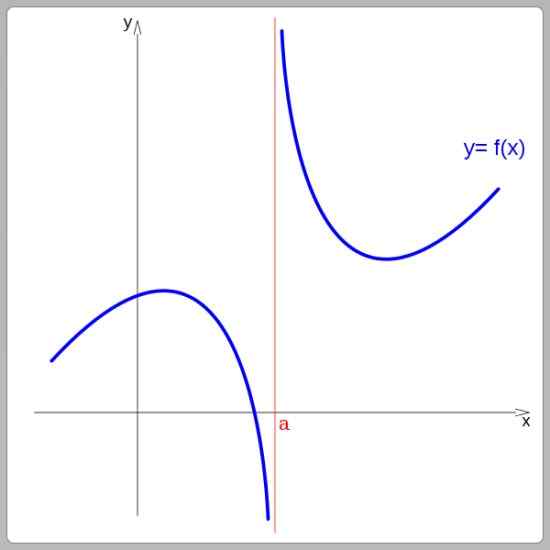Fungsi pemotongan pada x = a. Sumber: Wikimedia Commons.

Contoh fungsi berterusan adalah fungsi linear, fungsi kuadratik dan fungsi sinus dan kosinus. Dan antara fungsi yang tidak berterusan adalah fungsi yang berperingkat dan fungsi tangen.

V) Fungsi mengikut hubungan antara unsur -unsur domain dan julat

V.1) fungsi injektif

Fungsi adalah Injective Apabila tidak ada dua elemen yang berbeza dalam set permulaan atau domain, yang mempunyai imej yang sama dalam set ketibaan.

Katakan bahawa fungsi sebenar mempunyai, melainkan dinyatakan sebaliknya, sebagai contoh:

f (x) = 5x -2

Semua nilai x milik domain f (x), yang merupakan set ℛ nombor sebenar, mempunyai imej yang unik, juga sebenar. Sebaliknya, dalam fungsi lain ini:

g (x) = x²

Terdapat unsur yang berbeza dalam domain yang mempunyai imej yang sama, contohnya x₁= 2 dan x₂= -2:

G (2) = g (-2) = 4.

Cara untuk mengenal pasti fungsi injektif dari grafnya adalah melukis garis mendatar, jika ia dipotong ke lengkung pada lebih dari satu titik, fungsi itu bukan imbasan.

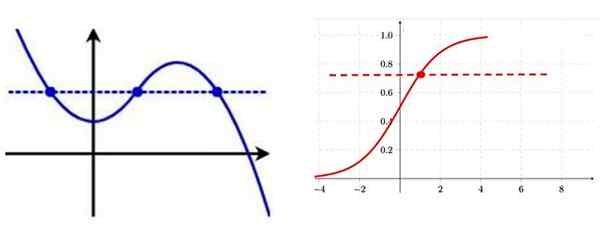Di sebelah kiri fungsi Injak PBB, ambil perhatian bahawa terdapat beberapa titik graf dengan koordinat menegak yang sama. Di sebelah kanan fungsi injektif, di setiap titik lengkungnya ia mempunyai koordinat "y" tertentu. Sumber: f. Zapata.

V.2) fungsi overjektif

Di dalam fungsi onjective, Semua elemen set ketibaan adalah imej beberapa elemen set permulaan. Contoh fungsi overjective adalah sama f (x) = 5x -2, tetapi g (x) = x² Tidak, kerana nilai -nilai yang diambil g (x) hanya yang positif dan 0.

Walau bagaimanapun, domain itu boleh ditakrifkan semula supaya g (x) terlalu banyak, jika contohnya ia berubah kepada semua yang positif yang positif ditambah 0. 

V.3) Fungsi bijective

Akhir Bijektif. Contoh fungsi bi ini adalah: fungsi yang berkaitan, fungsi eksponen dan fungsi logaritma.

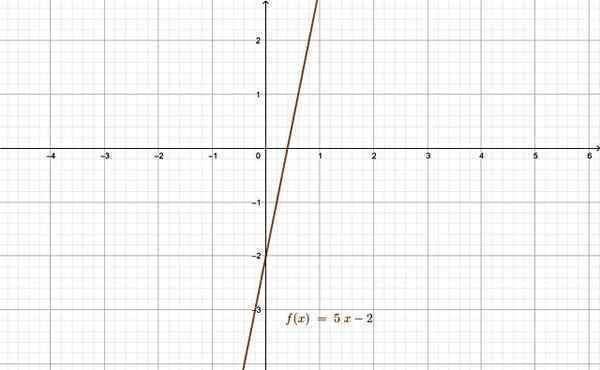Fungsi yang berkaitan adalah contoh fungsi Bijjective yang baik. Sumber: f. Zapata melalui geogebra.

Rujukan

1. Zon e-math. Jenis fungsi. Pulih dari: emathzone.com.
2. Hoffman, J.G. Pemilihan masalah matematik. Ed. Spphinx.
3. Matematik menyeronokkan. Rujukan fungsi Commons. Pulih dari: Mathisfun.com.
4. Requena, b. Formula Universe. Jenis fungsi. Pulih dari: universoformulas.com.
5. Stewart, J. 2006. Preccculment: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.