Ciri -ciri pukulan parabola, formula dan persamaan, contoh

Dia pukulan parabola Ia terdiri daripada membuang objek atau peluru dengan sudut tertentu dan membiarkannya bergerak di bawah tindakan graviti. Jika rintangan udara tidak dipertimbangkan, objek, tanpa mengira sifatnya, akan mengikuti trajektori dalam bentuk parabola.

Ia adalah pergerakan harian, kerana di antara sukan yang paling popular adalah di mana bola atau bola dilemparkan, sama ada dengan tangan, dengan kaki atau dengan instrumen seperti raket atau kelawar misalnya.

Rajah 1. Jet air dari sumber hiasan mengikuti trajektori parabola. Sumber: Wikimedia Commons. Zátonyi Sandor (IFJ.), Fizped/cc by-sa (https: // creativeCommons.Org/lesen/by-sa/3.0)

Untuk kajian, pukulan parabola dipecahkan kepada dua pergerakan bertindih: satu mendatar tanpa pecutan, dan menegak yang lain dengan pecutan berterusan ke bawah, iaitu graviti. Kedua -dua pergerakan mempunyai kelajuan awal.

Katakan pergerakan mendatar memerlukan. Setiap pergerakan ini bebas daripada yang lain.

Memandangkan hakikat bahawa menentukan kedudukan peluru adalah objektif utama, perlu memilih sistem rujukan yang sesuai. Perinciannya datang seterusnya.

[TOC]

Formula dan persamaan pukulan parabola

Katakan objek dilemparkan dengan sudut α berkenaan dengan kelajuan mendatar dan awal v_{Sama ada} seperti yang ditunjukkan dalam angka di bawah ke kiri. Pukulan parabola adalah pergerakan yang berlaku di atas kapal terbang Xy Dan dalam hal ini kelajuan awal terurai seperti ini:

v_lembu = v_{Sama ada} cos α

v_Oy = v_{Sama ada} dosa α

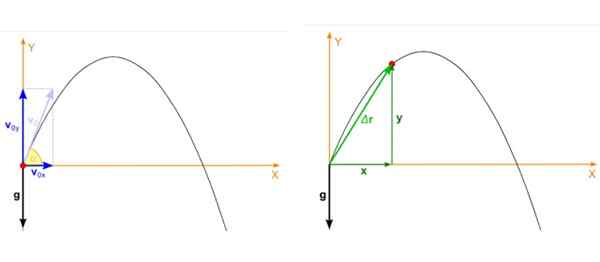Rajah 2. Di sebelah kiri kelajuan awal peluru dan ke kanan kedudukan pada bila -bila masa pelancaran. Sumber: Wikimedia Commons. Zátonyi Sandor, (IFJ.) Fizped/cc by-sa (https: // creativeCommons.Org/lesen/by-sa/3.0).

Kedudukan peluru, yang merupakan titik merah dalam Rajah 2, imej kanan, juga mempunyai dua komponen yang bergantung pada masa, satu di x Dan yang lain di dan. Kedudukannya adalah vektor yang dilambangkan sebagai r dan unitnya panjang.

Dapat melayani anda: isomeria

Dalam angka itu, kedudukan awal peluru bertepatan dengan asal sistem koordinat, oleh itu x_{Sama ada} = 0, dan_{Sama ada} = 0. Ini tidak selalu berlaku, asalnya boleh dipilih di mana sahaja, tetapi pilihan ini memudahkan pengiraan.

Bagi kedua -dua pergerakan dalam x dan y, ini adalah:

-X (t): ia adalah pergerakan rectilinear seragam.

-dan (t): sepadan dengan pergerakan rectilinear yang dipercepatkan secara seragam dengan g = 9.8 m/s² dan menunjuk secara menegak ke bawah.

Dalam bentuk matematik:

x (t) = v_{Sama ada} cos α.t

dan (t) = v_{Sama ada} .dosa α.T - ½g.t²

Vektor kedudukan kekal:

r (t) = [v_{Sama ada} cos α.t]Yo + [v_{Sama ada} .dosa α.T - ½g.t²] J

Dalam persamaan ini pembaca yang penuh perhatian akan melihat bahawa tanda tolak adalah disebabkan oleh fakta bahawa keparahan menunjuk ke tanah, rasa yang dipilih sebagai negatif, sementara ke atas ia diambil sebagai positif.

Oleh kerana kelajuan adalah yang pertama diperoleh dari kedudukan, sudah cukup untuk memperoleh r (t) Mengenai masa dan mendapatkan:

v (t) = v_{Sama ada} cos α Yo + (v_{Sama ada} .dosa α - Gt) J

Akhirnya pecutan dinyatakan secara vektor sebagai:

ke (t) = -g J

- Trajektori, ketinggian maksimum, masa maksimum dan jangkauan mendatar

Trajektori

Untuk mencari persamaan eksplisit trajektori, iaitu lengkung y (x), anda perlu menghapuskan parameter masa, penjelasan dalam persamaan untuk x (t) dan menggantikan y (t). Penyederhanaan agak susah payah, tetapi akhirnya diperoleh:

Ketinggian maksimum

Ketinggian maksimum berlaku ketika v_dan = 0. Mengetahui bahawa terdapat hubungan seterusnya antara kedudukan dan kuadrat kelajuan:

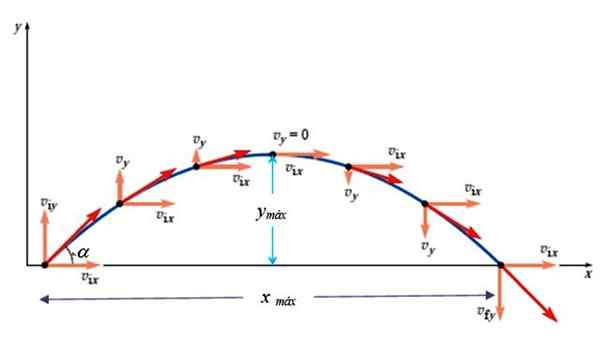Rajah 3. Kelajuan dalam pukulan parabola. Sumber: Giambattista, a. Fizik.

v_dan² = v_Oy ²- 2Gy

Melakukan v_dan = 0 Hanya apabila mencapai ketinggian maksimum:

0 = v_Oy ²- 2 g.dan_maks → dan_maks = v_Oy ²/2 g

Dengan:

Boleh melayani anda: pecutan centripetal: definisi, formula, pengiraan, latihan

v_Oy = v_{Sama ada} senα

Masa maksimum

Masa maksimum adalah masa objek yang diperlukan untuk dicapai dan_maks. Untuk mengira ia digunakan:

v_dan = v_{Sama ada} .dosa α - Gt

Mengetahui bahawa v_dan Ia dilakukan 0 ketika t = t_maks, Hasilnya:

v_{Sama ada} .dosa α - g.t_maks = 0

t_maks = v_Oy /g

Julat mendatar maksimum dan masa penerbangan

Skop sangat penting, kerana ia menunjukkan di mana objek akan jatuh. Oleh itu, kita akan tahu sama ada ia memberikan putih atau tidak. Untuk menemukannya, kita memerlukan masa penerbangan, jumlah masa atau t_v.

Dari ilustrasi sebelumnya, mudah untuk menyimpulkan bahawa t_v = 2.t_maks. Tetapi perhatian hanya benar jika pelancaran berada pada tahap, iaitu, ketinggian titik permulaan adalah sama dengan ketinggian ketibaan. Jika tidak, masa menyelesaikan persamaan darjah kedua yang disebabkan oleh menggantikan kedudukan akhir dan_final:

dan_final = v_{Sama ada} .dosa α.t_v - ½g.t_v²

Walau apa pun, skop mendatar maksimum ialah:

x_maks = v_lembu. t_v

Contoh menembak parabola

Pukulan parabola adalah sebahagian daripada pergerakan orang dan haiwan. Juga hampir semua sukan dan permainan di mana graviti campur tangan. Sebagai contoh:

Menembak parabola dalam aktiviti manusia

-Batu yang dilemparkan oleh berliku -liku.

-Tendangan gol penjaga gawang.

-Bola yang melemparkan periuk.

-Anak panah yang keluar dari gerbang.

-Semua jenis lompat

-Membuang batu.

-Mana -mana senjata membuang.

Rajah 4. Batu yang dibuang oleh Catapult dan Ball Patey di kotak penamat adalah contoh tembakan parabola. Sumber: Wikimedia Commons.

Parabolik ditembak dalam alam semula jadi

-Air tumbuh dari jet semula jadi atau buatan seperti sumber.

-Batu dan lava tumbuh dari gunung berapi.

-Bola yang melantun di atas trotoar atau batu yang melakukannya di atas air.

-Semua jenis haiwan yang melompat: kangaroos, lumba -lumba, gazelles, felines, katak, arnab atau serangga, untuk menyebut beberapa.

Ia boleh melayani anda: kuasa mekanikal: apakah, aplikasi, contohRajah 5. Impala dapat melompat sehingga 3 m. Sumber: Wikimedia Commons. Arturo de Frias Marques/CC BY-S (https: // creativeCommons.Org/lesen/by-sa/3.0).

Senaman

Belalang membentuk sudut 55 º dengan mendatar dan tanah pada 0.80 meter kemudian. Cari:

a) Ketinggian maksimum dicapai.

b) Sekiranya saya melompat dengan kelajuan awal yang sama, tetapi membentuk sudut 45º, adakah ia akan menjadi lebih tinggi?

c) Apa yang boleh dikatakan mengenai jangkauan mendatar maksimum untuk sudut ini?

Penyelesaian kepada

Apabila data yang disediakan oleh masalah tidak mengandungi halaju awal v_{Sama ada} Pengiraannya agak lebih susah payah, tetapi dari persamaan yang diketahui, ungkapan baru dapat disimpulkan. Bermula dari:

x_maks = v_lembu . t_penerbangan = v_{Sama ada}.cos α. t_v

Apabila ia mendarat kemudian, ketinggian adalah 0 lagi, kemudian:

v_{Sama ada} .dosa α.t_v - ½g.t_v²= 0

Sebagai t_v Ini adalah faktor biasa, ia dipermudahkan:

v_{Sama ada} .dosa α - ½g.t_v= 0

Kita boleh membersihkan t_v Dari persamaan pertama:

t_v = x_maks / v_{Sama ada}.cos α

Dan ganti di tempat kedua:

v_{Sama ada} .dosa α - (½g.x_maks / v_{Sama ada}.cos α) = 0

Dengan mengalikan semua istilah oleh v_{Sama ada}.cos αEkspresi tidak berubah dan penyebutnya hilang:

(v_{Sama ada} .dosa α.) (v_{Sama ada}.cos α) - ½g.x_maks = 0

v_{Sama ada}² dosa α. cos α = ½g.x_maks

Sudah dapat dibersihkan v_{Sama ada} atau juga ganti identiti berikut:

Sen 2α = 2 sen α. cos α → V_{Sama ada}² Sen 2α = g.x_maks

Dikira v_{Sama ada}²:

v_{Sama ada}² = g.x_maks / Sen 2α = (9.8 x 0.8 / sen 110) m²/s² = 8.34 m²/s²

Dan akhirnya ketinggian maksimum:

dan_maks= v_Oy ²/2g = (8.34 x Sen² 55)/(2 x 9.8) m = 0.286 m = 28.6 cm

Penyelesaian b

Lobster berjaya mengekalkan kelajuan mendatar yang sama, tetapi apabila sudut berkurangan:

dan_maks= v_Oy ²/2g = (8.34 x Sen² 45)/(2 x 9.8) m = 0.213 m = 21.3 cm

Mencapai ketinggian yang lebih kecil.

Penyelesaian c

Skop mendatar maksimum ialah:

x_maks = v_{Sama ada}² Sen 2a / g

Apabila sudut berbeza -beza, skop mendatar juga berubah:

x_maks = 8.3. 4 Sen 90 / 9.8  m = 0.851 m = 85.1 cm

Lompatan lebih lama sekarang. Pembaca boleh mengesahkan bahawa ia adalah maksimum untuk sudut 45 º kemudian:

sin 2α = sin 90 = 1.

Rujukan

1. Figueroa, d. 2005. Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB).
2. GiMbattista, a. 2010. Fizik. Edisi kedua. McGraw Hill.
3. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
4. Resnick, r. 1999. Fizikal. Vol. 1. Edisi ke -3. dalam bahasa Sepanyol. Syarikat Editorial Continental s.Ke. daripada c.V.
5. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.