Ciri -ciri pukulan parabola, formula, persamaan, contohnya

Dia Pukulan parabola sewajarnya Ia adalah kes tertentu pergerakan jatuh bebas di mana kelajuan awal peluru membentuk sudut tertentu dengan mendatar, mengakibatkan jalan parabola.

Kejatuhan bebas adalah kes pergerakan dengan pecutan berterusan, di mana pecutan adalah graviti, yang selalu menunjuk secara menegak dan mempunyai magnitud 9.8 m/s^2. Ia tidak bergantung pada doh peluru, seperti yang ditunjukkan oleh Galileo Galilei pada tahun 1604.

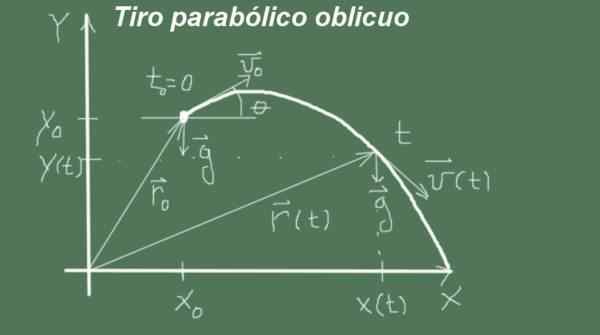
Rajah 1. Pukulan parabola sewajarnya. (Huraian sendiri)

Sekiranya kelajuan peluru awal menegak, kejatuhan bebas mempunyai trajektori lurus dan menegak, tetapi jika kelajuan awal maka serong trajektori kejatuhan bebas adalah lengkung parabola, juga ditunjukkan oleh Galileo.

Contoh pergerakan parabola adalah trajektori yang mengikuti besbol, peluru yang dipecat oleh meriam dan jet air yang keluar dari hos.

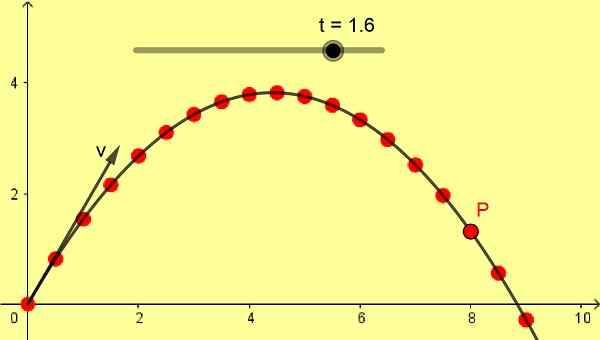
Rajah 1 menunjukkan pukulan parabola serong 10 m/s dengan sudut 60º. Skala dalam meter dan kedudukan P berturut -turut diambil dengan perbezaan 0.1 s bermula dari saat awal 0 saat.

[TOC]

Formula

Pergerakan zarah digambarkan sepenuhnya jika kedudukannya diketahui, kelajuannya dan pecutannya sebagai fungsi masa.

Pergerakan parabola yang terhasil daripada pukulan serong adalah superposisi pergerakan mendatar pada kelajuan tetap, ditambah dengan pergerakan menegak dengan pecutan tetap sama dengan pecutan graviti.

Formula yang digunakan untuk pukulan parabola serong adalah yang sesuai dengan pergerakan dengan pecutan berterusan a = g, Perhatikan bahawa berani telah digunakan untuk menunjukkan bahawa pecutan adalah jumlah vektor.

Boleh melayani anda: satelit semula jadi

Kedudukan dan kelajuan 

Dalam pergerakan pecutan yang berterusan, kedudukannya secara matematik bergantung pada masa dengan cara kuadrat.

Jika kita menunjukkan r(T) Kedudukan ke masa t, rSama ada Kedudukan segera awal, vSama ada Kelajuan awal, g pecutan dan t = 0 Sebagai momen awal formula yang memberikan kedudukan untuk setiap saat t adalah:

r(t) = r_{Sama ada} + v_{Sama ada} T + ½ g t²

Bold dalam ungkapan sebelumnya menunjukkan bahawa ia adalah persamaan vektor.

Kelajuan sebagai fungsi masa diperoleh daripada mengambil derivatif berkenaan dengan t kedudukan dan hasilnya adalah:

v(t) = v_{Sama ada} + g t

Dan untuk mendapatkan pecutan sebagai fungsi masa, kelajuan yang diperoleh dari t Hasil:

ke(t) = g

Apabila masa tidak tersedia, terdapat hubungan antara kelajuan dan kedudukan, yang diberikan oleh:

v² = vSama ada² - 2 g (dan - saya)

Persamaan

Seterusnya kita akan menemui persamaan yang digunakan untuk pukulan parabola serong dalam bentuk Cartesian.

Rajah 2. Pembolehubah dan parameter pukulan parabola serong. (Huraian sendiri)

Pergerakan bermula pada masa ini t = 0 Dengan kedudukan awal (Xo, saya) dan kelajuan magnitud vSama ada dan sudut θ, iaitu vektor halaju awal adalah (vSama ada cosθ, vSama ada senθ). Pergerakan berlalu dengan pecutan 

g = (0, -g).

Persamaan Parametrik

Sekiranya formula vektor yang memberikan kedudukan sebagai fungsi masa digunakan dan komponen dikumpulkan dan disamakan, persamaan yang diberikan oleh koordinat kedudukan ke mana -mana masa t akan diperolehi.

x (t) = x_{Sama ada} + v_lembu t 

dan (t) = y_{Sama ada} + v_Oy t -½ g t²

Begitu juga, persamaan mempunyai komponen kelajuan sebagai fungsi masa.

Ia boleh melayani anda: usaha biasa: Apa yang terdiri daripada, bagaimana ia dikira, contohnya

v_x(t) = v_lembu

v_dan(t) = v_Oy - g t 

Di mana: v_lembu = vSama ada cosθ; v_Oy = vSama ada Senθ

Persamaan trajektori

y = a x^2 + b x + c

A = -g/(2 vlembu^2)

B = (vOy/vlembu + g xSama ada/vlembu^2)

C = (danSama ada - vOy xSama ada / vlembu)

Contoh 

Contoh 1

Jawab soalan berikut:

a) Mengapa masalah menembak parabola biasanya menghina kesan geseran dengan udara?

b) Adakah bentuk objek dalam pukulan parabola?

Jawapan

a) Bagi pergerakan peluru menjadi parabola, adalah penting bahawa daya geseran udara jauh lebih rendah daripada berat objek yang dilancarkan. 

Sekiranya bola gabus atau bahan ringan dilemparkan, daya geseran dapat dibandingkan dengan berat badan dan trajektorinya tidak dapat mendekati parabola.

Sebaliknya, jika ia adalah objek berat seperti batu, daya geseran boleh diabaikan berbanding dengan berat batu dan trajektorinya hampir dengan parabola.

b) Bentuk objek yang dilancarkan juga relevan. Sekiranya Plata kapal terbang dalam bentuk avionncito dilancarkan, pergerakannya tidak akan bebas atau parabola, kerana bentuknya nikmat rintangan udara.

Sebaliknya, jika lembaran kertas yang sama padat dalam bentuk bola, pergerakan yang dihasilkan sangat mirip dengan parabola.

Contoh 2

Sebuah peluru dilancarkan dari lantai mendatar dengan cepat 10 m/s dan 60º sudut. Ini adalah data yang sama dengan Rajah 1 telah dibangunkan. Dengan data ini saya dapati:

a) momen di mana ia mencapai ketinggian maksimum.

Boleh melayani anda: apakah sifat terma dan apa itu? (Dengan contoh)

b) ketinggian maksimum.

c) kelajuan pada ketinggian maksimum.

d) Kedudukan dan kelajuan pada 1.6 s.

e) ketika dia memainkan tanah lagi.

f) Skop mendatar.

Penyelesaian untuk)

Kelajuan menegak bergantung pada masa adalah

v_dan(t) = v_Oy - G t = v_{Sama ada} Senθ - g t = 10 sen60º - 9.8 t = 8.66 - 9.8 t 

Pada masa ketinggian maksimum dicapai kelajuan menegak adalah sifar untuk seketika.   

8.66 - 9.8 t = 0 ⇒ t = 0.88 s.

Penyelesaian b)

Ketinggian maksimum diberikan oleh koordinat dan Buat masa ini di mana ketinggian itu dicapai:

dan (0.88s) = Yo saya akan t -½ g t^2 = 0 + 8.66*0.88-½ 9.8 0.88^2 = 

3.83 m

Oleh itu ketinggian maksimum ialah 3.83 m.

Penyelesaian c)

Kelajuan pada ketinggian maksimum adalah mendatar:

v_x(t) = v_lembu = v_{Sama ada} cosθ = 10 cos60º = 5 m/s 

D) penyelesaian

Kedudukan pada 1.6 s adalah:

X (1.6) = 5*1.6 = 8.0 m

dan (1.6) = 8.66*1.6-½ 9.8 1.62 = 1.31 m

Penyelesaian e)

Apabila koordinat menyentuh dan dibatalkan, maka:

dan (t) = 8.66*t -½ 9.8 t2 = 0 ⇒ t = 1.77 s

Penyelesaian f)

Skop mendatar adalah koordinat x tepat pada masa ini yang memainkan tanah:

X (1.77) = 5*1.77 = 8.85 m

Contoh 3

Cari persamaan trajektori dengan contoh 2 data.

Penyelesaian 

Persamaan parametrik trajektori adalah:

x (t) = 5*t

dan (t) = 8.66*t -½ 9.8 T^2

Dan persamaan Cartesian diperolehi dengan membersihkan t yang pertama dan diganti di tempat kedua

y = 8.66*(x/5) -½ 9.8 (x/5)^2

Memudahkan:

y = 1.73 x - 0.20 x^2 

Rujukan

1. P. P. Teodorescu (2007). "Kinematik". Sistem Mekanikal, Model Klasik: Mekanik Zarah. Springer.
2. Resnick, Halliday & Krane (2002). Fizik Volume 1. Cecsa, Mexico.
3. Thomas Wallace Wright (1896). Unsur -unsur mekanik termasuk kinematik, kinetik dan statik. E dan fn spon.
4. Wikipedia. Pergerakan parabola. Pulih dari ES.Wikipedia.org.
5. Wikipedia. Gerakan projektil.Diambil dari.Wikipedia.org.