Toroid atau Toro Dona

Kami menerangkan apa lembu atau lembu jantan, ciri -ciri, kelantangan, permukaan, aplikasi dan menunjukkan beberapa contoh

Apa itu Toroid?

Dia Toroid Ia adalah badan geometri tiga dimensi dalam bentuk gelung, cincin, cincin, donat atau donat, oleh itu nama "Toro Dona", yang dimiliki oleh kelas yang dipanggil objek yang dipanggil Revolusi pepejal.

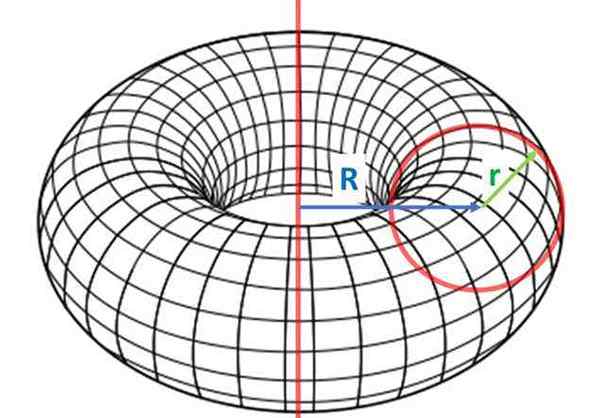
Toroid dihasilkan oleh berputar angka rata tertutup, sekitar garis milik satah yang sama angka, tetapi tidak memintasnya, seperti yang ditunjukkan di bawah:

Lembu, yang merupakan permukaan revolusi yang diperolehi dengan memutar angka rata tertutup (sebagai lilitan) di sekitar paksi tetap. Sumber: Wikimedia Commons

Ciri utama toroid ialah, walaupun permukaan tertutup, ia mempunyai lubang. Ini bermakna bahawa dua titik permukaannya dapat dihubungkan dengan segmen yang berada di luar objek.

Ciri lain dari toroid adalah bahawa ia adalah angka tiga dimensi tanpa simpul. Ciri ini berkongsi dengan badan -badan volumetrik lain seperti sfera, tetapi sementara sfera adalah permukaan cembung, lembu serentak serentak dan cembung.

Antara Bulls, lembu jantan Ia adalah yang paling biasa dan diperoleh dari putaran bulatan radio r, Mengenai paksi jarak jauh R yang pertama. Radio R (huruf kecil) dikenali sebagai jejari kecil dan r (modal) adalah jejari terbesar.

Kelantangan toroid

Lembu dijana dengan berputar di kawasan rata tertutup Ke sekitar paksi putaran yang tidak memotongnya. Menandakan oleh R Jarak dari paksi ke centroid angka rata, jumlah lembu revolusi adalah:

Boleh melayani anda: Fungsi trigonometri songsang: nilai, derivatif, contoh, latihan

V = 2πr ⋅ a 

Hasil ini diperoleh apabila memohon Teorem Pappus Untuk jumlah pepejal revolusi, yang menyatakan bahawa jumlah revolusi pepejal diperoleh dengan mengalikan kawasan angka yang dipecahkan oleh perimeter lilitan yang dibentuk oleh putaran centroid (atau pusat graviti ) dari angka berputar, di sekitar paksi putaran.

Kelantangan lembu jantan

Lembu adalah toroid yang dihasilkan oleh bulatan radio r. Jika jarak paksi putaran ke pusat bulatan diputar adalah r, maka perlu untuk kelantangan lembu itu:

V = (2πr) ⋅ (πr²) = 2π²R³

Permukaan lembu jantan

Jadilah angka rata yang hanya berkaitan Ke dan kontur L. Jika angka sedemikian diputar di sekitar paksi yang terkandung dalam satah yang sama angka, tetapi itu tidak menyeberanginya, maka permukaan yang dihasilkan adalah lembu jantan:

S = 2πr ⋅ l

Menjadi jarak dari paksi ke pusat graviti atau centroid, dari angka Generatrix.

Hasil ini adalah akibat dari Teorem Pappus Untuk permukaan pepejal revolusi.

Permukaan lembu jantan

Lembu Radio Radio Radio R (huruf kecil) dan Radio Radio R (huruf besar) adalah lembu tertentu yang dipanggil Toro.

Sebagai kontur l dari lingkaran radius r adalah 2πr, Kemudian kawasan permukaan lembu itu adalah:

S = (2πr) ⋅ (2πr) = (4π²) (R ⋅ r)

Aplikasi Toroid

Kerana ciri -ciri geometri, lembu itu mempunyai banyak aplikasi praktikal dan budaya. Untuk memulakan, gelung atau cincin adalah bahagian toroidal yang mempunyai pelbagai kegunaan:

Boleh melayani anda: dataran minimum

Budaya

• Penggunaan hiasan atau kosmetik apabila cincin diletakkan di atas jari, atau ketika menusuk diletakkan di telinga.
• Di hidung lembu, gelung diletakkan, yang berfungsi untuk mengikatnya dan mengawalnya.
• Apabila cincin atau cincin diletakkan di sebelah kiri pada jari cincin, maka ia mempunyai konotasi sosial, yang bermula dari masa orang Yunani kuno, dan menandakan komitmen, kesetiaan dan perkahwinan dengan pasangan yang membawa gelung yang sama cara dan bahan.

Dalam mekanik

Di luar konteks hiasan, kosmetik dan budaya, lembu jantan mempunyai banyak aplikasi praktikal. Dalam mekanik, toroid digunakan sebagai cincin pengekalan galas di hujung paksi kenderaan. 

Juga galas kenderaan bermotor dibentuk oleh satu atau dua gelung dalam bentuk lembu dengan pelbagai bentuk seksyen silang, di mana mereka menggulung silinder atau sfera, dengan tujuan mengurangkan geseran dalam paksi.

Dalam elektrik

Dalam aplikasi elektrik, toroid juga sangat penting, kerana nukleus ferromagnetik induktor, elektromager dan transformer, sering mempunyai bentuk lembu dan pada mereka kabel dalam bentuk gegelung.

Tokamak

Terdapat sejenis reaktor gabungan terkawal dalam bentuk toroid atau donat yang dipanggil oleh nama Rusia: tOkamak. Dalam jenis reaktor gabungan nuklear ini, bekas dan gegelung yang menghasilkan medan magnet kurungan plasma mempunyai bentuk atau pelupusan toroidal.

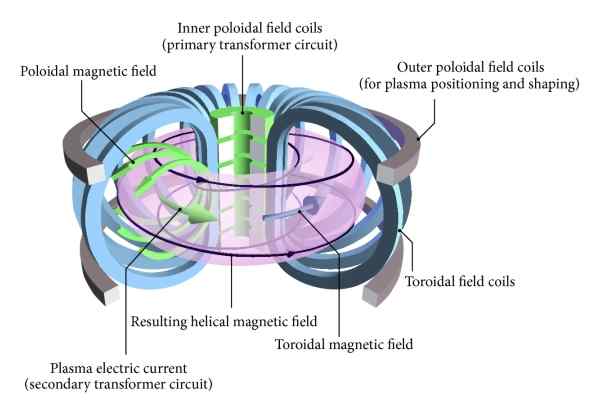Angka itu secara skematik menunjukkan reaktor gabungan nuklear terkawal dalam bentuk toroidal yang dikenali sebagai "Tokamak". Dalam jenis reaktor ini, kedua -dua plasma, gegelung dan medan magnet kurungan mempunyai konfigurasi toroidal. Sumber: Wikimedia Commons

Contoh

Permukaan Bull Square Section (oleh Formula)

Dalam contoh ini, lembu jantan persegi dianggap seperti yang ditunjukkan dalam angka berikut:

Boleh melayani anda: Segitiga Scaleno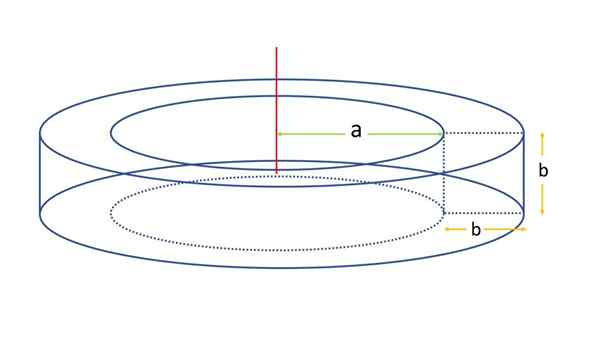 Toroid seksyen persegi. Sumber: f. Zapata

Permukaan akan ditentukan menggunakan formula permukaan untuk lembu umum. Untuk tujuan ini, perlu mengetahui jarak paksi putaran ke centroid dataran, yang menggunakan tatanama sebelumnya adalah R:

R = a + b/2

Ia juga perlu mengetahui perimeter L dari angka Generatrix, yang seperti dalam kes ini adalah persegi di sebelah b, Konturnya akan panjang:

L = 4 ⋅B

Kemudian formula permukaan lembu digunakan:

S = 2πr ⋅L

Menggantikan R dan L untuk ungkapan yang sepadan, bergantung kepada langkah A dan B dari lembu persegi adalah:

S = 2π (a + b/2) ⋅4 ⋅B = 8π (a + b/2) ⋅b

Permukaan toroid persegi (jumlah wajahnya)

Lembu persegi angka sebelumnya terdiri daripada empat muka: bahagian atas dan bawah adalah cincin rata, dan bahagian dalam dan luaran adalah silinder.

Mengambil kira ini, adalah mungkin untuk mengira permukaannya dengan menambahkan kawasan empat wajahnya.

Wajah atas dan bawah mempunyai kawasan yang sama dengan lingkaran luar jejari (A+b) kurang dari lingkaran radio dalaman ke, yang mempunyai hasilnya:

S_s= S_Yo= π [(a+b)² - b²] = π ⋅ [a²+ 2ab]

Wajah silinder dalaman mempunyai kawasan:

S₁= 2πab

Dan wajah silinder luaran mempunyai kawasan:

S₂= 2π (a+b) b = 2πab+2πB²

Jadi jumlah kawasan toroid akan menjadi jumlah s_s+S_Yo+S₁+S₂:

A = 2π ⋅ [a²+ 2ab]+2πab+2πab+2πB².