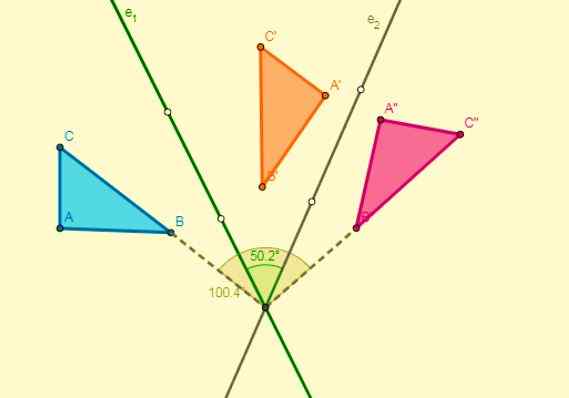
Transformasi isometrik

The transformasi isometrik Mereka adalah perubahan kedudukan atau orientasi angka tertentu yang tidak mengubah bentuk atau saiz ini. Transformasi ini diklasifikasikan kepada tiga jenis: terjemahan, putaran dan refleksi (isometri). Secara umum, transformasi geometri membolehkan membuat angka baru dari yang lain diberikan.

Transformasi ke dalam angka geometri bermakna, dalam beberapa cara, ia tertakluk kepada beberapa perubahan; iaitu, ia diubah. Mengikut rasa asal dan yang serupa dalam satah, transformasi geometri dapat diklasifikasikan kepada tiga jenis: isometrik, isomorfik dan anamorfik.

Ciri -ciri transformasi isometrik

- Transformasi isometrik berlaku apabila magnitud segmen dan sudut antara angka asal dan angka yang diubah dipelihara.

- Dalam jenis transformasi ini, bentuk atau saiz angka tidak diubah (mereka adalah kongruen), hanya perubahan kedudukan ini, sama ada dalam orientasi atau dalam erti kata. Dengan cara ini, angka awal dan final akan sama dan kongruen geometri.

- Isometri merujuk kepada kesamaan; iaitu, angka geometri akan menjadi isometrik jika mereka mempunyai bentuk dan saiz yang sama.

- Dalam transformasi isometrik, satu -satunya perkara yang dapat diperhatikan adalah perubahan kedudukan dalam satah, pergerakan tegar berlaku terima kasih yang angka itu berlalu dari kedudukan awal ke final. Angka ini dipanggil homolog (serupa) dari yang asal.

- Terdapat tiga jenis pergerakan yang mengklasifikasikan transformasi isometrik: terjemahan, putaran dan refleksi atau simetri.

Jenis transformasi isometrik

Oleh terjemahan

Adakah isometri yang membolehkan untuk menggantikan garis lurus semua titik satah dalam arah dan jarak tertentu.

Apabila angka diubah oleh terjemahan, ia tidak mengubah orientasinya berhubung dengan kedudukan awal, dan tidak kehilangan langkah dalamannya, ukuran sudut dan sisinya. Jenis anjakan ini ditakrifkan oleh tiga parameter:

• Alamat, yang boleh mendatar, menegak atau serong.
• Arah, yang boleh ke kiri, kanan, naik atau turun.
• Jarak atau magnitud, yang panjangnya dari kedudukan awal ke final dari mana -mana titik yang bergerak.

Boleh melayani anda: curtosis: definisi, jenis, formula, apa itu, contohnya

Agar transformasi isometrik disebabkan oleh terjemahan, ia mesti memenuhi syarat -syarat berikut:

• Angka itu mesti selalu menyimpan semua dimensinya, baik linear dan sudut.
• Angka ini tidak mengubah kedudukannya berkenaan dengan paksi mendatar; iaitu, sudutnya tidak pernah berubah.
• Terjemahan akan selalu diringkaskan dalam satu, tanpa mengira bilangan terjemahan yang dibuat.

Dalam satah di mana pusat adalah titik atau, dengan koordinat (0.0), terjemahan ditakrifkan oleh vektor t (a, b), yang menunjukkan anjakan titik awal. Iaitu:

P (x, y) + t (a, b) = p '(x + a, y + b)

Sebagai contoh, jika ke titik koordinat p (8, -2) terjemahan t (-4, 7) digunakan, ia diperolehi:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

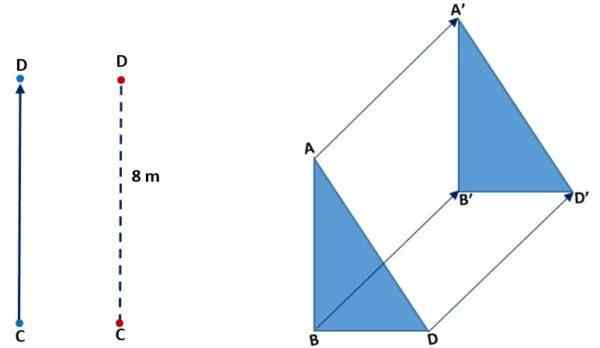
Dalam imej berikut (kiri), anda dapat melihat bagaimana titik C bergerak untuk bertepatan dengan D. Dia melakukannya secara menegak, makna naik dan jarak atau magnitud cd adalah 8 meter. Dalam imej yang betul, terjemahan segitiga diperhatikan:

Oleh putaran

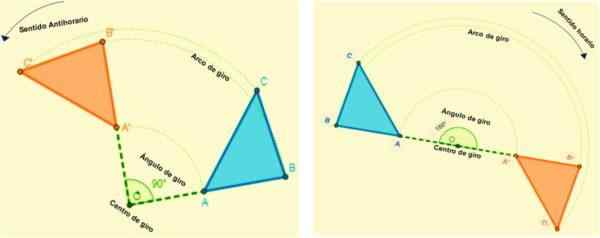
Adakah isometri yang membolehkan angka itu mengubah semua titik pesawat. Setiap titik bertukar berikutan arka yang mempunyai sudut malar dan titik tetap (pusat putaran) ditentukan.

Iaitu, semua putaran akan ditakrifkan oleh putaran dan pusat sudutnya. Apabila angka diubah oleh putaran, ia mengekalkan ukuran sudut dan sisinya.

Putaran berlaku dalam arah tertentu, adalah positif apabila gilirannya anti -horari (bertentangan dengan bagaimana tangan jam berputar) dan negatif apabila gilirannya berada dalam arah jam.

Sekiranya titik (x, y) diputar dengan asal -iaitu, pusat putarannya adalah (0.0) -, pada sudut 90^{Sama ada} 360^{Sama ada} Koordinat mata akan menjadi:

Boleh melayani anda: cawangan statistik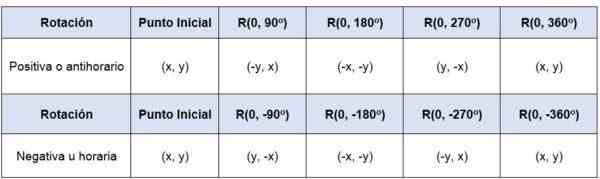

Dalam kes di mana putaran tidak mempunyai pusat pada asalnya, asal sistem koordinat ke asal yang baru harus dipindahkan, untuk memutar angka yang memiliki asal pusat.

Contohnya, jika titik p (-5,2) putaran 90 digunakan^{Sama ada}, Sekitar asal dan dalam pengertian positif koordinat baru adalah (-2,5).

Dengan refleksi atau simetri

Adalah transformasi yang melabur mata dan angka pesawat. Pelaburan ini boleh berkenaan dengan satu titik atau juga boleh berkenaan dengan garis.

Dalam erti kata lain, dalam jenis transformasi ini setiap titik dalam angka asal dikaitkan dengan titik lain (imej) angka homolog, sehingga titik dan imejnya berada pada jarak yang sama dari garis yang disebut paksi simetri.

Oleh itu, bahagian kiri angka itu akan mencerminkan sebelah kanan, tanpa mengubah bentuknya atau dimensinya. Simetri mengubah angka yang sama tetapi sebaliknya, seperti yang dapat dilihat dalam imej berikut:

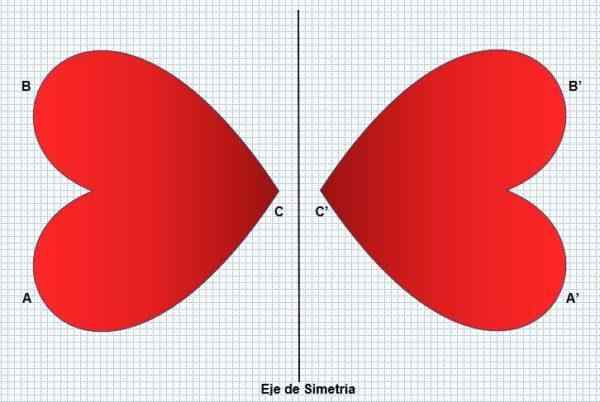
Simetri hadir dalam banyak aspek, seperti beberapa tumbuhan (bunga matahari), haiwan (merak) dan fenomena semulajadi (kepingan salji). Manusia mencerminkannya di wajahnya, yang dianggap sebagai faktor kecantikan. Refleksi atau simetri boleh mempunyai dua jenis:

Simetri pusat

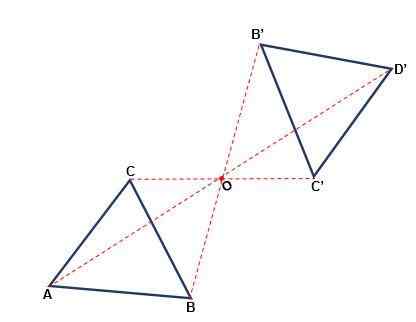
Ia adalah transformasi yang berlaku sehubungan dengan titik, di mana angka itu dapat mengubah orientasinya. Setiap titik dalam angka asal dan imejnya berada pada jarak yang sama dari satu titik atau, dipanggil pusat simetri. Simetri adalah pusat ketika:

• Kedua -dua titik dan imej dan pusatnya tergolong dalam garis yang sama.
• Dengan putaran 180^{Sama ada} dari pusat atau angka yang sama dengan asal diperoleh.
• Pukulan angka awal selari dengan pukulan angka yang terbentuk.
• Makna angka itu tidak berubah, ia akan sentiasa berada dalam jadual.

Boleh melayani anda: Berapa banyak yang perlu anda tambahkan hingga 3/4 untuk mendapatkan 6/7?

Simetri paksi

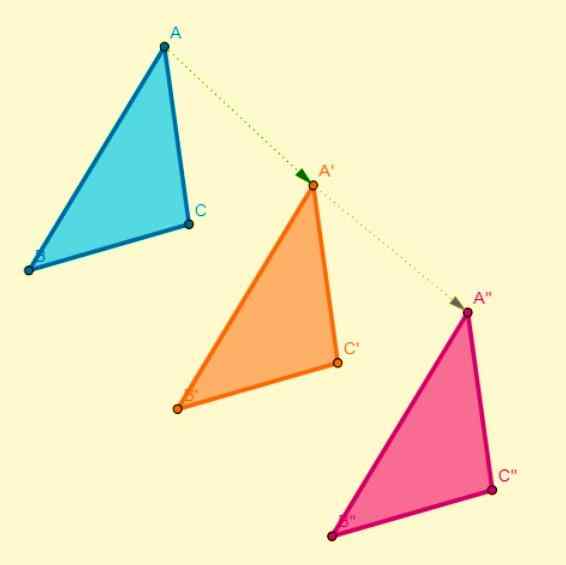
Transformasi ini berlaku berkenaan dengan paksi simetri, di mana setiap titik dalam angka awal dikaitkan dengan titik lain dalam imej dan ini berada pada jarak yang sama dengan paksi simetri. Simetri adalah paksi ketika:

• Segmen yang bergabung dengan imejnya berserenjang dengan paksi simetrinya.
• Angka -angka mengubah makna mereka mengenai arah giliran atau masa.
• Dengan membahagikan angka dengan garis tengah (paksi simetri), salah satu bahagian yang dihasilkan bertepatan sepenuhnya dengan satu lagi bahagian.

Komposisi

Komposisi transformasi isometrik merujuk kepada aplikasi transformasi isometrik berturut -turut pada angka yang sama.

Komposisi terjemahan

Komposisi dua terjemahan menghasilkan terjemahan lain. Apabila dilakukan pada satah, pada paksi mendatar (x) hanya koordinat perubahan paksi itu, sementara koordinat paksi menegak (y) tetap sama, dan sebaliknya.

Komposisi putaran

Komposisi dua giliran dengan hasil pusat yang sama pada giliran yang lain, yang mempunyai pusat yang sama dan amplitudnya akan menjadi jumlah amplitud kedua -dua giliran.

Sekiranya pusat gilirannya mempunyai pusat yang berbeza, potongan dua segmen titik serupa akan menjadi pusat putaran.

Komposisi simetri

Dalam kes ini, komposisi akan bergantung pada bagaimana ia digunakan:

• Sekiranya simetri yang sama digunakan dua kali, hasilnya akan menjadi identiti.
• Jika dua simetri digunakan berkenaan dengan dua paksi selari, hasilnya akan terjemahan, dan anjakan mereka adalah dua kali jarak dari paksi tersebut:

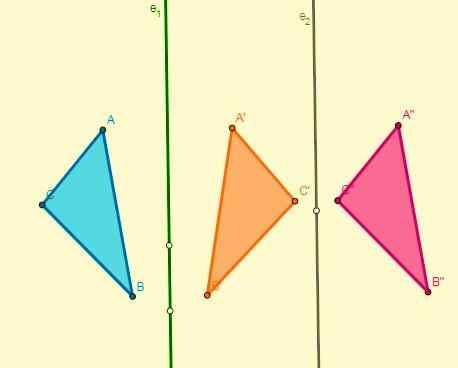
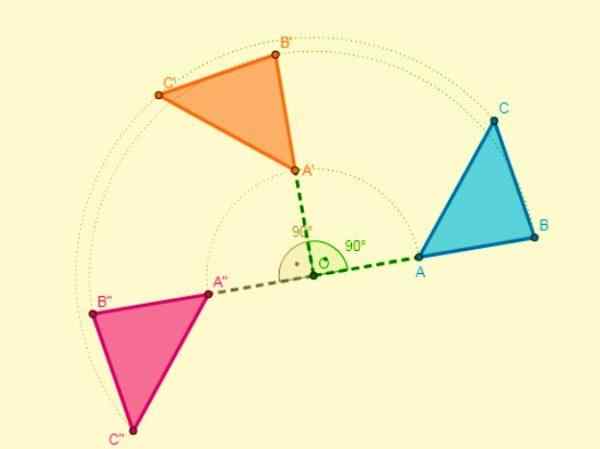
• Jika dua simetri digunakan dengan dua paksi yang dipotong pada titik O (pusat), putaran dengan pusat akan diperoleh dan sudutnya akan menjadi dua kali sudut yang bentuk paksi: