Homotecia

The Homotecia Ia adalah perubahan geometri dalam satah di mana, dari titik tetap yang dipanggil pusat (o), jarak didarab dengan faktor biasa. Dengan cara ini, setiap titik P sepadan dengan titik lain transformasi, dan ini sejajar dengan titik atau.

Kemudian, homotecia adalah surat -menyurat antara dua angka geometri, di mana titik yang diubah dipanggil homothetic, dan ini sejajar dengan titik tetap dan dengan segmen selari antara satu sama lain.

Penjelasan dan Formula

Homotecia adalah transformasi yang tidak mempunyai imej kongruen, kerana dari angka mereka akan memperoleh satu atau lebih angka saiz yang lebih besar atau lebih rendah daripada angka asal; iaitu, Homotecia mengubah poligon menjadi yang serupa.

Agar homotecia dipenuhi, titik ke titik dan garis lurus mesti sesuai, supaya pasangan titik homolog diselaraskan dengan titik tetap ketiga, yang merupakan pusat homotecia.

Begitu juga, pasangan garis yang bersatu harus selari. Hubungan antara segmen sedemikian adalah alasan yang dipanggil homotecia (k) yang tetap; sedemikian rupa sehingga homotecia dapat ditakrifkan sebagai:

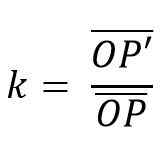
Untuk menjadikan jenis transformasi ini, titik sewenang -wenangnya bermula, yang akan menjadi pusat homotecia.

Dari sudut ini, segmen garis ditarik untuk setiap puncak angka yang akan diubah. Skala di mana pembiakan angka baru dibuat untuk alasan homotecia (k).

Homotecia Properties

Salah satu sifat utama homotecia ialah, atas alasan homotecia (k), semua angka homothetik adalah serupa. Antara harta tertunggak yang lain adalah seperti berikut:

Ia boleh melayani anda: Kompaun berkadar: Penjelasan, tiga peraturan kompaun, latihan

- Pusat Homotecia (O) adalah satu -satunya titik ganda dan ia mengubah dirinya sendiri; iaitu, ia tidak berbeza.

- Garis yang melewati pusat menjadi diri mereka sendiri (mereka berganda), tetapi titik -titik yang mengarangnya tidak berganda.

- Garis yang tidak melalui pusat berubah menjadi garis selari; Dengan cara ini, sudut homotecia tetap sama.

- Imej segmen oleh homotecia tengah atau dan sebab k, adalah segmen selari dengannya dan mempunyai kali panjangnya. Sebagai contoh, seperti yang dilihat dalam imej berikut, segmen AB untuk homotecia akan menjadi segmen A'b lain ', supaya ab akan selari dengan A'B' dan K akan menjadi:

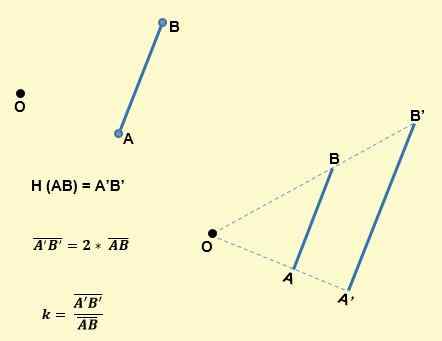
- Sudut homotetik adalah kongruen; iaitu, mereka mempunyai ukuran yang sama. Oleh itu, imej sudut adalah sudut yang mempunyai amplitud yang sama.

Sebaliknya, homotecia perlu diubah bergantung pada nilai sebabnya (k), dan kes -kes berikut mungkin berlaku:

- Sekiranya malar k = 1, semua mata ditetapkan kerana mereka mengubah diri mereka. Oleh itu, angka homotetik bertepatan dengan asal dan transformasi akan dipanggil fungsi identiti.

- Jika k ≠ 1, satu -satunya titik tetap akan menjadi pusat homotecia (O).

- Jika k = -1, homotecia menjadi simetri pusat (c); Iaitu, putaran akan berlaku di sekitar c, pada sudut 180^{Sama ada}.

- Sekiranya k> 1, saiz angka yang diubah akan lebih besar kepada saiz asal.

Boleh melayani anda: nombor yang tidak rasional: sejarah, sifat, klasifikasi, contoh

- Ya 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.

- Ya -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

- Ya k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Jenis Homotecia

Homotecia juga boleh diklasifikasikan kepada dua jenis, bergantung kepada nilai sebabnya (k):

Homotecia langsung

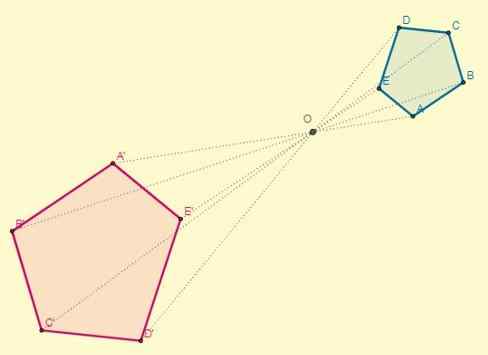
Berlaku jika tetap k> 0; Iaitu, titik homotetik berada di sisi yang sama berkenaan dengan pusat:

Faktor perkadaran atau nisbah persamaan antara angka homothetik langsung akan sentiasa positif.

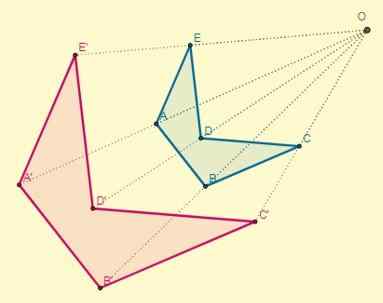
Homotecia songsang

Berlaku jika kaum k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

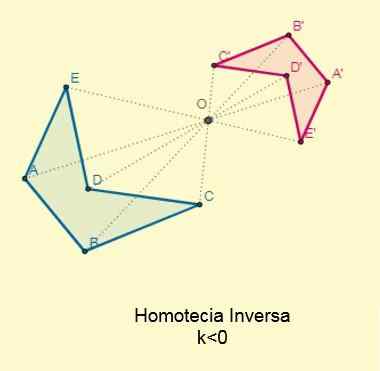
Faktor perkadaran atau nisbah persamaan antara angka homothetik songsang akan sentiasa negatif.

Komposisi

Apabila beberapa pergerakan dijalankan secara berturut -turut sehingga angka sama dengan yang asal, komposisi pergerakan berlaku. Komposisi beberapa pergerakan juga merupakan pergerakan.

Komposisi antara dua homotecia menghasilkan homotecia baru; Ia.

Oleh itu, dalam komposisi dua homoties h₁(Sama ada₁, k₁) dan h₂(Sama ada₂, k₂), Pendaraban sebab anda: k₁ x k₂ = 1 akan menghasilkan homotecia sebab k₃ = K₁ x k₂. Pusat homotecia baru ini (atau₃) akan terletak di barisan atau₁ Sama ada₂.

Ia dapat melayani anda: sudut bertentangan dengan puncak (dengan senaman yang diselesaikan)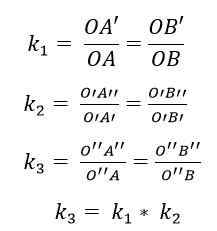

Homotecia sepadan dengan perubahan yang rata dan tidak dapat dipulihkan; Sekiranya dua homotekia memohon yang mempunyai pusat dan alasan yang sama tetapi dengan tanda yang berbeza, angka asal akan diperolehi.

Contoh Homotecia

1. Contoh pertama

Sapukan Homotecia ke Poligon Pusat (O) yang diberikan, terletak 5 cm dari titik A dan alasannya adalah k = 0.7.

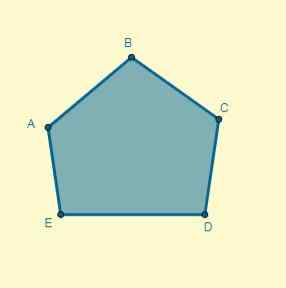
Penyelesaian

Mana -mana titik dipilih sebagai pusat homotecia, dan dari ini mereka didagangkan oleh simpul angka:

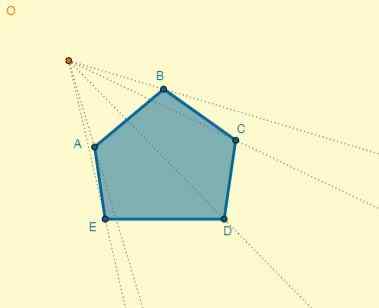
Jarak dari pusat (O) ke titik A adalah OA = 5; Dengan ini anda boleh menentukan jarak salah satu titik homotetik (OA ') juga mengetahui bahawa k = 0.7:

Oa '= k x oa.

Oa '= 0.7 x 5 = 3.5.

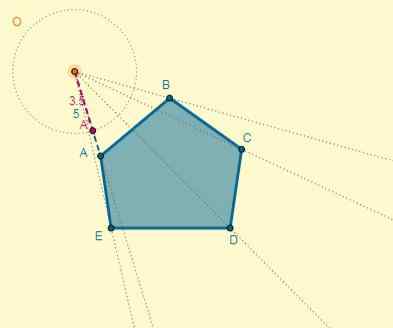
Proses ini boleh dilakukan untuk setiap puncak, atau anda juga boleh menarik poligon homothetik yang mengingati bahawa kedua -dua poligon mempunyai sisi selari:

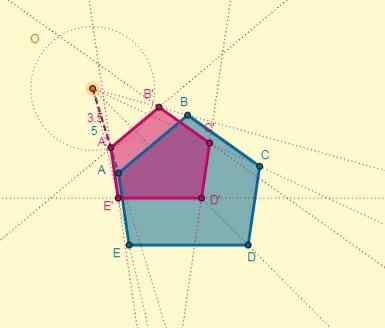
Akhirnya, transformasi dilihat seperti berikut:

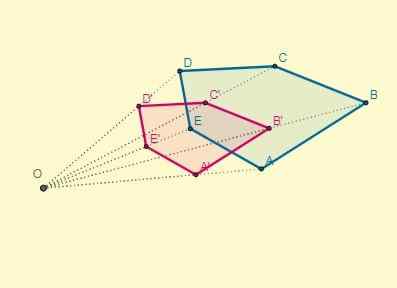
2. Contoh kedua

Sapukan Homotecia ke Poligon Pusat (O) yang diberikan, terletak 8.5 cm dari titik C dan yang dan sebabnya k = -2.

Penyelesaian

Jarak dari pusat (O) ke titik C ialah OC = 8.5; Dengan data ini adalah mungkin untuk menentukan jarak salah satu titik homotetik (OC '), juga mengetahui bahawa k = -2:

Oc '= k x oc.

Oc '= -2 x 8.5 = -17

Selepas melukis segmen simpul poligon yang diubah, titik awal dan homotetik mereka terletak di hujung yang bertentangan dengan pusat: