Fourier Transformed Properties, Aplikasi, Contoh

The Fourier bijak berubah Ini adalah kaedah berangka yang digunakan untuk menentukan sampel yang berkaitan dengan frekuensi spektrum yang membentuk isyarat. Kajian fungsi berkala dalam parameter tertutup, membuang sebagai hasilnya isyarat yang bijak.

Untuk mendapatkan transformasi Furier dari titik N, pada isyarat yang bijak, 2 syarat berikut pada urutan mesti dipenuhi X [n]

 x [n] = 0   N n - 1

Memenuhi syarat -syarat ini, transformasi diskret Fourier dapat ditakrifkan sebagai

Tdf

Transformasi bijak Fourier dapat ditakrifkan sebagai pensampelan di titik N Fourier Transform.

[TOC]

Tafsiran Transformasi Berhati -hati Fourier

Sumber: Pexels

Terdapat 2 titik pandangan dari mana hasil yang diperoleh pada urutan x dapat ditafsirkan_s[n] melalui transformasi yang bijak Fourier.

-Yang pertama sepadan dengan pekali spektrum, sudah diketahui siri Fourier. Ia diperhatikan dalam isyarat berkala diskret, dengan sampel bertepatan dengan urutan x_s[N].

-Yang kedua adalah mengenai spektrum isyarat aperiadik yang bijak, dengan sampel yang sepadan dengan urutan x_s[N].

Transformasi yang bijak adalah pendekatan kepada spektrum isyarat analog asal. Fasa bergantung pada detik -detik pensampelan, sementara magnitudnya bergantung pada selang persampelan.

Sifat

Asas struktur algebra membentuk asas logik dari bahagian berikut.

Linearity

C . S_n → c . F [S_k]; Sekiranya urutan didarabkan oleh skalar, transformasi juga akan.

T_n + V_n = F [t_k]+F [v_k]; Transformasi jumlah sama dengan jumlah yang berubah.

Duality

F [s_n] → (1/n) s_-K; Sekiranya transformasi Fourier yang bijak ditarik balik kepada ungkapan yang sudah berubah, ungkapan yang sama diperolehi, memanjat n terbalik dengan paksi menegak.

Convolution

Mengejar objektif yang sama yang dalam perubahan Laplace, konvolusi fungsi merujuk kepada produk di antara Fourier Transforms. Convolution juga terpakai untuk masa diskret dan bertanggungjawab untuk banyak prosedur moden.

X_n * R_n → F [x_n] .F [r_n]; Transformasi konvolusi adalah sama dengan produk yang diubah.

X_n . R_n→ F [x_n] * F [r_n]; Transformasi produk adalah sama dengan konvolusi yang berubah.

Pemindahan

X_N-m → F [x_k] e ^{-I (2π/n) km} ; Sekiranya penggantian ditangguhkan dalam sampel m, kesannya terhadap transformasi yang bijak akan menjadi pengubahsuaian sudut yang ditakrifkan oleh (2π/n) km.

Boleh melayani anda: mengapa algebra penting dalam situasi kehidupan seharian tertentu?

Simetri Konjugasi

X_t [-K] = x*_t[k] = x_t [N - k]

Modulasi

W^-nm_N . x [n] ↔ x_t[K - m]

Produk

x [n] y [n] ↔ (1/n) x_t[k]*dan_t[K]

Simetri

X [-n] ↔ x_t[-K] = x*_t[K]

Conjugate

x*[n] ↔ x*_t[-K]

Persamaan parseval 

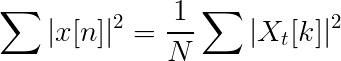
Persamaan dan perbezaan dengan transformasi Fourier

Berkenaan dengan transformal konvensional Fourier, ia mempunyai beberapa persamaan dan perbezaan. Transformasi Fourier menukarkan urutan menjadi garis berterusan. Dengan cara ini dikatakan bahawa hasil pembolehubah Fourier adalah fungsi pembolehubah sebenar yang kompleks.

Transformasi bijak Fourier, tidak seperti, menerima isyarat bijak dan mengubahnya menjadi tanda yang bijak, iaitu urutan.

Apakah penggunaan transformasi yang bijak Fourier?

Mereka terutamanya berkhidmat dengan persamaan yang signifikan, sambil mengubah ungkapan yang diperolehi menjadi elemen kuasa. Menandakan ungkapan pembezaan dalam bentuk polinomial yang boleh dipercayai.

Dalam pengoptimuman, modulasi dan pemodelan hasil ia bertindak sebagai ungkapan piawai, menjadi sumber yang kerap untuk kejuruteraan selepas beberapa generasi.

Sumber: Pixabay

Sejarah

Konsep matematik ini disampaikan oleh Joseph B. Fourier pada tahun 1811, sambil membangunkan perjanjian mengenai Penyebaran haba. Ia dengan cepat diterima oleh pelbagai cabang sains dan kejuruteraan.

Ia ditubuhkan sebagai alat kerja utama dalam kajian persamaan dengan derivatif separa, membandingkan walaupun dengan hubungan kerja antara Laplace berubah dan persamaan pembezaan biasa.

Sebarang fungsi yang boleh dilakukan dengan transformasi Fourier mesti membentangkan pembatalan di luar parameter yang ditetapkan.

Fourier bijak berubah dan terbalik

Transformasi yang bijak diperoleh melalui ungkapan:

Selepas urutan yang bijak x [n]

Kebalikan dari Transformasi Berdiri Fourier ditakrifkan melalui ungkapan:

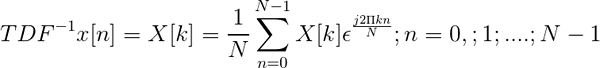TDF songsang

Ia membolehkan apabila ditukar dengan bijak, tentukan urutan dalam domain masa x [n].

Barang kemas

Proses parameterisasi yang sepadan dengan transformasi diskret Fourier terletak pada cub. Untuk mengatasi perubahan, kita mesti mengehadkan urutan dalam masa. Dalam banyak kes, isyarat yang dipersoalkan tidak mempunyai batasan ini.

Penggantian yang tidak memenuhi kriteria saiz untuk memohon kepada transformasi yang bijak, boleh didarabkan dengan fungsi "tetingkap" v [n], menentukan tingkah laku penggantian dalam parameter terkawal.

Boleh melayani anda: permutasi bulat: demonstrasi, contoh, latihan yang diselesaikan

X [n] . V [n]

Lebar spektrum akan bergantung pada lebar tetingkap. Apabila lebar tetingkap meningkat, perubahan yang dikira akan lebih sempit.

Aplikasi

Pengiraan penyelesaian asas

Transformasi bijak Fourier adalah alat yang berkuasa dalam kajian penggantian diskret.

Transformasi yang bijak Fourier mengubah fungsi pemboleh ubah yang berterusan, menjadi transformasi pemboleh ubah diskret.

Masalah Cauchy untuk persamaan haba membentangkan bidang yang kerap digunakan untuk transformasi Fourier yang bijak. Di mana fungsi dijana Dirichlet panas atau nukleus teras, yang digunakan untuk pensampelan nilai dalam parameter yang ditetapkan.

Teori isyarat

Alasan umum untuk permohonan transformasi diskret Fourier di cawangan ini kebanyakannya disebabkan oleh penguraian ciri isyarat sebagai pertindihan tak terhingga dari isyarat yang lebih mudah dirawat.

Ia boleh menjadi gelombang bunyi atau gelombang elektromagnet, transformasi diskret Fourier mengekspresikannya dalam gelombang mudah bertindih. Perwakilan ini agak kerap dalam kejuruteraan elektrik.

Siri Fourier

Mereka ditakrifkan siri dari segi cosenos dan payudara. Mereka berkhidmat untuk memudahkan kerja dengan fungsi berkala umum. Apabila digunakan, mereka adalah sebahagian daripada teknik penyelesaian persamaan pembezaan separa dan biasa.

Siri Fourier lebih umum daripada siri Taylor, kerana mereka membangunkan fungsi Discontinua berkala yang tidak mempunyai perwakilan dalam siri Taylor.

Bentuk lain dalam siri Fourier

Secara analitik memahami perubahan Fourier, ia penting.

-Siri Fourier pada Fungsi Tempoh 2L:

Ramai kali perlu menyesuaikan struktur siri Fourier, ke fungsi berkala yang tempohnya P = 2L> 0 dalam selang [-L, L].

-Siri Fourier dalam fungsi Even dan Ganjil

Selang [-π, π] dianggap yang menawarkan kelebihan apabila memanfaatkan ciri-ciri simetri fungsi.

Boleh melayani anda: set terhingga: sifat, contoh, latihan yang diselesaikan

Sekiranya F adalah tork Siri Fourier ditubuhkan sebagai satu siri Cosenos.

Sekiranya F adalah ganjil, siri Fourier ditubuhkan sebagai satu siri payudara.

-Notasi kompleks siri Fourier

Jika anda mempunyai fungsi F (t), yang memenuhi semua keperluan siri Fourier, adalah mungkin untuk menunjukkannya dalam selang [-t, t] menggunakan notasi kompleksnya: 

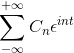
Contoh

Mengenai pengiraan penyelesaian asas, contoh -contoh berikut dibentangkan:

Persamaan Laplace

Persamaan haba

Persamaan Schrödinger

Persamaan Gelombang

Sebaliknya, terdapat contoh -contoh penggunaan transformasi diskret Fourier dalam bidang teori isyarat:

-Masalah pengenalan sistem. Ditubuhkan f dan g

-Masalah dengan konsistensi isyarat output

-Masalah dengan penapisan isyarat

Latihan

Latihan 1

Kirakan transformasi yang bijak Fourier untuk penggantian berikut.

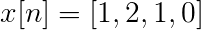
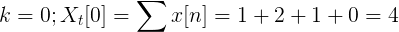
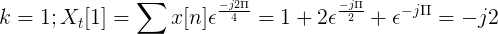
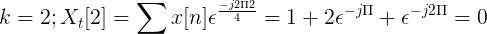
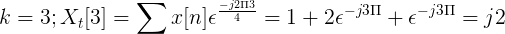
TDF x [n] boleh ditakrifkan sebagai:

X_t[k] = 4, -j2, 0, j2 untuk k = 0, 1, 2, 3

Latihan 2

Ia mahu menentukan melalui algoritma digital isyarat spektrum yang ditakrifkan oleh ekspresi x (t) = e^-t. Di mana frekuensi maksimum yang meminta pekali adalah f_m= 1Hz. Harmonik sepadan dengan F = 0.3 Hz. Kesalahannya terhad kepada kurang daripada 5%. Hitung F_s , D dan n.

Dengan mengambil kira teorem persampelan F_s = 2f_m = 2 Hz

Resolusi kekerapan F₀ = 0.1 Hz, di mana d = 1/0.1 = 10s diperoleh

0.3 Hz adalah kekerapan yang sepadan dengan indeks k = 3, di mana n = 3 × 8 = 24 pensampelan. Menunjukkan bahawa F_s = N/d = 24/10 = 2.4> 2

Kerana tujuannya adalah untuk mencapai nilai yang paling sedikit untuk n, nilai -nilai berikut dapat dianggap sebagai penyelesaian:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33s

K = 1

N = 1 × 8 = 8

Rujukan

1. Menguasai transformasi Fourier diskret dalam satu, dua atau beberapa dimensi: perangkap dan artifak. Isaac Amidor. Springer Science & Business Media, 19 Julai. 2013
2. DFT: Manual Pemilik untuk Transformasi Fourier Diskret. William l. Briggs, Van Emden Henson. Siam, 1 Januari. Sembilan-belas sembilan puluh lima
3. Pemprosesan Isyarat Digital: Teori dan Amalan. D. Sundararajan. Saintifik Dunia, 2003
4. Mengubah dan Algoritma Cepat untuk Analisis dan Perwakilan Isyarat. Guoan BI, Yonghong Zeng. Springer Science & Business Media, 6 Disember. 2012
5. Transformasi Fourier yang diskret dan berterusan: Analisis, Aplikasi dan Algoritma Cepat. Eleanor Chu. CRC Press, 19. 2008