Segitiga Acutangle

Apakah segitiga acutangulus?

The Segitiga Acutangulus Mereka adalah mereka yang tiga sudut dalaman adalah sudut akut; iaitu, ukuran setiap sudut itu kurang dari 90 ° darjah. Dengan tidak mempunyai sudut yang betul, kita mempunyai teorem Pythagoras tidak dipenuhi untuk angka geometri ini.

Oleh itu, jika kita ingin mempunyai beberapa jenis maklumat mengenai mana -mana sisi atau sudutnya, perlu menggunakan teorema lain yang membolehkan kita mempunyai akses kepada data ini. Mereka yang boleh kita gunakan adalah teorem payudara dan teorem kosinus.

Ciri -ciri segitiga acutangle

Antara ciri -ciri yang dimiliki oleh angka geometri ini, kita dapat menyerlahkan mereka yang diberikan oleh fakta mudah menjadi segitiga. Antara ini kita perlu:

- Segitiga adalah poligon yang mempunyai tiga sisi dan tiga sudut.

- Jumlah tiga sudut dalamannya sama dengan 180 °.

- Jumlah dua sisinya selalu lebih besar daripada yang ketiga.

Sebagai contoh, mari kita lihat segitiga ABC berikut. Secara umum, kami mengenal pasti sisi mereka dengan huruf kecil dan sudut mereka dengan huruf besar, sehingga sisi dan sudut bertentangan mereka mempunyai huruf yang sama.

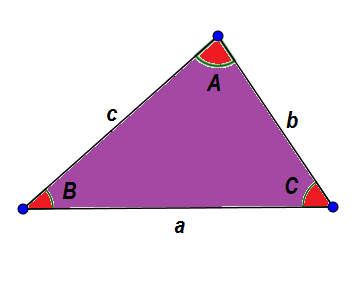
Kerana ciri -ciri yang telah diberikan, kita tahu bahawa:

A + B + C = 180 °

A + b> c, a + c> b dan b + c> a

Ciri -ciri utama yang membezakan jenis segitiga ini dari selebihnya ialah, seperti yang telah kita sebutkan, sudut dalamannya adalah akut; iaitu ukuran setiap sudutnya kurang dari 90 °.

Segitiga Acutangulus, bersama -sama dengan segitiga bodoh (yang mana salah satu sudutnya mempunyai ukuran yang lebih besar daripada 90 °), adalah sebahagian daripada segitiga serong yang ditetapkan. Set ini dibentuk oleh segitiga yang bukan segi empat tepat.

Boleh melayani anda: apakah unsur -unsur perumpamaan? (Bahagian)

Dengan menjadi sebahagian daripada segitiga serong, kita perlu menyelesaikan masalah di mana segitiga acutangulus campur tangan mesti menggunakan teorem payudara dan teorem kosinus.

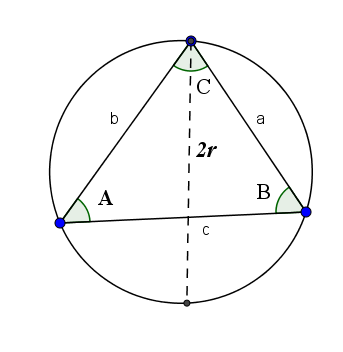
Teorem Payudara

Teorem Payudara menegaskan bahawa alasan di satu sisi dengan pangkuan sudut bertentangannya adalah sama dengan dua kali jejari bulatan yang dibentuk oleh tiga simpang segitiga tersebut. Iaitu:

2R = A/sin (a) = b/sen (b) = c/sen (c)

Teorem Coseno

Sebaliknya, teorem Coseno memberi kita tiga persamaan untuk mana -mana segitiga ABC:

ke²= b² + c² -2bc*cos (a)

b²= a² + c² -2ac*cos (b)

c²= a² + b² -2ab*cos (c)

Teorema ini juga dikenali sebagai Undang -Undang Sinus dan Undang -Undang Cosine, masing -masing.

Satu lagi ciri yang boleh kita berikan dari segi tiga yang akut adalah bahawa dua daripadanya adalah sama jika mereka memenuhi mana -mana kriteria berikut:

• Sekiranya mereka mempunyai ketiga -tiga belah pihak.
• Sekiranya mereka mempunyai sisi dan dua sudut sama antara satu sama lain.
• Sekiranya mereka mempunyai dua sisi dan sudut yang sama.

Jenis Segitiga Acutángulos

Segitiga Acutangulus dapat diklasifikasikan mengikut sisi mereka. Ini mungkin:

Segitiga acutangulos sama

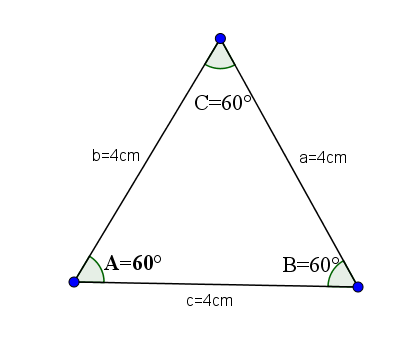
Mereka adalah segitiga akut yang mempunyai semua sisi yang sama dan, oleh itu, semua sudut dalaman mereka mempunyai nilai yang sama, iaitu A = B = C = 60 ° darjah.

Sebagai contoh, mari kita ambil segitiga berikut, yang sisi A, B dan C mempunyai nilai 4.

Isosceles acutángulos segitiga

Segitiga ini, sebagai tambahan kepada sudut dalaman yang akut, mempunyai ciri -ciri mempunyai dua sisi yang sama dan yang ketiga, yang umumnya diambil sebagai pangkalan, berbeza.

Contoh jenis segitiga jenis ini boleh menjadi satu asasnya 3 dan kedua -dua belahnya mempunyai nilai 5. Dengan langkah -langkah ini, ia akan mempunyai sudut yang bertentangan dengan sisi yang sama dengan nilai 72.55 ° dan sudut bertentangan pangkalannya ialah 34.9 °.

Boleh melayani anda: sudut null: definisi dan ciri, contoh, latihan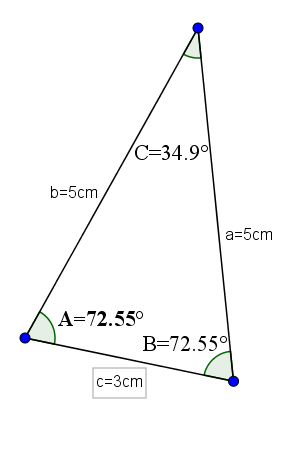

SCALENE ACUTANGULUS Segitiga

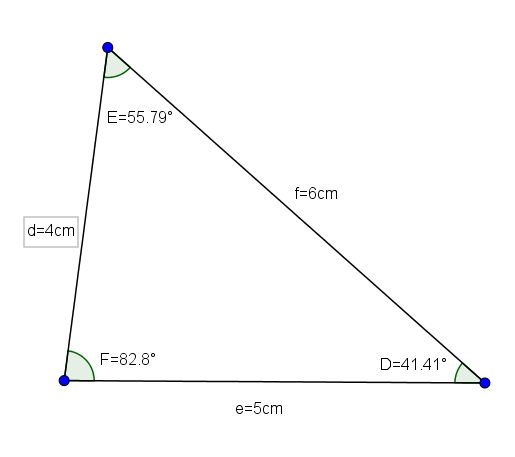
Ini adalah segitiga yang mempunyai semua pihak yang berbeza dua hingga dua. Oleh itu, semua sudutnya, sebagai tambahan kepada kurang daripada 90 °, berbeza dua hingga dua.

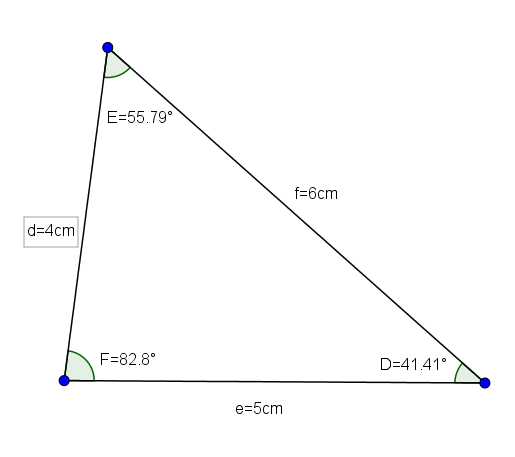
Segitiga def (langkah -langkah yang d = 4, e = 5 dan f = 6 dan sudutnya adalah d = 41.41 °, E = 55.79 ° dan F = 82.8 °) adalah contoh yang baik dari scalene segitiga acutangle.

Resolusi segitiga acutangles

Seperti yang kita katakan sebelum ini, untuk penyelesaian masalah di mana segitiga acutangulus campur tangan.

Contoh 1

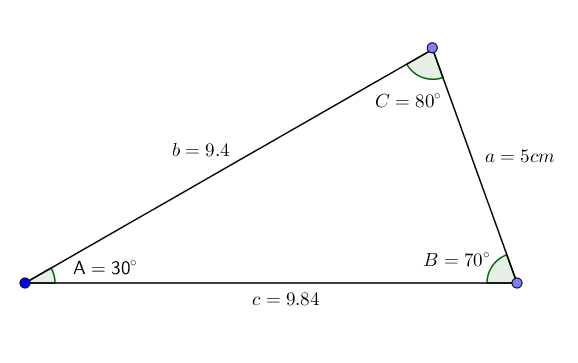
Memandangkan segitiga ABC dengan sudut A = 30 °, B = 70 ° dan sisi A = 5cm, kita ingin mengetahui nilai sudut C dan sisi B dan C.

Perkara pertama yang kita lakukan ialah menggunakan hakikat bahawa jumlah sudut dalaman segitiga adalah 180 °, untuk mendapatkan nilai sudut c.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Kami membersihkan C dan kami ada:

C = 180 ° - 100 ° = 80 °

Seperti yang kita ketahui tiga sudut dan satu sisi, kita boleh menggunakan teorem payudara untuk menentukan nilai baki sisi. Untuk teorem kita perlu:

a/sin (a) = b/sen (b) dan a/sen (a) = c/(dosa (c)

Kami membersihkan persamaan dan kita perlu:

B = (a*sin (b))/sin (a) ≈ (5*0.940) / (0.5) ≈ 9.4

Sekarang kita hanya perlu mengira nilai c. Kami meneruskan analog seperti dalam kes sebelumnya:

C = (a*sin (c))/sin (a) ≈ (5*0.984)/(0.5) ≈ 9.84

Oleh itu kita mendapat semua data segitiga. Seperti yang dapat kita perhatikan, segitiga ini memasuki kategori segitiga pengimbasan.

Contoh 2

Memandangkan segitiga pertahanan dengan sisi d = 4cm, e = 5cm dan f = 6cm, kami ingin mengetahui nilai sudut segitiga tersebut.

Untuk kes ini kita akan menggunakan undang -undang kosinus, yang memberitahu kita bahawa:

Boleh melayani anda: jumlah kuadrat dua nombor berturut -turut

d²= e² + F² - 2efcos (d)

Dari persamaan ini kita dapat membersihkan COS (d), yang menghasilkan:

Cos (d) = ((4)² - (5)² -(6)²)/(-2*5*6) = 0.75

Dari sini kita mesti berlabuh 41.41 °

Menggunakan Teorem Senom Sekarang kita mempunyai persamaan berikut:

D/(dosa (d) = e/(sin (e)

Membersihkan sen (e), kita perlu:

dosa (e) = e*sen (d)/d = (5*0.66)/4 ≈ 0.827

Dari sini kita mesti.79 °

Akhirnya, dengan menggunakan jumlah sudut dalaman segitiga adalah 180 °, kita harus.8 °.