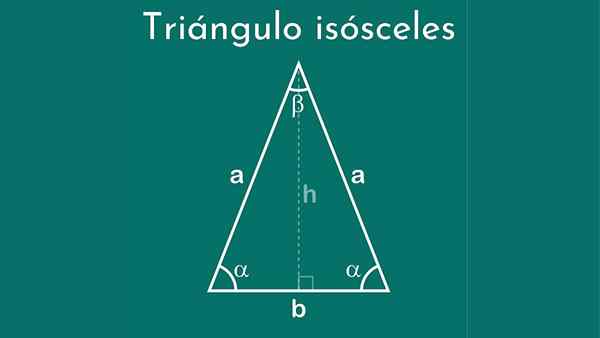
Segitiga Isosceles

Segitiga Isosceles mempunyai dua sisi yang sama dan satu berbeza

Apa itu segitiga isosceles?

A Segitiga Isosceles Ia adalah poligon tiga yang berpandu, di mana dua daripadanya mempunyai ukuran yang sama dan sisi ketiga ukuran yang berbeza. Bahagian terakhir ini dipanggil asas. Oleh kerana ciri ini nama ini diberikan, yang dalam bahasa Yunani bermaksud "kaki yang sama".

Segitiga adalah poligon yang dianggap sebagai yang paling mudah dalam geometri, kerana ia dibentuk oleh tiga sisi, tiga sudut dan tiga titik. Mereka adalah orang yang mempunyai bilangan sisinya dan sudut yang paling sedikit berkenaan dengan poligon lain, namun penggunaannya sangat luas.

Ciri -ciri segitiga isosceles

Segitiga Isosceles diklasifikasikan menggunakan ukuran sisinya sebagai parameter, kerana dua sisinya adalah kongruen, iaitu, mereka mempunyai panjang yang sama.

Menurut amplitud sudut dalaman, segitiga isosceles diklasifikasikan sebagai:

• Segitiga segi empat tepat isosceles: Dua sisinya sama. Salah satu sudutnya lurus (90^{Sama ada}) Dan yang lain adalah sama (45^{Sama ada} masing -masing)
• Isosceles segitiga: Dua sisinya sama. Salah satu sudutnya adalah bodoh (> 90^{Sama ada}).
• Isosceles acutangle Triangle: Dua sisinya sama. Semua sudutnya akut (< 90^{Sama ada}), Di mana dua mempunyai ukuran yang sama.

Komponen

• Median: Ia adalah garis yang meninggalkan dari titik tengah di satu sisi dan mencapai puncak yang bertentangan. Tiga medium itu hadir pada titik yang dipanggil Baricentro atau Centroid.
• Bisektor: Ia adalah separuh yang membahagikan sudut setiap puncak ke dalam dua sudut ukuran yang sama. Itulah sebabnya ia dikenali sebagai paksi simetri, dan jenis segitiga ini hanya mempunyai satu.
• The Mediatrix: Ia adalah segmen tegak lurus ke sisi segitiga, yang berasal dari tengah -tengah ini. Terdapat tiga mediasi di segitiga dan menghadiri titik yang disebut circumcentro.
• Ketinggian: Ia adalah garis yang pergi dari puncak ke sisi yang bertentangan dan juga garis ini berserenjang ke sisi itu. Semua segitiga mempunyai tiga ketinggian, yang bertepatan pada titik yang dipanggil Ortocenter.

Isosceles Triangles Properties

Segitiga isosceles ditakrifkan atau dikenal pasti kerana mereka mempunyai beberapa sifat yang mewakili mereka, berasal dari teorem yang dicadangkan oleh ahli matematik yang hebat:

Sudut dalaman

Jumlah sudut dalaman selalu sama dengan 180^{Sama ada}.

Jumlah sisi

Jumlah ukuran dua pihak harus selalu lebih besar daripada ukuran sisi ketiga, a + b> c.

Sisi kongruen

Segitiga isosceles mempunyai dua sisi dengan ukuran atau panjang yang sama; iaitu, mereka adalah kongruen, dan pihak ketiga berbeza dari ini.

Sudut kongruen

Segitiga isosceles juga dikenali sebagai segitiga isoangulous, kerana mereka mempunyai dua sudut yang mempunyai ukuran yang sama (kongruen). Ini terletak di pangkal segitiga, menentang sisi yang mempunyai panjang yang sama.

Boleh melayani anda: prisma trapezoid

Kerana ini, teorem yang menetapkan bahawa:

"Jika segitiga mempunyai dua sisi kongruen, sudut yang menentang pihak tersebut juga akan menjadi kongruen". Oleh itu, jika segitiga adalah isosceles sudut pangkalannya adalah kongruen.

Contoh:

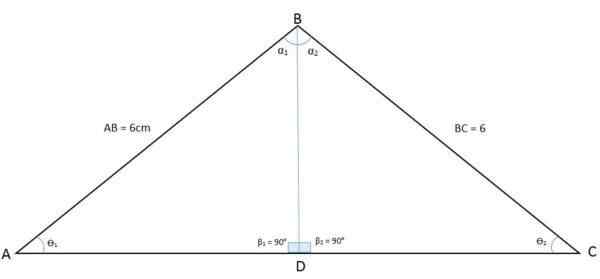
Dalam angka berikut, segitiga ABC diperhatikan. Apabila melukis bisektornya dari puncak sudut B ke pangkalan, segitiga dibahagikan kepada dua segitiga BDA dan BDC:

Bisektor yang membahagikan dua segitiga sama dengan segitiga isosceles

Dengan cara ini, sudut puncak B juga dibahagikan kepada dua sudut yang sama. Bisektor kini menjadi bahagian biasa (BD) di antara kedua -dua segitiga baru, sementara sisi AB dan BC adalah sisi kongruen. Ini adalah kes sampingan, sudut, sisi (lal).

Itu menunjukkan bahawa sudut simpang A dan C mempunyai ukuran yang sama, dan juga dapat ditunjukkan bahawa sebagai segitiga BDA dan BDC adalah kongruen, sisi AD dan DC juga.

Ketinggian, median, meditrix dan bisector adalah kebetulan

Garis yang diambil dari puncak yang bertentangan dengan pangkal ke titik tengah asas segitiga isosceles, pada masa yang sama ketinggian, median dan meditrix, serta bisector relatif ke sudut bertentangan.

Semua segmen ini bertepatan dengan yang mewakili mereka.

Contoh:

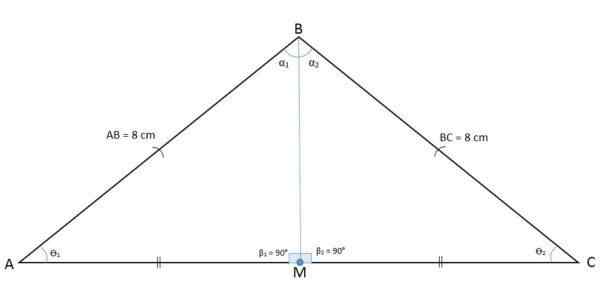
Dalam angka berikut, segitiga ABC diperhatikan dengan titik m sederhana yang membahagikan pangkalannya menjadi dua segmen BM dan CM.

Ketinggian, median, meditrix dan bisector adalah kebetulan

Semasa melukis segmen dari titik m ke puncak yang bertentangan, dengan definisi median AM diperolehi, yang relatif kepada puncak A dan ke sisi BC.

Memandangkan segmen AM membahagikan segitiga ABC menjadi dua segitiga yang sama amb dan AMC, ini bermakna bahawa kes sisi, sudut, sisi, dan oleh itu AM juga akan menjadi bisektor bâc.

Itulah sebabnya bisektor akan selalu sama dengan median dan sebaliknya.

Segmen AM membentuk sudut yang mempunyai ukuran yang sama untuk segitiga AMB dan AMC; iaitu, mereka adalah tambahan, supaya ukuran masing -masing akan:

Med. (Amb) + med. (AMC) = 180^{Sama ada}

2 _* Med. (AMC) = 180^{Sama ada}

Med. (AMC) = 180^{Sama ada} ÷ 2

Med. (AMC) = 90^{Sama ada}

Dapat diketahui bahawa sudut yang dibentuk oleh segmen AM mengenai pangkal segitiga adalah lurus, menunjukkan bahawa segmen ini benar -benar tegak lurus ke pangkalan.

Oleh itu ia mewakili ketinggian dan meditrix, mengetahui bahawa m adalah titik tengah.

Oleh itu, garisnya:

• Mewakili ketinggian SM.
• Adalah saiz sederhana.
• Ia terkandung dalam mediedtrix bc.
• Ia adalah bisektor sudut puncak â

Ketinggian relatif

Ketinggian yang relatif terhadap sisi yang sama mempunyai ukuran yang sama juga.

Boleh melayani anda: nombor sempurna: bagaimana mengenal pasti dan contohnya

Oleh kerana segitiga isosceles mempunyai dua sisi yang sama, dua ketinggian masing -masing juga akan sama.

Orocentro, Baricentro, Incentro dan Colecentro Coinsides

Seperti ketinggian, median, bisektor dan meditrix yang berkaitan dengan pangkalan diwakili pada masa yang sama oleh segmen yang sama, orthocenter, baricentro, insentre dan circumcentro akan menjadi titik colineal, iaitu, mereka akan ditemui dalam baris yang sama:

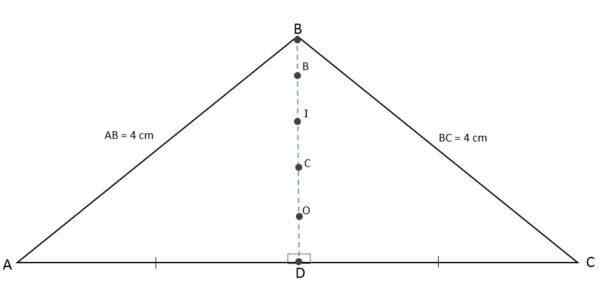Ortocenter, Baricentro, Incentro dan Circumcentro juga kebetulan

Pengiraan segitiga isosceles

Cara mengira perimeter?

Perimeter poligon dikira oleh jumlah sisi.

Seperti dalam kes ini segitiga isosceles mempunyai dua sisi dengan ukuran yang sama, perimeternya dikira dengan formula berikut:

P = 2_*(sisi a) + (sisi b).

Cara mengira ketinggian?

Ketinggian adalah garis serenjang ke pangkalan, membahagikan segitiga menjadi dua bahagian yang sama dengan memanjangkan ke puncak yang bertentangan.

Ketinggian mewakili Cateto yang bertentangan (A), separuh asas (b/2) ke Cateto bersebelahan dan bahagian "A" mewakili hipotenus.

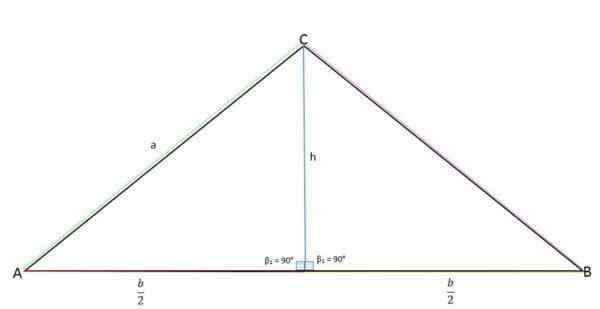Pengiraan ketinggian segitiga isosceles

Menggunakan teorem Pythagoras, nilai ketinggian dapat ditentukan:

ke² + b² = c²

Di mana:

ke² = ketinggian (h).

b² = B / 2.

c² = sisi a.

Menggantikan nilai -nilai tersebut dalam teorem Pythagoras, dan membersihkan ketinggian yang anda miliki:

h² + (b / 2)² = ke²

h² + b² / 4 = ke²

h² = ke² - b² / 4

H = √ (ke² - b² / 4).

Jika sudut yang dibentuk oleh sisi kongruen diketahui, ketinggian boleh dikira dengan formula berikut:

Cara mengira kawasan tersebut?

Segitiga sentiasa dikira dengan formula yang sama, mengalikan asas dengan ketinggian dan membahagikan dengan 2:

Terdapat kes di mana hanya ukuran dua sisi segitiga yang diketahui dan sudut yang terbentuk di antara mereka. Dalam kes ini, untuk menentukan kawasan itu perlu menerapkan alasan trigonometri:

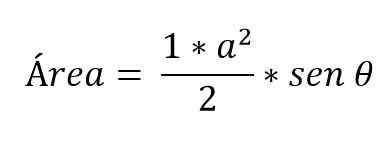
Cara mengira pangkalan segitiga?

Oleh kerana segitiga isosceles mempunyai dua sisi yang sama, untuk menentukan nilai pangkalannya, perlu mengetahui sekurang -kurangnya ukuran ketinggian atau salah satu sudutnya.

Mengetahui ketinggian, Teorem Pythagoras digunakan:

ke² + b² = c²

Di mana:

ke² = ketinggian (h).

c² = sisi a.

b² = B / 2, tidak diketahui.

Kita jelas b² dari formula dan kita perlu:

b² = a² - c²

B = √ a² - c²

Oleh kerana nilai ini sepadan dengan separuh asas, ia mesti didarab dengan 2 untuk mendapatkan ukuran lengkap asas segitiga isosceles:

B = 2 _* (√ a² - c²)

Sekiranya hanya nilai sisi yang sama dan sudut di antara mereka diketahui, trigonometri digunakan, melukis garis dari puncak ke pangkalan yang membahagikan segitiga isosceles ke dalam dua segi empat tepat segi empat tepat.

Dengan cara ini, separuh daripada pangkalan dikira dengan:

Nilai ketinggian dan sudut puncak yang menentang pangkalan juga dikenali. Dalam hal ini, dengan trigonometri asas dapat ditentukan:

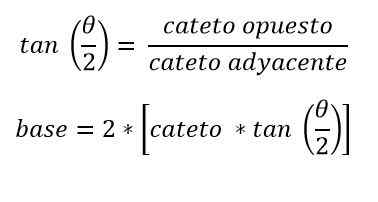
Latihan

Latihan pertama

Cari kawasan Segitiga ABC Isosceles, mengetahui bahawa dua bahagiannya mengukur 10 cm dan bahagian ketiga mengukur 12 cm.

Ia boleh melayani anda: antiderivatif: formula dan persamaan, contoh, latihan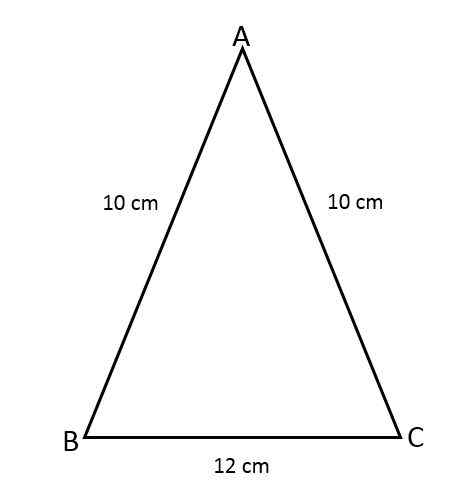

Penyelesaian

Untuk mencari kawasan segitiga, perlu.

Data segitiga isosceles berikut boleh didapati:

• Sisi yang sama (a) = 10 cm.
• Asas (b) = 12 cm.

Nilai digantikan dalam formula:

Latihan kedua

Panjang dua sisi yang sama dari segi tiga isosceles berukuran 42 cm, kesatuan sisi ini membentuk sudut 130^{Sama ada}. Tentukan nilai bahagian ketiga, kawasan segitiga dan perimeter itu.

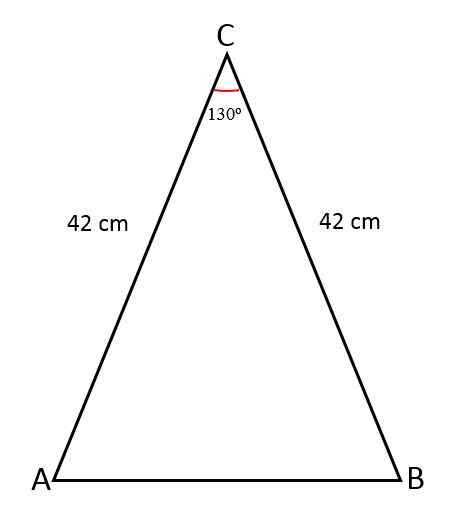
Penyelesaian

Dalam kes ini, ukuran sisi dan sudut diketahui antara ini.

Untuk mengetahui nilai bahagian yang hilang, ia.

• Sisi sama (a) = 42 cm.
• Sudut (ɵ) = 130^{Sama ada}

Sekarang, dengan trigonometri, nilai separuh asas dikira, yang sepadan dengan separuh daripada hipotenus:

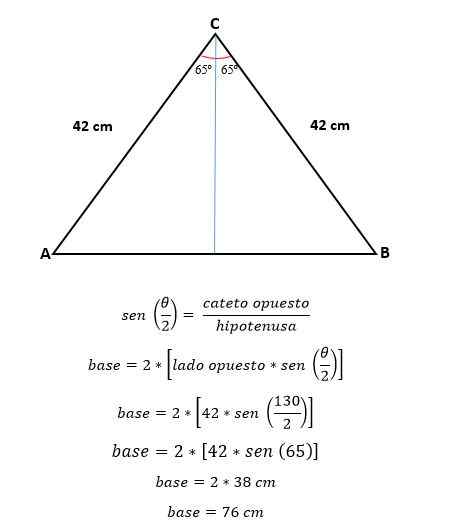
Untuk mengira kawasan itu perlu mengetahui ketinggian segitiga itu, yang boleh dikira oleh trigonometri atau oleh teorem Pythagoras, sekarang bahawa nilai pangkalan telah ditentukan.

Oleh trigonometri akan:

Perimeter dikira:

P = 2_*(sisi a) + (sisi b).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Latihan ketiga

Kirakan sudut dalaman segitiga isosceles, mengetahui bahawa sudut asas ialah â = 55^{Sama ada}

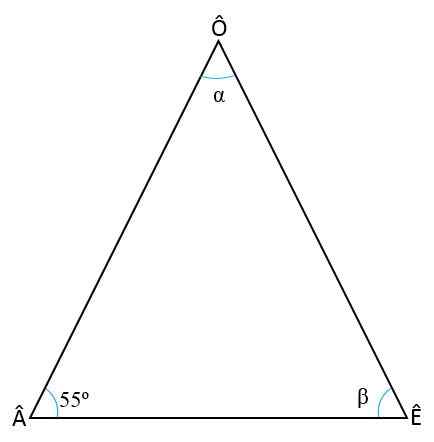
Penyelesaian

Untuk mencari kedua -dua sudut yang hilang (ê dan ô) adalah perlu untuk mengingati dua sifat segitiga:

• Jumlah sudut dalaman setiap segitiga akan selalu = 180^{Sama ada}:

 + ê + ô = 180 ^{Sama ada}

• Dalam segitiga isosceles, sudut pangkalan sentiasa kongruen, iaitu, mereka mempunyai ukuran yang sama, oleh itu:

 = ô

Ê = 55^{Sama ada}

Untuk menentukan nilai sudut ê, nilai -nilai sudut lain dalam peraturan pertama diganti dan ê dibersihkan:

55^{Sama ada} + 55^{Sama ada} + Ô = 180 ^{Sama ada}

110 ^{Sama ada} + Ô = 180 ^{Sama ada}

Ô = 180 ^{Sama ada} - 110 ^{Sama ada}

Ô = 70 ^{Sama ada}.

Rujukan

1. Álvarez, e. (2003). Unsur Geometri: Dengan banyak latihan dan geometri kompas. Universiti Medellin.
2. Álvaro rendón, ke. R. (2004). Lukisan Teknikal: Buku Nota Aktiviti.
3. Malaikat, a. R. (2007). Algebra Elementary. Pendidikan Pearson.
4. Arthur Goodman, l. H. ( Sembilan belas sembilan puluh enam). Algebra dan trigonometri dengan geometri analisis. Pendidikan Pearson.
5. Baldor, a. (1941). Algebra. Havana: Budaya.
6. José Jiménez, l. J. (2006). Matematik 2.
7. Tuma, j. (1998). Buku Panduan Matematik Kejuruteraan. Wolfram Mathworld.