Segitiga bodoh

Kami menerangkan apa segitiga bodoh, elemen, ciri, jenis, contoh dan senaman yang diselesaikan

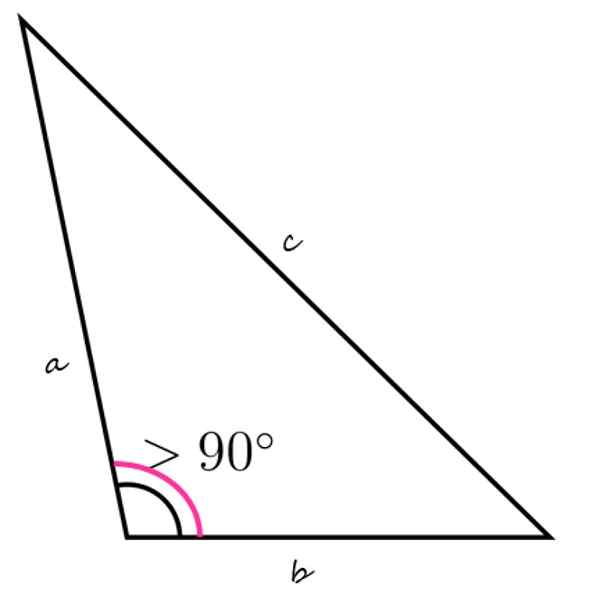Segitiga bodoh dicirikan dengan mempunyai sudut dalaman lebih besar daripada 90º

Apa itu segitiga bodoh?

A Segitiga bodoh Ia adalah angka rata, ditutup dan dengan tiga sisi, yang juga mengandungi sudut dalaman bodoh, iaitu, lebih besar daripada 90º dan kurang dari 180º.

Mana -mana segitiga mengandungi 3 sudut dalaman, dan jika salah seorang daripada mereka bodoh, dua yang lain adalah, dengan kekerasan, akut, kerana jumlah sudut dalaman mana -mana segitiga, sentiasa sama dengan 180º.

Angka atas menunjukkan contoh segitiga bodoh, dengan sudut dalaman kiri bawah lebih besar daripada 90º. Sudut dalaman yang selebihnya mesti menambah kurang daripada 90º, hanya dengan cara ini benar bahawa jumlah ketiga adalah sama dengan 180º.

Sebagai tambahan kepada segitiga bodoh, terdapat segitiga yang akut, jika semua sudut dalamannya akut, dan segi empat tepat segi empat tepat, ketika salah satu sudut dalaman mengukur tepat 90º.

Unsur -unsur segitiga bodoh

Segitiga obtusángulos mempunyai unsur -unsur yang sama untuk semua segitiga: mereka adalah angka rata 3 -sisi, dengan 3 sudut dalaman dan 3 simpul. Di samping itu, mereka mempunyai segmen yang ketara, yang dipanggil Cevians, seperti ketinggian, median dan mediatrix, dan titik di mana Cevians bersilang.

Setiap elemen ini ditakrifkan secara ringkas seperti berikut:

-Sisi, adalah segmen yang membentuk angka.

-Simpang, titik persimpangan setiap beberapa sisi bersebelahan.

-Sudut dalaman, Mereka berada di antara dua sisi bersebelahan, di bahagian dalam angka itu, bertepatan dengan puncak sudut dengan segitiga.

-Sudut luaran, Mereka berada di antara satu sisi dan lanjutan sebelah bersebelahan, di luar angka, puncaknya biasa, kedua -dua segitiga dan sudut. Jumlah ukuran antara sudut dalaman dan sudut bersebelahan luarannya adalah 180º, sehingga mereka adalah sudut pelengkap.

Ia boleh melayani anda: Ujian Tukey: Apa, dalam hal contoh, diselesaikan senaman

-Ketinggian, Ini adalah ukuran segmen tegak lurus yang bergabung dengan puncak dengan sebaliknya, atau dengan lanjutan ini.

-Median, garis yang diarahkan dari puncak ke pusat sebaliknya.

-MEDIRIX, segmen tegak lurus ke sisi dan yang melewati pusatnya.

-Bisector, Ia adalah segmen yang membahagikan setengah sudut dalaman segitiga.

-Orocentro, titik persimpangan tiga ketinggian.

-Barycenter, Juga dipanggil centroid, ia adalah titik di mana tiga median bersilang.

-Circumcentro, Di sini tiga meditrices dipotong.

-Insenter, Titik pertemuan bisektor.

Sebaik sahaja konsep -konsep ini telah dikaji semula, beberapa ciri yang paling ketara dari segitiga bodoh diterangkan di bawah.

Ciri -ciri

1.- Jumlah tiga sudut dalaman segitiga bodoh adalah 180º, oleh itu, hanya satu sudut dalamannya boleh lebih besar daripada 90º, manakala jumlah baki dua adalah kurang daripada 90º.

2.- Bahagian terpanjang segitiga bodoh bertentangan dengan sudut bodoh.

3.- Dalam segitiga bodoh, ketinggian dari simpang yang membuat sudut akut, menyeberangi sambungan sisi bertentangan.

4.- Orthocenter segitiga bodoh keluar dari angka.

5.- Circumcentro segitiga bodoh juga jatuh dari segitiga (ini tidak berlaku dengan segitiga acutangle).

6.- Hanya mungkin untuk mendaftarkan persegi di segitiga bodoh, menyokong salah satu sisi persegi di sisi terpanjang segitiga. Dua dataran boleh ditarik, menyokong sisi di sisi terpendek segitiga, meninggalkan puncak tidak didaftarkan (yang tidak menyentuh sisi segitiga).

Boleh melayani anda: Tidecágono

7.- Jadilah segitiga yang bodoh (a, b, c), yang paling lama. Ketidaksamaan berikut adalah sah:

ke²+b² < c²

8.- Mereka adalah dua segitiga bodoh, yang masing -masing adalah (A, B, C) dan (U, V, W). Sisi terpanjang masing -masing adalah C dan W, jadi ketidaksamaan berikut dipenuhi:

A ∙ u + b ∙ v < c∙w

Jenis segitiga yang menghalang

Segitiga bodoh boleh terdiri daripada dua jenis, mengikut panjang sisi mereka:

• Isosceles
• Scalene

Mereka diterangkan secara ringkas di bawah:

Segitiga Isosceles

Ia adalah satu yang mempunyai dua sisi yang sama dan yang berbeza, iaitu, sisinya (a, a, c).

Apabila segitiga isosceles kedua -duanya bodoh, sisi ukuran "a" lebih pendek dan bahagian "c" adalah yang paling lama. Sudut bodoh terbentuk di antara sisi yang sama, manakala kedua -dua sudut akut adalah ukuran yang sama dan terbentuk di antara sisi "a" dan sisi "c".

Dan seperti yang dinyatakan di bahagian sebelumnya, sisi "C", kerana ia adalah yang paling lama, ia menentang sudut bodoh.

Segitiga Scalene

Tiga sisi segitiga scalene mempunyai ukuran yang berbeza: (a, b, c).

Contoh

Contoh 1

Segitiga yang ditunjukkan dalam angka berikut adalah bodoh. Sudut bodoh ialah γ = 114.Ke -5 dan disahkan bahawa jumlah tiga sudut dalaman adalah 180º:

114.5 + 36.8º + 28.6th ≈ 180º

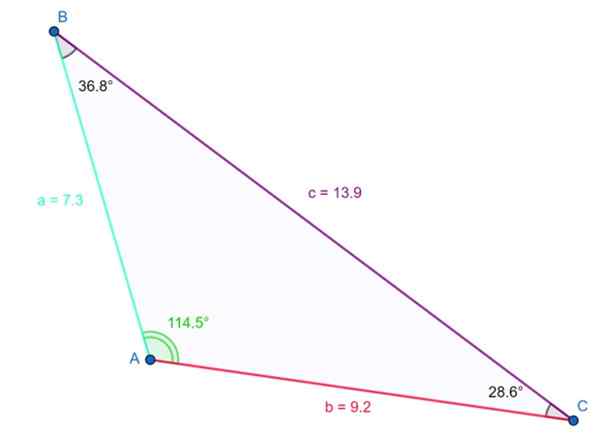Contoh segitiga bodoh. Sumber: f. Zapata

Bahagian terpanjang mengukur 13.9 unit dan menentang sudut bodoh. Ketidaksamaan yang disebutkan di atas juga dipenuhi:

ke²+b² < c²

Boleh melayani anda: Hubungan perkadaran: konsep, contoh dan latihan

Ya A = 7.3 dan B = 9.2, kemudian:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Contoh 2

Di segitiga Calabi, adalah mungkin untuk meletakkan persegi yang terbesar, dalam tiga cara yang berbeza dalam segitiga, seperti yang ditunjukkan dalam angka berikut.

Segitiga Calabi adalah isosceles dan bodoh. Sudut bodoh adalah kira -kira 101.736 ° dan sudut akut pada ukuran asas kedua -dua 39.Ke -13, juga kira -kira.

Latihan diselesaikan

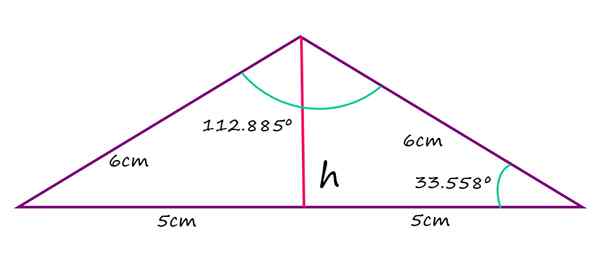
Sisi yang sama dari segi triangle isosceles ukur 6 cm, manakala bahagian terpanjang mengukur 10 cm. Kirakan nilai sudut bodoh, iaitu sudut agudos yang tinggal dan ketinggian dari puncak tersebut ke pangkalan.

Penyelesaian

Teorem Cosine boleh digunakan untuk mencari kosinus sudut bodoh. Kemudian, dengan bantuan kalkulator sudut yang dipersoalkan ditentukan, dilambangkan sebagai γ.

Teorem Coseno menyatakan bahawa:

c² = a² +b² - 2ab ∙ cos γ

Di mana γ adalah sudut antara sisi a dan b. Oleh kerana segitiga adalah isosceles, sisi a dan b adalah sama, oleh itu:

c² = 2a² - ke -2²∙ cos γ

Membersihkan cos γ:

 Sudut bodoh adalah arka kosinus -0.38889, yang kira -kira 112.885º. Nilai α, sudut akut yang dibentuk oleh sisi 6 cm dengan 10 cm ialah:

2α + 112.885º = 180º

α = (180 - 112.885)/2 = 33.558º

Isosceles segitiga. Sumber: f. Zapata

Bagi ketinggian segitiga, diukur dari pangkalan, ia diperoleh dengan memerhatikan bahawa ketinggian ini membahagikan segitiga menjadi dua segi empat tepat yang sama, dengan hypotenusa sama dengan 6 cm dan asas 5 cm. Dalam kes sedemikian, teorem Pythagoras terpakai untuk mencari nilai h: