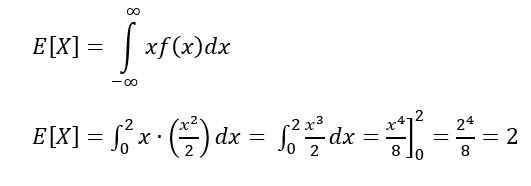Pemboleh ubah rawak berterusan

Kami menerangkan pembolehubah rawak yang berterusan, ciri -ciri, contoh dan senaman yang diselesaikan

Apakah pemboleh ubah rawak yang berterusan?

A Pemboleh ubah rawak berterusan Ia adalah nilai berangka yang diperoleh secara rawak, yang hasil daripada melakukan eksperimen dan boleh mengambil nilai tak terhingga. Ini bermakna, diketahui dua nilai berturut -turut pembolehubah, selalu mungkin untuk mencari nilai perantaraan yang lain di antara mereka.

Dengan mempunyai jumlah nilai yang tidak terhingga, pengumpulan nilai pembolehubah berterusan tidak perakaunan dan hampir selalu tergolong dalam set nombor nyata.

Contoh pembolehubah jenis ini adalah kedudukan, berat dan suhu badan seseorang, tetapi tidak banyaknya dapat ditakrifkan, beberapa contoh akan didapati di bawah. Berbeza dengan pemboleh ubah rawak yang berterusan, terdapat pemboleh ubah rawak yang bijak, yang perakaunan, seperti bilangan anak perempuan dalam keluarga, atau berapa banyak kereta yang dijual oleh agensi selepas satu bulan.

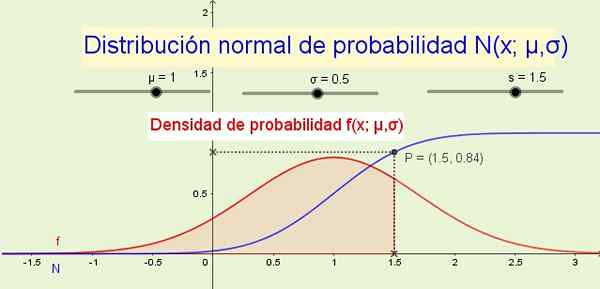
Pembolehubah rawak diskret kerap mengikuti taburan kebarangkalian biasa. Sumber: f. Zapata.

Pemboleh ubah rawak yang berterusan dilambangkan dengan cara huruf besar seperti x, dan nilai tak terhingga yang dibeli adalah hasil yang mungkin dari eksperimen rawak:

X = x₁, x₂, x₃,... ∞

Setiap nilai mempunyai kebarangkalian kejadian tertentu, dan model yang mana kebarangkalian ini dikira, ia dipanggil taburan kebarangkalian.

Tetapi, kerana x mengambil nilai tak terhingga, kebarangkalian untuk nilai tertentu pembolehubah tidak dapat dikira. Oleh itu, adalah perlu untuk menentukan fungsi f (x), yang dipanggil fungsi pengedaran terkumpul, atau hanya fungsi pengedaran, mengikut kebarangkalian terkumpul dikira kepada nilai tertentu atau antara dua nilai:

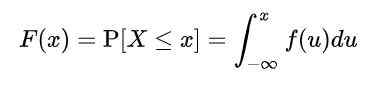
Di mana f (u) terima nama fungsi ketumpatan. Ditakrifkan dengan cara ini, F (x) mewakili kebarangkalian bahawa X antara -∞ dan x.

Ciri -ciri pemboleh ubah rawak yang berterusan

Pembolehubah rawak berterusan selesai f (x).

Fungsi ketumpatan f (x) Mesti memenuhi sifat berikut:

• Fungsinya f (x) Ia positif: f (x)> = 0
• Kawasan di bawah lengkung y = f (x) Selalunya sama dengan 1, iaitu kebarangkalian berlakunya keputusan x Dalam selang (-∞, +∞) adalah 100%.
• Kebarangkalian bahawa x berada dalam selang [a, b] dikira oleh integral yang ditakrifkan berikut:

Boleh melayani anda: curtosis: definisi, jenis, formula, apa itu, contohnya

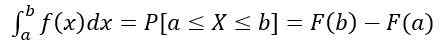
Yang bersamaan dengan kawasan di bawah lengkung y = f (x), difahami antara ke dan b. Selain:

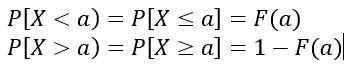
Nilai -nilai f (x) Mereka tidak mewakili kebarangkalian, jadi P [x = c] = 0. Nilai yang berkaitan adalah yang sepadan dengan kawasan di bawah lengkung y = f (x), yang mewakili kebarangkalian.

• Dengan mendapatkan fungsi pengedaran F (x) berkenaan dengan x, diperolehi f (x).

Graf f (x) Untuk pemboleh ubah rawak yang berterusan, ia sama dengan poligon kekerapan yang dibina untuk pemboleh ubah statistik diskret, dengan perbezaan yang, untuk pemboleh ubah rawak, lebar selang menjadi infinitesimal.

Harapan

Harapan adalah salah satu langkah ciri pemboleh ubah yang berterusan. Harapan atau nilai yang diharapkan X Menunjukkan nilai yang dijangka berlaku lebih kerap, dan dikira melalui integral berikut:

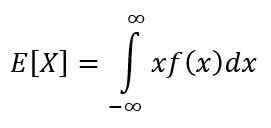
Sifatnya adalah:

• E [a∙ x] = a∙ e [x]
• E [x + y] = e [x] + e [y]]
• E [a∙ x+b∙ y] = a∙ e [x] + b∙ e [y]

Di mana jumlahnya ke dan b Mereka adalah nombor sebenar.

Contoh

Seperti yang dinyatakan sebelum ini, terdapat banyak situasi di mana satu atau lebih pembolehubah rawak berterusan dapat ditakrifkan. Dalam bidang sains dan lain -lain, yang paling biasa adalah masa, panjang, berat, kelantangan dan suhu:

Masa

Untuk mengoptimumkan proses dan perkhidmatan, eksperimen direka untuk mengkaji masa yang mereka ambil untuk dijalankan:

X = masa yang membawa pelanggan ke tetingkap bank.

Y = apa yang memerlukan tempat makanan segera dalam melayani pesanan.

Z = masa di mana tindak balas kimia tertentu berlaku.

Statur dan berat

Dalam banyak kajian mengenai orang dan haiwan, statur dan berat adalah relevan:

X = Ketinggian kanak -kanak perempuan dalam kursus ke -6. Ijazah di setiap sekolah di bandar.

Boleh melayani anda: Congruence: angka kongruen, kriteria, contoh, latihan

Y = berat bayi semasa lahir di hospital awam.

Z = berat lembu di ladang.

Suhu

Suhu adalah parameter yang relevan dalam pelbagai proses kimia, yang biasanya mengambil nilai tak terhingga dalam julat tertentu:

X = suhu di mana tindak balas kimia tertentu berlaku, mengetahui bahawa ini berlaku antara 80 ºC dan 120 ºC.

Latihan yang diselesaikan

Latihan 1

Tentukan apakah pembolehubah rawak yang berterusan:

1. Bilangan pelajar yang menghadiri kopi universiti hingga ke hari.
2. Tekanan darah pesakit yang datang ke bilik kecemasan.
3. Panjang sayap burung, spesies terancam, yang mendiami rizab.
4. Masa antara satu orang dan yang lain dirawat di bank.
5. Jumlah produk yang cacat sebulan di kilang.
6. Tahap kolesterol di dalam ayam ladang.
7. Jumlah lampu jalan di jalan, sebanyak 12.

Penyelesaian

1.- Bilangan pelajar yang dihadiri hari ini adalah kebas, oleh itu, pembolehubah ini tidak berterusan, tetapi bijak.

2.- Ia berterusan. Tekanan darah pesakit boleh mengambil nilai dalam julat tertentu.

3.- Pemboleh ubah berterusan, kerana panjang sayap burung mengambil nilai antara minimum dan maksimum, bergantung kepada spesies.

4.- Masa antara perkhidmatan pelanggan berubah -ubah dan boleh mengambil nilai dalam julat tertentu, contohnya, antara 1 dan 5 minit.

5.- Oleh kerana bilangan produk yang rosak adalah perakaunan, ia adalah pemboleh ubah rawak yang bijak.

6.- Pembolehubah ini berterusan, kerana tahap kolesterol dalam ayam mengambil nilai dalam julat yang ditentukan sebelumnya.

Boleh melayani anda: sudut pelengkap: yang mana dan bagaimana ia dikira, contoh, latihan

7.- Berhati -hati. Bilangan lampu pencahayaan yang berfungsi adalah jumlah perakaunan.

Latihan 2

Pemboleh ubah rawak berterusan ditakrifkan X = "Tahap Kolesterol " Dalam pelbagai jenis ayam ladang, yang mempunyai fungsi ketumpatan berikut f (x):

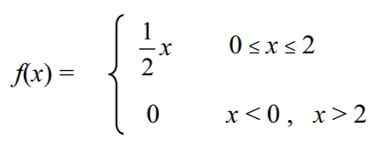
Kirakan perkara berikut:

1. F (x)
2. P [x ≤2]
3. Harapan Ex]

Penyelesaian kepada

Menurut definisi yang diberikan pada mulanya:

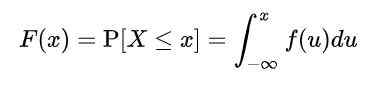
Oleh itu, F (x) Ia adalah fungsi di bahagian. Untuk selang waktu x<0, F (x) Ia sama dengan 0, kerana sifat -sifat yang dinyatakan pada mulanya.

Dalam selang waktu 0≤x≤2, Integral tidak terbatas diselesaikan:

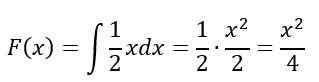
Akhirnya, untuk selang waktu x> 2, F (x) = 1, Oleh itu, menurut Properties, F (x) Ia tetap seperti ini:

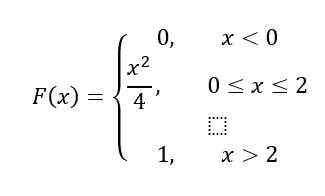
Penyelesaian b

Kebarangkalian yang dicari adalah F (1.2) dan como x = 1.2 Ia dijumpai antara 0≤x≤2, bahagian itu F (x) Untuk menilai:

F (1.2) = ¼ ∙ (1.2)² = 0.36.

Penyelesaian c

Untuk mengira harapan atau nilai yang diharapkan, ia digunakan: