Ujian hipotesis

Apakah ujian hipotesis?

The ujian hipotesis, Dalam statistik, ini adalah prosedur yang digunakan untuk memeriksa bagaimana berjaya adalah sangkaan mengenai a penduduk. Ramalan ini dipanggil hipotesis, pada dasarnya mereka diambil sebagai benar, sehingga beberapa bukti mengesahkan atau menafikannya.

Bukti ini dibekalkan oleh data sampel, yang berasal dari sebahagian besar penduduk, yang dipanggil Contoh. Teori kebarangkalian menyediakan teknik yang diperlukan untuk membezakan kebenaran hipotesis.

Contoh hipotesis adalah:

-Purata suhu badan manusia ialah 36.1 ºC.

-Rata -rata, beg kacang asin yang dihasilkan di kilang makanan ringan berat 50 g.

-80% penduduk bandar, membuat pembelian dalam talian dalam tempoh 6 bulan yang lalu.

-Skor ujian IQ untuk pelajar universiti dari institusi yang terkenal, mempunyai sisihan piawai 15.

-Pembolehubah rawak tertentu x mengikuti taburan Poisson.

Empat pertama adalah jenis hipotesis parametrik, Kerana ini adalah pernyataan mengenai beberapa parameter penduduk, seperti purata, sisihan piawai atau beberapa perkadaran.

Sebaliknya, hipotesis terakhir menetapkan pengedaran pemboleh ubah rawak, dan kerana ia tidak merujuk kepada mana -mana parameter atau harta penduduk, dikatakan bahawa ia adalah hipotesis bukan parametrik.

Hipotesis nol dan hipotesis alternatif

Terdapat dua jenis hipotesis yang akan melakukan ujian, yang akan membezakannya:

-Hipotesis nol, dilambangkan sebagai h₀, menyatakan bahawa parameter di bawah kajian mempunyai nilai yang ditetapkan, atau pemboleh ubah rawak mengikuti taburan tertentu. Oleh itu, secara simbolik menyatakan hipotesis nol, simbol kesamaan selalu digunakan.

-Hipotesis alternatif: dipanggil h₁, Beliau menegaskan bahawa parameter atau pengedaran adalah berbeza dari apa hipotesis nol memastikan, oleh itu, secara simbolik menyatakan hipotesis alternatif, simbol digunakan: atau ≠, tetapi tidak pernah kesamaan.

Ia boleh melayani anda: harta algebra kunci: demonstrasi, contoh

Apabila hipotesis nol diterima, hipotesis alternatif ditolak, sehingga kedua -duanya saling eksklusif.

Tahap kepentingan

Ini adalah ukuran untuk kesilapan yang boleh dibuat semasa melakukan ujian hipotesis. Ia ditakrifkan sebagai kebarangkalian menolak hipotesis nol, kerana itu benar. Ia biasanya dilambangkan dengan huruf Yunani α:

α = p (menolak h₀ Bila benar)

Nilai yang biasa digunakan untuk α adalah 0.01, 0.05, dan 0.10; Menjadi yang kedua adalah penggunaan yang paling kerap. Bersama masing -masing kepada 1%, 5% dan 10% kebarangkalian membuat kesilapan apabila menolak h₀, Tetapi dalam apa jua keadaan, semakin rendah tahap kepentingan, hasil ujian yang lebih dipercayai.

Nilai alfa (α) dapat difahami sebagai pecahan peratusan ekor kanan (atau kiri), dalam pengedaran normal yang ditandakan (μ = 0 dan σ = 1) dan nilai -nilai ini selalu berlaku pada z = 2.33 untuk α = 0.01; pada z = 1.65 untuk α = 1.65 dan pada z = 1.29 untuk α = 0.1.

Langkah -langkah untuk melakukan ujian hipotesis

Langkah 1

Tentukan masing -masing hipotesis null dan alternatif. Hipotesis nol menetapkan bahawa parameter yang sedang dikaji, yang dipanggil θ, sama dengan nilai rujukan, dilambangkan sebagai θ₀:

H₀: θ = θ₀

Sebagai contoh, jika kesan ubat diselidiki pada ciri tertentu populasi tikus makmal, hipotesis nol merenungkan bahawa ubat ini tidak membuat perbezaan dalam ciri -ciri sedemikian dan ini mempunyai nilai malar θ₀.

Untuk melambangkan hipotesis nol, tanda kesamaan selalu digunakan, sebaliknya, hipotesis alternatif menggunakan salah satu simbol atau ≠.

Dalam contoh ubat, hipotesis alternatif menegaskan bahawa sebatian itu mempunyai kesan ke atas ciri -ciri yang dipersoalkan. Oleh itu, ini lebih besar, lebih rendah, atau hanya berbeza dari nilai rujukan θ₀.

Boleh melayani anda: notasi faktorial: konsep, contoh dan latihan

Langkah 2

Pilih tahap kepentingan yang sesuai, yang biasanya ditubuhkan pada 5 %, seperti yang dinyatakan sebelum ini.

Langkah 3

Tentukan populasi dan ekstrak daripadanya sampel, atau sampel, yang analisisnya akan membezakan hipotesis dan menentukan penerimaan atau penolakan hipotesis nol.

Langkah 4

Pilih dan hitung nilai statistik percubaan untuk data yang dikumpulkan, dari mana bukti yang diperlukan diperolehi untuk membuat keputusan untuk menerima atau menolak hipotesis nol. Pilihan statistik percubaan bergantung pada parameter yang dipilih: min, sisihan, perkadaran atau lain -lain.

Statistik percubaan diperoleh dengan menukar parameter sampel ke dalam skor Z, pelajar, R Pearson atau Statistik Square Chi, menurut reka bentuk eksperimen yang dipilih. Ada formula untuk ini.

Biasanya, jika parameter populasi adalah purata μ, "X bar" adalah sampel min, sisihan piawai σ diketahui dan saiz sampel adalah n> 30, statistik ujian z_C Ia dikira dengan skor Z:

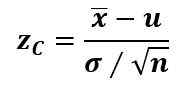
Dan ketika n < 30, pero σ es desconocida, se usa la t de Student.

Langkah 5

Menetapkan kriteria untuk penerimaan atau penolakan hipotesis nol, yang boleh dilakukan melalui dua prosedur:

• Melalui nilai p.
• Dengan perbandingan dengan nilai kritikal.

Nilai p bersamaan dengan kebarangkalian mendapatkan hasil yang dijumpai, kerana hipotesis nol adalah benar. Sekiranya nilai -nilai ini kecil, hipotesis nol ditolak, jika tidak, ia diterima. Walau apa pun, nilai p tidak membuktikan bahawa hipotesis alternatif adalah benar.

Perlu dipertimbangkan bahawa dalam ujian hipotesis adalah mungkin untuk membuat dua jenis kesilapan:

• Taipkan kesilapan: Menolak h₀ Bila benar. Kebarangkaliannya adalah α dan bersamaan dengan tahap kepentingan bukti.
• Ralat Jenis II: Terima h₀ Apabila ia sebenarnya palsu. Kebarangkaliannya dilambangkan sebagai β.

Ia dapat melayani anda: apakah hubungan antara kawasan rhombus dan segi empat tepat?

Langkah 6

Buat keputusan untuk menerima atau menolak hipotesis nol. Sekiranya nilai p digunakan, apabila p < α, se rechaza H₀ Dan H diterima₁, Dan jika tidak, h diterima₀. Set nilai p < α se conoce como rantau kritikal. Sekiranya statistik dalam selang ini, h ditolak₀.

Begitu juga, nilai kritikal dipilih, menurut parameter populasi yang dipilih. Jika ini adalah purata, teruskan seperti berikut:

• Ujian ekor: θ < θ₀ atau θ> θ₀
• Ujian dua ekor: | θ | < θ₀

Contoh yang diselesaikan

Mesin mengeluarkan skru yang nilai nominalnya mestilah panjang 800 milimeter, dengan sisihan piawai sebanyak 5%.

Sampel rawak diambil, iaitu, pada hari -hari yang berlainan minggu pengeluaran, yang berjumlah kira -kira 40 skru. Apabila panjang purata sampel dikira, nilai 790 milimeter diperolehi.

Tentukan sama ada panjang purata adalah toleransi dengan tahap kepentingan masing -masing sebanyak 1%, 5% dan 10%.

Penyelesaian

Yang pertama adalah untuk mengira statistik ujian purata, yang dalam kes ini adalah sisihan purata dibahagikan antara kesilapan populasi standard:

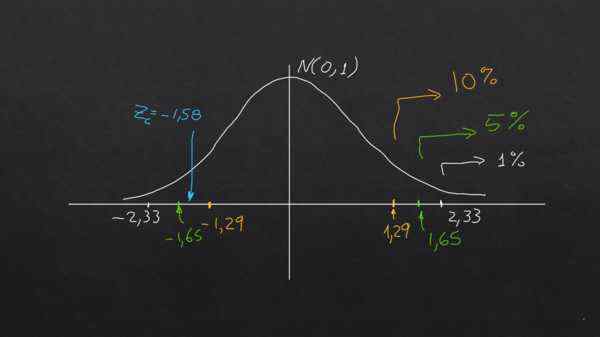
Zc = (790 - 800) / (40 / √40) = -1,58

Di mana ia telah diambil kira bahawa sisihan piawai 5% sepadan dengan 40 dari 800.

Hipotesis nol adalah bahawa sampel purata berada dalam toleransi yang dibenarkan untuk tahap kepentingan yang diperlukan, dengan syarat bahawa | ZC | kurang daripada nilai yang ditandatangani | zt |, jika tidak hipotesis nol ditolak.

Untuk kepentingan 1% dan 5%, hipotesis nol dipenuhi, kerana | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

Walau bagaimanapun, untuk kepentingan 10% ia berlaku bahawa | zc | > 1.29. Iaitu, pada tahap kepentingan ini hipotesis nol tidak dipenuhi.

Grafik berikut menjelaskan kesimpulan:

Grafik ditunjukkan sebagai bergantung pada tahap kepentingan memerlukan hipotesis yang sama dapat diterima atau ditolak dengan data yang sama. Sumber: f. Zapata.