Anggaran mengikut selang waktu

Berapakah anggaran selang waktu?

The Anggaran mengikut selang waktu Ini adalah cara untuk menentukan julat nilai di mana purata populasi boleh dimasukkan, berdasarkan maklumat sampel saiz terhingga, secara rawak diekstrak dari jumlah penduduk.

Dia Selang anggaran Ia lebih rendah kerana sampel lebih besar, tetapi menjadi lebih luas jika tahap atau peratusan kebolehpercayaan kenaikan yang sama.

Sekiranya anda ingin mengetahui purata populasi pembolehubah tertentu dalam bentuk yang tepat, maka jumlah penduduk harus dipertimbangkan, sesuatu yang tidak selalu dapat dilaksanakan, karena jika ia adalah penduduk yang sangat besar, ia adalah mahal untuk mendapatkan data dari seluruh penduduk. Atas sebab ini, satu atau lebih sampel rawak dari jumlah penduduk digunakan untuk diambil.

Ia berdasarkan hipotesis bahawa, dengan mengekstrak sampel rawak, tidak berat sebelah dan mengambil kira secara proporsional semua strata, maka nilai purata sampel harus sangat dekat dengan purata penduduk.

Logik menunjukkan bahawa semakin besar data sampel, perbezaan antara nilai sampel purata dan nilai populasi purata lebih rendah.

Selang anggaran

Dalam praktiknya, melainkan jika penduduk yang lengkap diketahui, hanya mungkin untuk mencari, dengan kebarangkalian, selang di mana penduduknya dapat dijumpai, berdasarkan sampel saiz terhingga.

Dalam kes penduduk yang mengikuti taburan normal, dengan Sisihan piawai σ , The Perbezaan standard Antara purata penduduk μ dan purata sampel saiz n diberikan oleh:

| μ - | ≤ σ / √n

Di sini, perkataan "standard" menunjukkan bahawa 68% sampel saiz n, Mereka mempunyai nilai purata antara selang waktu [μ - σ / √n, μ + σ / √n].

Boleh melayani anda: kriteria pembahagian: apakah mereka, apakah kegunaan dan peraturan

Anggaran standard

Tafsiran alternatif di atas adalah untuk mengatakan bahawa populasi bermaksud diperoleh dari sampel saiz n dan nilai purata difahami dalam selang waktu  [ - σ / √n, + σ / √n], Dengan kebarangkalian 68%.

Dalam kes -kes yang paling nyata, tidak mungkin untuk mengetahui sisihan penduduk yang standard, jadi σ Ia dianggarkan oleh sisihan piawai sampel s, yang dikira seperti berikut:

S = √ (Σ (x_Yo - )² / √ (n-1).

Dari situ anda mendapat selang yang boleh mengandungi penduduk min dengan tahap keyakinan 68% (tahap keyakinan standard), yang diberikan oleh:

  -s / √n ≤ μ ≤ + s / √n

Selang pengukuran penduduk ini dikenali sebagai selang anggaran standard dan hanya diperoleh dengan data yang tersedia n.

Dari formula sebelumnya, ia mengikutinya, jika anda ingin mengukuhkan selang anggaran pada separuh, ia perlu Quadruple Saiz sampel.

Anggaran dengan selang keyakinan

Dalam kajian tertentu, tahap standard 68% tidak mencukupi, maka perlu untuk menentukan selang waktu dengan tahap keyakinan sewenang -wenang γ.

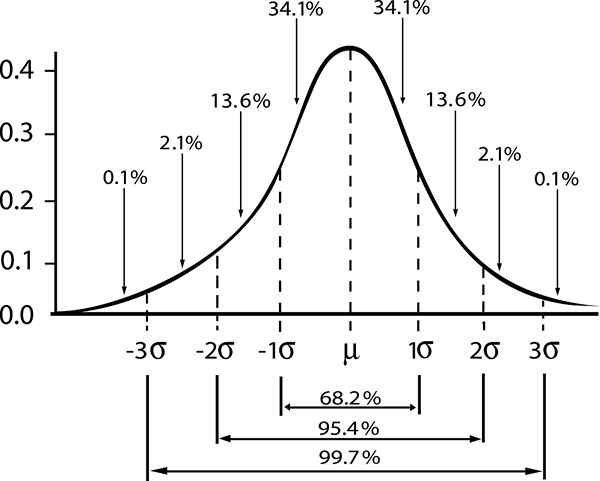
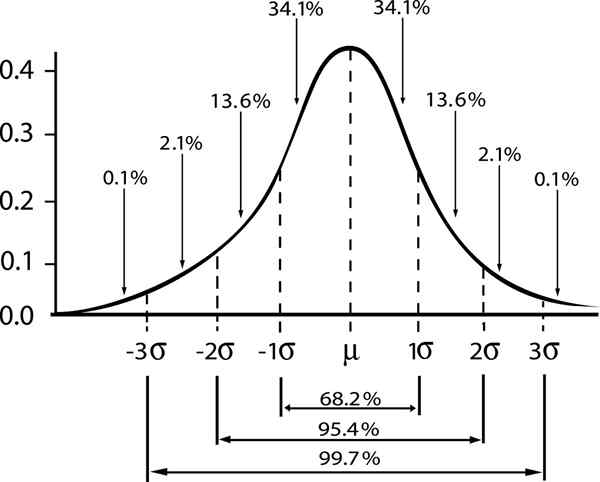Hubungan antara margin kebolehpercayaan dan selang dalam taburan Gaussian ditunjukkan

Sekiranya kita menunjukkan ε Ralat standard s/√n, Kemudian ralat anggaran untuk tahap keyakinan γ akan diberikan oleh:

E = Zγ⋅ε.

Di mana Zγ Ia adalah bilangan yang mana ralat standard didarabkan, dan dengan itu memperoleh margin kesilapan dengan tahap keyakinan sewenang -wenang γ.

Untuk mendapatkan faktor Zγ, teruskan seperti berikut:

Ia boleh melayani anda: Nombor rasional: sifat, contoh dan operasi

Langkah 1

Adalah panggilan tahap kepentingan α sepadan dengan tahap kepercayaan γ oleh formula berikut:

α = 1 - γ

Langkah 2

Nilai ditentukan:

Ini adalah kekerapan terkumpul dalam taburan normal yang dinyatakan N (0.1) Dalam selang (-∞, Zγ ].

Langkah 3

Ia membersihkan Zγ Persamaan:

N (zγ) = 1 - α/2

Oleh kerana ia adalah persamaan yang penting, pelepasan ini diperoleh dari jadual pengedaran normal, menggunakan kaedah interpolasi linear.

Langkah 4

Sebagai alternatif kepada penggunaan jadual, fungsi statistik yang dimasukkan dalam spreadsheet seperti Excel, Sama ada Lembaran Google. Program -program ini menggabungkan fungsi songsang biasa N^-1, Jadi faktor pembetulan Zγ Ia diperoleh secara langsung menilai fungsi songsang ini:

Zγ = n^-1(1 - α/2).

Selang amanah tipikal

Tahap keyakinan yang paling kerap digunakan ialah:

• Zγ = 1; tahap keyakinan standard γ = 0.68.
• Zγ = 2; tahap keyakinan γ = 0.95 (atau tahap kepentingan 5%).
• Zγ = 3; tahap keyakinan γ = 0.997 (atau tahap 0.3%kepentingan)

Contoh

Contoh 1

Tentukan purata selang berat bayi yang baru lahir pada bulan Ogos di sebuah bandar besar berdasarkan sampel rawak 100 bayi, di mana berat purata 3100 gram diperolehi dengan sisihan standard sampel s = 1500 gram.

Penyelesaian

Pertama, kesilapan standard sampel ditentukan:

ε = s/√n = (1500 g)/√100 = 150 g.

Oleh itu, bermula dari sampel ini, dapat disimpulkan bahawa berat purata bayi yang dilahirkan pada bulan Ogos di kota itu adalah antara 2950 g dan 3250 g, dengan kebarangkalian 68%.

Contoh 2

Katakan saiz sampel bayi yang dilahirkan pada bulan yang sama bulan Ogos dan di bandar yang sama Contoh 1. Berat sampel purata ialah 3100 g dengan penyebaran standard 1500 g. 

Ia dapat melayani anda: penguraian nombor semula jadi (contoh dan latihan)

Diminta untuk menganggarkan selang berat purata bayi baru lahir di bandar itu, dari sampel baru ini.

Penyelesaian

Sekarang ralat standard berkurangan dalam faktor 1/√2, Oleh itu, ralat standard baru berat purata akan menjadi 106 g.

Kemudian ia boleh dianggarkan, dari sampel baru ini, berat purata bayi baru lahir terdiri daripada julat 2994 g hingga 3206 g, dengan kebarangkalian 68%.

Latihan

Latihan 1

Tentukan purata berat badan bayi yang baru lahir pada bulan Ogos, bermula dari sampel yang dinyatakan dalam Contoh 1, dengan kebarangkalian 95%.

Penyelesaian

Tahap kebolehpercayaan 95% menggandakan julat berat purata, berbanding tahap kebolehpercayaan 68%.

Oleh itu, purata berat bayi yang baru lahir dimasukkan dalam julat 2800 gram pada 3400 gram dengan kepastian 95%.

Latihan 2

Anggarkan dengan tahap keyakinan 99.7% selang di mana berat purata bayi baru lahir dari bandar besar akan dijumpai, jika sampel tersedia dengan berat purata 100 bayi bersamaan dengan 3100 g, dan dengan sisihan sampel standard s = 1500 g.

Penyelesaian

Margin ralat berat purata, dengan 99.7% kepastian, akan menjadi tiga kali ganda kesilapan purata, iaitu:

3*1500/√100.

Kemudian disimpulkan, dari sampel ini, bahawa berat purata bayi baru lahir akan dimasukkan dalam selang: 2650 gram hingga 3550 gram, dengan tahap pasti 99.7%. 

Dari hasil ini, ia diperhatikan seperti tahap kepastian yang lebih tinggi meningkatkan ketidakpastian berat purata ke selang jauh lebih luas.