Kesalahan peratusan
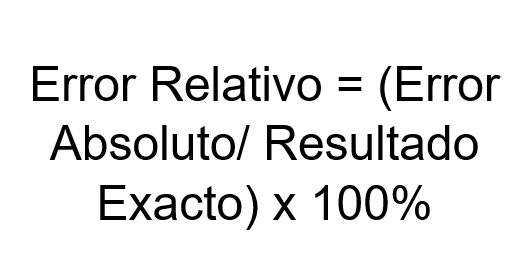
- 3566
- 309
- Ms. Edgar Carroll
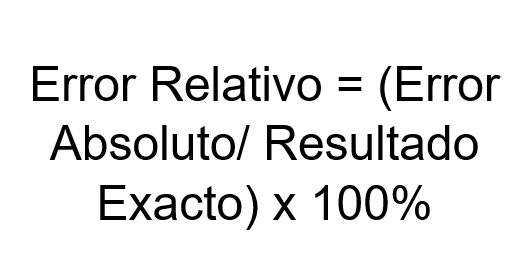
Apakah ralat peratusan?
Dia Kesalahan peratusan Ini adalah manifestasi kesilapan relatif dalam istilah peratusan. Dalam erti kata lain, ia adalah ralat berangka yang dinyatakan oleh nilai yang memberikan ralat relatif, kemudiannya didarabkan dengan 100.
Untuk memahami apa ralat peratusan, anda mesti terlebih dahulu memahami apa ralat berangka, ralat mutlak dan ralat relatif, kerana ralat peratusan diperoleh dari kedua -dua istilah ini.
Kesalahan berangka adalah salah satu yang muncul apabila ukuran diambil secara bersamaan apabila menggunakan peranti (pengukuran langsung), atau apabila formula matematik (ukuran tidak langsung) diterapkan dengan teruk.
Semua kesilapan berangka boleh dinyatakan dengan tepat atau peratusan. Bagi pihaknya, kesilapan mutlak adalah salah satu yang berlaku ketika melakukan pendekatan untuk mewakili jumlah matematik yang terhasil daripada pengukuran elemen atau aplikasi yang salah dari formula.
Dengan cara ini, nilai matematik yang tepat diubah oleh pendekatan. Pengiraan ralat mutlak dilakukan dengan menolak pendekatan kepada nilai matematik yang tepat, seperti ini:
Ralat mutlak = hasil yang tepat - Pendekatan
Unit ukuran yang digunakan untuk menunjukkan ralat relatif adalah sama yang digunakan untuk bercakap mengenai ralat berangka. Begitu juga, kesilapan ini dapat memberikan nilai positif atau negatif.
Ralat relatif adalah kuota yang diperoleh dengan membahagikan ralat mutlak dengan nilai matematik yang tepat.
Dengan cara ini, kesilapan peratusan adalah apa yang diperoleh dengan mengalikan hasil kesilapan relatif bagi setiap 100. Dengan kata lain, ralat peratusan adalah peratusan (%) ungkapan ralat relatif.
Boleh melayani anda: x kuadratRalat relatif = (ralat mutlak/ hasil tepat)
Nilai peratusan yang boleh negatif atau positif, iaitu, ia boleh menjadi nilai yang diwakili oleh kelebihan atau lalai. Nilai ini, tidak seperti kesilapan mutlak, tidak hadir unit melebihi peratusan (%).
Ralat relatif = (ralat mutlak/ hasil tepat) x 100%
Misi kesilapan relatif dan peratusan adalah untuk menunjukkan kualiti sesuatu, atau memberikan nilai perbandingan.
Contoh pengiraan ralat peratusan
1. Pengukuran dua tanah
Dengan mengukur dua lot atau tanah, dikatakan bahawa terdapat kira -kira 1 m kesilapan dalam pengukuran. Tanah adalah 300 meter dan satu lagi dari 2.000.
Dalam kes ini, kesilapan relatif pengukuran pertama akan lebih besar daripada yang kedua, kerana dalam perkadaran 1 m mewakili peratusan yang lebih tinggi.
300 m banyak:
EP = (1/300) x 100%
EP = 0.33%
Banyak 2.000 m:
EP = (1/2.000) x 100%
EP = 0.05%
2. Pengukuran aluminium
Di makmal blok aluminium dihantar. Apabila mengukur dimensi blok dan mengira jisim dan jumlahnya, ketumpatannya ditentukan (2.68 g/cm³).
Walau bagaimanapun, apabila memeriksa jadual berangka bahan, ini menunjukkan bahawa ketumpatan aluminium adalah 2.7 g/cm³. Dengan cara ini, kesilapan mutlak dan peratusan akan dikira seperti berikut:
EA = 2.7 - 2.68
EA = 0.02 g/cm³.
EP = (0.02/2.7) x 100%
EP = 0.74%
3- Menghadiri acara
Diandaikan bahawa 1.000.000 orang akan pergi ke acara tertentu. Walau bagaimanapun, bilangan orang yang sebenar yang pergi ke acara ini ialah 88.000. Kesalahan mutlak dan peratusan akan menjadi berikut:
Boleh melayani anda: pemboleh ubah rawak: konsep, jenis, contohEA = 1.000.000 - 88.000
EA = 912.000
EP = (912,000/1,000,000) x 100%
EP = 91.2%
4. Jatuh bola
Masa yang dikira mesti mengambil bola untuk sampai ke tanah setelah dilemparkan pada jarak 4 meter adalah 3 saat.
Walau bagaimanapun, pada masa percubaan, didapati bola mengambil masa 2.1 saat untuk mencapai tanah.
EA = 3 - 2.1
EA = 0.9 saat
EP = (0.9/2.1) x 100%
EP = 42.8%
5. Ia memerlukan kereta untuk tiba
Dianggarkan bahawa jika kereta berjalan sejauh 60 km, ia akan mencapai tujuannya dalam masa 1 jam. Walau bagaimanapun, dalam kehidupan sebenar, kereta mengambil masa 1.2 jam untuk mencapai tujuannya. Kesalahan peratusan pengiraan masa ini akan dinyatakan seperti berikut:
EA = 1 - 1.2
EA = -0.2
EP = (-0.2/1.2) x 100%
Ep = -16%
6. Panjang mengukur
Sebarang panjang diukur dengan nilai 30 cm. Mengesahkan pengukuran panjang ini jelas bahawa terdapat kesilapan 0.2 cm. Kesalahan peratusan dalam kes ini akan ditunjukkan seperti berikut:
EP = (0.2/30) x 100%
EP = 0.67%
7. Panjang jambatan
Pengiraan panjang jambatan mengikut pesawatnya adalah 100 m. Walau bagaimanapun, apabila mengesahkan panjang ini, sekali dibina, jelas bahawa ia sebenarnya 99.8 m panjang. Kesalahan peratusan akan dibuktikan dengan cara ini.
EA = 100 - 99.8
EA = 0.2 m
EP = (0.2/99.8) x 100
EP = 0.2%
8. Diameter skru
Kepala skru yang dihasilkan standard adalah diameter 1 cm.
Boleh melayani anda: Pengagihan seragam yang berterusan: Ciri, contoh, aplikasiWalau bagaimanapun, apabila mengukur diameter ini, diperhatikan bahawa kepala skru benar -benar mempunyai 0.85 cm. Kesalahan peratusan adalah seperti berikut:
EA = 1 - 0.85
EA = 0.15 cm
EP = (0.15/0.85) x 100
EP = 17.64%
9. Berat objek
Menurut jumlah dan bahannya, dianggarkan bahawa berat objek tertentu adalah 30 kilogram. Sebaik sahaja objek dianalisis, diperhatikan bahawa berat badannya adalah 32 kilogram.
Dalam kes ini, nilai ralat peratusan digambarkan seperti berikut:
EA = 30 - 32
EA = -2 kilo
Ep = (2/32) x 100
EP = 6.25%
10. Pengukuran keluli
Di makmal lembaran keluli dipelajari. Apabila mengukur dimensi lembaran dan mengira jisim dan kelantangannya, ketumpatan yang sama (3.51 g/cm³) ditentukan.
Walau bagaimanapun, apabila memeriksa jadual berangka bahan, ini menunjukkan bahawa ketumpatan keluli adalah 2.85 g/cm³. Dengan cara ini, kesilapan mutlak dan peratusan akan dikira seperti berikut:
EA = 3.51 - 2.85
EA = 0.66 g/cm³.
EP = (0.66/2.85) x 100%
EP = 23.15%
Rujukan
- Kesalahan peratusan. Pulih dari Mathsisfun.com
- Cara mengira kesilapan peratus. Pulih dari pemikiran.com

