Ciri, contoh dan latihan yang berterusan

The Pemboleh ubah berterusan Ia adalah salah satu yang boleh mengambil jumlah nilai berangka yang tidak terhingga antara dua nilai yang diberikan, walaupun kedua -dua nilai tersebut sewenang -wenangnya ditutup. Mereka digunakan untuk menggambarkan atribut yang boleh diukur; contohnya ketinggian dan berat badan. Nilai yang diambil oleh pemboleh ubah berterusan boleh menjadi nombor rasional, nombor sebenar atau nombor kompleks, walaupun kes terakhir ini kurang kerap dalam statistik. 

Ciri utama pembolehubah berterusan ialah antara dua nilai rasional atau nyata selalu dapat dijumpai, dan antara yang lain dan yang pertama dapat mencari nilai lain, dan sebagainya.

Rajah 1. Lengkung mewakili pengedaran berterusan dan bar yang bijak. Sumber: Pixabay

Sebagai contoh, katakan pembolehubah berat dalam kumpulan di mana berat terbesar mempunyai 95 kg dan berat 48 kg terendah; Itu akan menjadi julat pemboleh ubah dan bilangan nilai yang mungkin adalah tak terbatas.

Contohnya antara 50.00 kg dan 50.10 kg mungkin 50.01. Tetapi antara 50.00 dan 50.01 ukuran mungkin 50,005. Itu adalah pemboleh ubah yang berterusan. Sebaliknya, jika dalam kemungkinan berat badan mengukur satu ketepatan perpuluhan ditubuhkan maka pembolehubah yang digunakan akan bijaksana.

Pembolehubah berterusan tergolong dalam kategori pembolehubah kuantitatif, kerana mereka mempunyai nilai berangka yang berkaitan. Dengan nilai berangka ini adalah mungkin untuk melaksanakan operasi matematik dari aritmetik dengan kaedah pengiraan infinitesimal. 

[TOC]

Contoh

Kebanyakan pembolehubah fizik adalah pembolehubah yang berterusan, di antaranya kita boleh menamakan: panjang, masa, kelajuan, pecutan, tenaga, suhu dan lain -lain.

Pembolehubah berterusan dan pembolehubah diskret

Dalam statistik, pelbagai jenis pembolehubah boleh ditakrifkan, baik kualitatif dan kuantitatif. Pembolehubah berterusan tergolong dalam kategori terakhir ini. Dengan mereka adalah mungkin untuk melaksanakan operasi aritmetik dan pengiraan.

Contohnya pemboleh ubah h, sepadan dengan orang yang mempunyai ketinggian antara 1.50 m dan 1.95 m, ia adalah pemboleh ubah berterusan. 

Mari kita bandingkan pembolehubah ini dengan yang lain: bilangan kali yang mahal dalam pelancaran mata wang, yang akan kita panggil n.

Pembolehubah n Anda boleh mengambil nilai antara 0 dan tak terhingga n Ia bukan pemboleh ubah berterusan kerana ia tidak dapat mengambil nilai 1.3 atau 1.5, kerana antara nilai 1 dan 2 tidak ada yang lain. Ini adalah contoh Pemboleh ubah diskret.

Menjalankan pembolehubah berterusan

Pertimbangkan contoh berikut: Mesin menghasilkan perlawanan fosforus dan bungkusnya di dalam kotaknya. Dua pembolehubah statistik ditakrifkan:

Boleh melayani anda: proses isobaric: formula, persamaan, eksperimen, latihan

Variabel 1: L = Plose Panjang.

Variabel 2: n = bilangan babi setiap kotak.

Panjang perlawanan nominal ialah 5.0 cm dengan toleransi 0.1 cm. Bilangan babi per kotak adalah 50 dengan toleransi 3.

a) menunjukkan julat nilai yang boleh diambil L dan N.

b) Berapa banyak nilai yang boleh anda ambil L?

c) Berapa banyak nilai yang boleh anda ambil n?

Katakan dalam setiap kes jika ia adalah pemboleh ubah yang bijak atau berterusan.

Penyelesaian

Nilai -nilai L Mereka difahami dalam selang waktu [5,0-0.1; 5.0+0.1]; itu adalah untuk mengatakan bahawa nilai L berada dalam selang [4.9 cm; 5.1 cm] dan pemboleh ubah L Anda boleh mengambil nilai tak terhingga antara kedua -dua langkah ini. Ia adalah pemboleh ubah yang berterusan.

Nilai pemboleh ubah n berada dalam selang [47; 53]. Pembolehubah n Ia hanya boleh mengambil 6 nilai yang mungkin dalam selang toleransi, maka ia adalah pemboleh ubah yang bijak.

Latihan taburan kebarangkalian

Sekiranya sebagai tambahan berterusan, nilai -nilai yang diambil oleh pemboleh ubah telah mengaitkan kebarangkalian kejadian tertentu, maka itu adalah Pemboleh ubah rawak berterusan. Sangat penting untuk membezakan sama ada pembolehubah adalah bijak atau berterusan, kerana model probabilistik terpakai antara satu sama lain adalah berbeza.

Pemboleh ubah rawak yang berterusan ditakrifkan sepenuhnya apabila nilai yang mereka dapat dianggap diketahui, dan kebarangkalian bahawa masing -masing harus berlaku.

-Latihan 1 kebarangkalian

Kilang perlawanan menjadikannya sedemikian rupa sehingga panjang tongkat selalu antara nilai 4.9 cm dan 5.1 cm, dan sifar dari nilai -nilai ini. Terdapat kebarangkalian mendapatkan tongkat yang mengukur antara 5.00 dan 5.05 cm, walaupun kita juga boleh mengeluarkan salah satu daripada 5.0003 cm. Adakah nilai -nilai ini sama -sama?.

Boleh melayani anda: Ketumpatan relatif: pengiraan, contoh, latihan

Penyelesaian

Katakan ketumpatan kebarangkalian seragam. Seterusnya, peluang untuk mencari fosforus dengan panjang tertentu disenaraikan:

-Bahawa fosforus berada dalam julat [4,9; 5,1] mempunyai kebarangkalian = 1 (atau 100%), kerana mesin tidak mengambil perlawanan daripada nilai tersebut.

-Mencari fosforus yang antara 4.9 dan 5.0 mempunyai kebarangkalian = ½ = 0.5 (50%), kerana ia adalah separuh daripada julat panjang.

-Dan kebarangkalian bahawa perlawanan mempunyai panjang antara 5.0 dan 5.1 juga 0.5 (50%)

-Adalah diketahui bahawa tidak ada tongkat fosforus yang mempunyai panjang antara 5.0 dan 5.2. Kebarangkalian: Zero (0%).

Kebarangkalian mencari tongkat dalam julat tertentu

Sekarang mari kita perhatikan kebarangkalian berikut p untuk mendapatkan tongkat yang panjangnya antara l₁ dan l₂:

 P = (l₂ -L₁) /(L_Maks - L_min)

-P bahawa perlawanan mempunyai panjang antara 5.00 dan 5.05 dilambangkan sebagai P ([5.00; 5.05]):

P ([5.00; 5.05]) = (5.05 - 5.00)/(5.1 - 4.9) = 0.05/0.2 = ¼ = 0.25 (25%)

-P bahawa Cerrillo mempunyai panjang antara 5.00 dan 5.01 adalah:

P ([5.00; 5.01]) = (5.00 - 5.01)/(5.1 - 4.9) = 0.01/0.2 = 1/20 = 0.05 (5 %)

-P bahawa Cerrillo mempunyai panjang antara 5,000 dan 5,001 lebih rendah:

P (5,000; 5,001) = 0.001/0.2 = 1/200 = 0.005 (0.5%)

Sekiranya kita terus mengurangkan selang waktu untuk mendekati lebih banyak hingga 5.00, kebarangkalian bahawa tongkat mempunyai tepat 5.00 cm adalah sifar (0%). Apa yang kita ada ialah kebarangkalian mencari perlawanan dalam julat tertentu.

Kebarangkalian mencari beberapa tongkat dalam julat tertentu

Sekiranya peristiwa bebas, kebarangkalian bahawa dua batang berada dalam julat tertentu adalah hasil kebarangkalian mereka.

-Kebarangkalian bahawa dua batang antara 5.0 dan 5.1 ialah 0.5*0.5 = 0.25 (0.25%)

-Kebarangkalian bahawa 50 tongkat antara 5.0 dan 5.1 adalah (0.5)^50 = 9 × 10^-16, yang hampir tidak.

-Kebarangkalian bahawa 50 tongkat antara 4.9 dan 5.1 adalah (1)^50 = 1 (100%)

-Latihan 2 kebarangkalian

Dalam contoh terdahulu, andaian dibuat bahawa kebarangkalian seragam dalam selang yang diberikan, namun ia tidak selalu berlaku.

Boleh melayani anda: tekanan hidrostatik: formula, pengiraan, contoh, latihan

Dalam kes mesin sebenar yang menghasilkan tongkat, kemungkinan bahawa tongkat berada dalam nilai pusat lebih besar daripada salah satu nilai yang melampau. Dari sudut pandangan matematik ini dimodelkan dengan fungsi f (x) yang dikenali sebagai ketumpatan kebarangkalian.

Kebarangkalian bahawa ukuran antara a dan b dikira oleh integral fungsi f (x) yang ditetapkan antara a dan b. 

Sebagai contoh, katakan kita ingin mencari fungsi f (x), yang mewakili taburan seragam antara nilai 4.9 dan 5.1 latihan 1. 

Sekiranya taburan kebarangkalian seragam, maka f (x) adalah sama dengan c malar, yang ditentukan mengambil integral antara 4.9 dan 5.1 c. Oleh kerana integral ini adalah kebarangkalian, jadi hasilnya mestilah 1.

Rajah 2. Ketumpatan kebarangkalian seragam. (Huraian sendiri)

Yang bermaksud bahawa C bernilai 1/0.2 = 5. Dengan kata lain, fungsi ketumpatan kebarangkalian seragam adalah f (x) = 5 jika 4.9≤x≤5.1 dan 0 dari julat ini. Rajah 2 menunjukkan fungsi ketumpatan kebarangkalian seragam.

Perhatikan seperti selang lebar yang sama (contohnya 0.02) kebarangkalian adalah sama di tengah seperti pada akhir julat pembolehubah berterusan L (Panjang jeruk).

Model yang lebih realistik akan menjadi fungsi ketumpatan kebarangkalian seperti yang berikut:

-F (x) = -750 ((x-5.0)^2-0.01) jika 4.9≤x≤5,1

-0 Di luar julat ini 

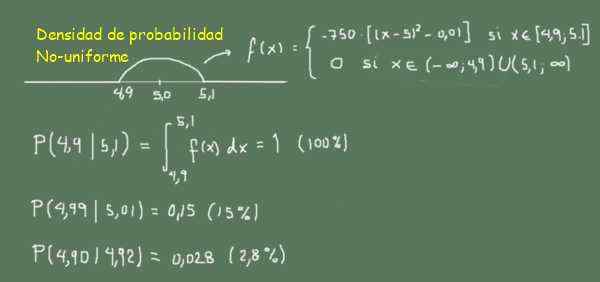Rajah 3. Fungsi ketumpatan kebarangkalian bukan seragam. (Huraian sendiri)

Dalam Rajah 3 ia dapat dilihat sebagai kebarangkalian mencari tongkat antara 4.99 dan 5.01 (lebar 0.02) lebih besar daripada mencari tongkat antara 4.90 dan 4.92 (lebar 0.02)

Rujukan

1. Dinov, Ivo. Pembolehubah rawak diskret dan pengagihan kebarangkalian. Pulih dari: stat.UCLA.Edu
2. Pembolehubah rawak yang diskret dan berterusan. Pulih dari: ocw.MIT.Edu
3. Pembolehubah rawak diskret dan pengagihan kebarangkalian. Pulih dari: laman utama.DDMS.Uiowa.Edu
4. H. Peshro. Pengenalan kepada kebarangkalian. Pulih dari: Kursus kebarangkalian.com
5. Mendenhall, w. 1978. Statistik untuk Pentadbiran dan Ekonomi. Kumpulan editorial Ibero -Amerika. 103-106.
6. Masalah pemboleh ubah rawak dan model kebarangkalian. Pulih dari: ugr.adalah.
7. Wikipedia. Pemboleh ubah berterusan. Pulih dari Wikipedia.com
8. Wikipedia. Pemboleh ubah statistik. Pulih dari Wikipedia.com.