Matematik

Variasi berkadar

Variasi berkadar

Apakah variasi berkadar?

Variasi berkadar antara dua pembolehubah "x" dan "y" berlaku apabila, dengan mengalikan salah satu daripada mereka dengan satu pemalar, yang lain juga didarabkan atau dibahagikan dengan pemalar yang sama. Banyak situasi dunia sebenar dapat diterangkan dengan baik dengan mereka.

Perkadaran antara pembolehubah boleh langsung atau terbalik. Secara langsung, hubungannya adalah jenis:

y = k ∙ x

Atau setara:

K = y/x

Di mana k adalah tetap dipanggil pemalar proporsional Sama ada nisbah perkadaran. Perhatikan bahawa jika "x" meningkat, "y" melakukannya dalam perkadaran yang sama, dan jika "x" berkurangan, ia juga akan "y". Apabila hubungan antara pembolehubah adalah graf, garis lurus diperolehi yang melalui asal sistem koordinat (lihat latihan yang diselesaikan kemudian).

Variasi langsung juga boleh berlaku di antara satu pemboleh ubah dan satu kuasa yang lain, sebagai contoh, "y" boleh berkadar terus dengan x2, x3 dan juga.

Sebaliknya, dalam perkadaran terbalik, pembolehubah dikaitkan melalui ungkapan:

x ∙ y = k

Ungkapan ini bermaksud bahawa produk pembolehubah adalah tetap. Semasa menggambarkan hubungan antara pembolehubah adalah hiperbola. Juga, jika produk pembolehubah dengan satu kuasa yang lain adalah malar, ia juga mewakili kes perkadaran terbalik, sebagai contoh:

x2∙ y = k; x3∙ y = k ..

Contoh

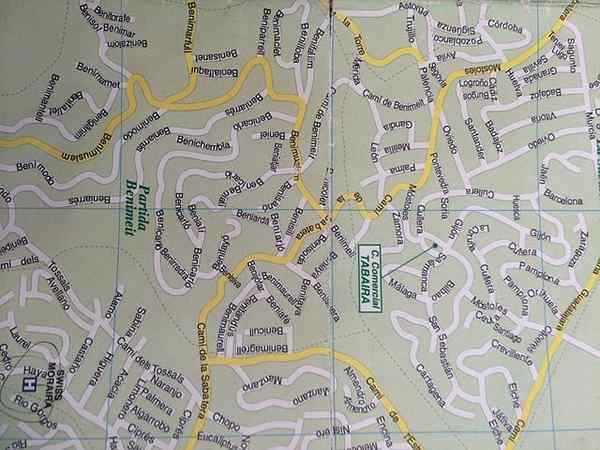Permohonan variasi berkadar adalah susun atur peta

Banyak undang -undang fizik dan kimia dinyatakan secara matematik sebagai perkadaran. Contohnya, daya yang menghasilkan musim bunga dan pemanjangan yang sama, hubungan antara tekanan dan kelantangan dalam gas pada suhu malar, tempoh pendulum mudah dan akar kuadrat panjangnya dan banyak lagi. Mengetahui model yang mengawal fenomena ini, anda dapat mengetahui tingkah laku anda untuk sebarang nilai pembolehubah.

Boleh melayani anda: Teorem kewujudan dan keunikan: demonstrasi, contoh dan latihan

Dan bukan hanya itu, mereka juga memohon dalam situasi yang banyak seperti ini:

  • Lulus corak pakaian saiz yang lebih kecil ke saiz yang lebih besar (atau sebaliknya).
  • Dalam faktor penukaran, untuk bergerak dari satu unit ke unit lain, seperti kilometer hingga batu, gelen ke liter dan banyak lagi.
  • Kirakan ramuan resipi untuk 6 orang yang mengetahui keperluan untuk 4 orang.
  • Tentukan jumlah cukai tertentu mengikut pendapatan yang diperoleh.
  • Dalam pengiraan minat mudah.
  • Semasa melukis pesawat secara berskala.
  • Apabila anda perlu mengira harga jumlah produk yang mengetahui harga unit.
  • Dalam persamaan segitiga.

Seterusnya, secara terperinci, terdapat dua situasi yang menarik di mana variasi berkadar dikenakan:

Contoh 1

Pada skala bandar, Hermitage Avenue mengukur 3.2 cm, sebagai panjang sebenar 400 m. Sebaliknya, jalan La Fuente, yang benar -benar mengukur 180 m panjang harus menarik dengan strok yang lebih pendek. Berapakah ukuran strok?

Kenyataan ini menawarkan maklumat lengkap mengenai ermita avenue: biarkan panjang sebenar jalan dan ℓ panjangnya di atas kapal terbang, kerana variasi adalah perkadaran langsung, ia harus:

L = k ∙ ℓ

Dari data di Hermitage Avenue, anda dapat mengetahui nilai malar perkadaran k, tetapi sebelum ia perlu meninggalkan semua panjang dalam unit yang sama:

3.2 cm = 0.032 m

Jadi:

400 m = k ∙ 0.032 m

Oleh itu, pemalar perkadaran adalah:

Boleh melayani anda: apakah unsur -unsur perumpamaan? (Bahagian)

K = 400/0.032 = 12500

Sekarang diketahui bahawa:

L = 12500 ∙ ℓ

Hasil ini ditafsirkan seperti berikut: panjang jalan -jalan di peta ini adalah 12500 kali lebih kecil daripada panjangnya. Oleh itu garis jalan La Fuente mengukur:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Contoh 2

Seorang penganalisis mempunyai jadual nilai berikut untuk pembolehubah "x" dan "y" yang diperoleh secara eksperimen dan ingin mengetahui sama ada data ini sesuai dengan model variasi berkadar langsung atau salah satu variasi berkadar songsang.

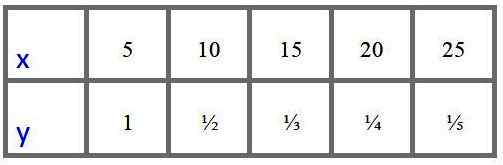
Apa yang perlu anda lakukan untuk mengetahui?

Di tempat pertama diperhatikan bahawa apabila "x" meningkat, "y" berkurangan, jadi ia mengesyaki perkadaran terbalik, dalam apa jua keadaan, untuk memastikan, penganalisis mempunyai pilihan untuk menilai sama ada quotient dan/x adalah malar (berkadar variasi langsung) atau jika produk x.dan tetap (variasi berkadar songsang).

Ujian dengan pilihan pertama:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Disimpulkan bahawa ia bukan variasi berkadar langsung, kerana quotient dan/x memberikan nilai yang berbeza untuk setiap beberapa data.

Kita perlu menyemak sama ada produk x ∙ adalah malar:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

Dan sebagai produk x ∙ y = 5 disimpulkan bahawa variasi adalah berkadar terbalik.

Maklumat ini berfungsi untuk mengetahui nilai -nilai yang tidak ada di dalam jadual, sebagai contoh, apakah nilai "y" apabila x = 30?

Dari x ∙ y = 5, "y" dibersihkan dan diganti x = 30:

y = 5/x

y = 5/30 = 1/6

Latihan diselesaikan

Sekiranya meter kain berharga 6.$ 75, dan mengetahui bahawa harga adalah berkadar terus dengan jumlah meter untuk membeli, cari:

Ia boleh melayani anda: antiderivatif: formula dan persamaan, contoh, latihan

a) Ekspresi algebra yang menghubungkan pembolehubah "harga pada $" dan "bilangan meter kain".

b) Sediakan jadual nilai dengan harga untuk kain 3, 6, 9, 12, 15 dan 18 meter.

c) graf nilai yang diperolehi.

Jawapan kepada

Biarkan "y" pembolehubah "harga pada $" dan "x" pembolehubah "kuantiti meter kain". Seperti berkadar terus, anda mesti:

y = k ∙ x

Untuk x = 1 meter, y = 6.$ 75, oleh itu k = 6.75 $/meter. Ini adalah harga unit kain, harga kain "x" yang lain diperoleh dengan mendarab dengan nilai ini, maka ungkapan algebra yang dicari adalah:

y = 6.75 ∙ x

Jawab b

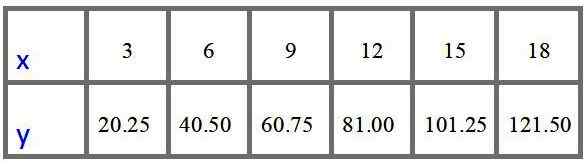
Jadual nilai dengan harga pada $ untuk 3, 6, 9, 12, 15 dan 18 meter adalah:

Jawab c

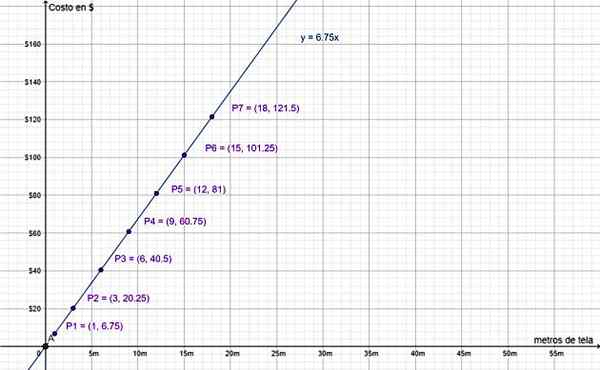
Akhirnya, graf nilai dalam jadual sebelumnya menyokong bahawa ia adalah variasi berkadar langsung:

Kos pada $ dan jumlah meter kain adalah jumlah berkadar secara langsung. Sumber: f. Zapata.

Perhatikan bahawa nilai (0.0) dimasukkan, kerana garis y = 6.75 ∙ x melewati asal -usul sistem koordinat, seperti yang dijelaskan sebelumnya. Masuk akal, kerana tidak membuat pembelian bersamaan dengan membeli 0 m kain, yang nilainya adalah 0 $.

Rujukan

  1. Larson, r. 2012. Pra-Sculpture. Ke -8. Edisi. Pembelajaran Cengage.
  2. Sekretariat Pendidikan Awam Mexico. Variasi berkadar. Diperolehi dari: PPS.K12.Atau.kita.
  3. Stewart, J. 2007. Pra-Kalkulasi: Matematik untuk Pengiraan. 5th. Edisi. Pembelajaran Cengage.
  4. Unam. Panduan Kajian: Matematik i. Pulih dari: dirre.Unam.mx.
  5. Zill, d. 2008. Pra-Kalkulasi dengan Kemajuan Pengiraan. Ke -4. Edisi. McGraw Hill.