Ciri dan sifat vektor, elemen, jenis, contoh

The vektor Mereka adalah entiti matematik yang mempunyai magnitud -positive -, biasanya disertai dengan unit ukuran, sebagai tambahan kepada arah dan makna. Ciri -ciri sedemikian sangat sesuai untuk menggambarkan kuantiti fizikal seperti kelajuan, kekuatan, pecutan dan banyak lagi.

Dengan vektor adalah mungkin untuk melaksanakan operasi seperti jumlah, penolakan dan produk. Bahagian ini tidak ditakrifkan untuk vektor dan bagi produk, terdapat tiga kelas yang akan kami terangkan kemudian: produk skalar atau titik, vektor atau produk silang dan produk skalar untuk vektor.

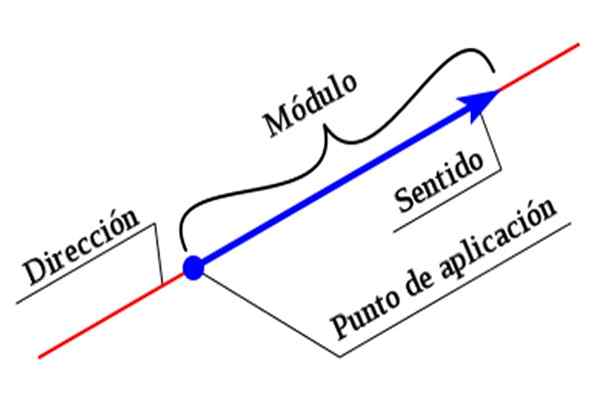Rajah 1. Unsur -unsur vektor. Sumber: Wikimedia Commons.

Untuk menggambarkan sepenuhnya vektor, perlu menunjukkan semua ciri -cirinya. Besarnya atau modul adalah nilai berangka yang disertakan dengan unit, sementara arah dan makna ditubuhkan dengan bantuan sistem koordinat.

Mari kita lihat contoh: Katakan pesawat terbang dari satu bandar ke bandar yang lain pada kadar 850 km/j ke arah. Di sini kita mempunyai vektor yang ditentukan sepenuhnya, kerana magnitud tersedia: 850 km/j, sementara arah dan makna adalah NE.

Vektor biasanya diwakili secara grafik oleh segmen garis berorientasikan, yang panjangnya berkadar dengan magnitud.

Walaupun untuk menentukan arah dan makna, garis rujukan diperlukan yang biasanya paksi mendatar, walaupun utara juga boleh diambil sebagai rujukan, seperti halnya kelajuan pesawat:

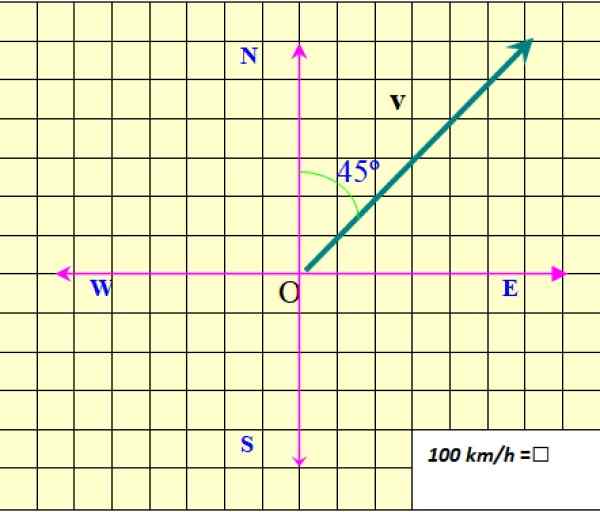Rajah 2. Vektor kelajuan. Sumber: f. Zapata.

Angka ini menunjukkan vektor kelajuan satah, yang dilambangkan sebagai v dalam berani, untuk membezakannya dari kuantiti skalar, yang hanya memerlukan nilai berangka dan beberapa unit yang akan ditentukan.

[TOC]

Unsur vektor

Seperti yang telah kita katakan, elemen vektor adalah:

-Magnitud atau modul, kadang -kadang juga dipanggil nilai mutlak atau standard vektor.

-Alamat

-Rasa

Dalam contoh Rajah 2, modul v Itu 850 km/j. Modul ini dilambangkan sebagai V tanpa berani, atau sebagai |v|, Di mana bar mewakili nilai mutlak.

Alamat v ditentukan berkenaan dengan utara. Dalam kes ini ia adalah 45º di utara timur (45º NE). Akhirnya hujung anak panah memberitahu arahan v.

Dalam contoh ini, asal vektor telah ditarik dengan bersamaan dengan sistem asal atau koordinat, ini dikenali sebagai Vektor yang dipautkan. Sebaliknya, jika asal vektor tidak sepadan dengan sistem rujukan, dikatakan bahawa ia adalah vektor percuma.

Harus diingat bahawa untuk menentukan sepenuhnya vektor, ketiga -tiga elemen ini mesti ditunjukkan, jika tidak, perihalan vektor tidak lengkap.

Komponen segi empat tepat vektor

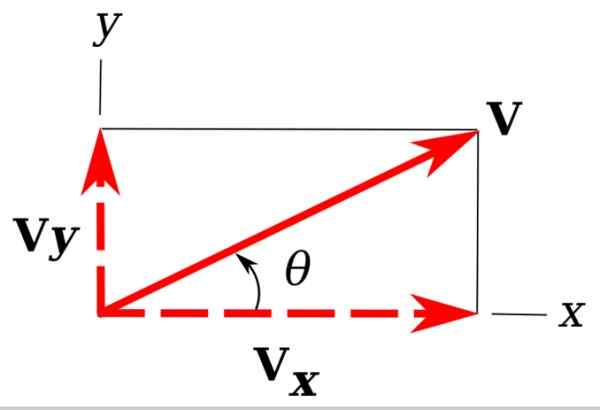Rajah 3. Komponen segi empat tepat vektor dalam pesawat. Sumber: Wikimedia Commons. Unther [cc by-sa 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Dalam imej kami telah mengembalikan contoh vektor kami v, yang ada dalam kapal terbang Xy.

Sangat mudah untuk melihat bahawa unjuran v pada paksi koordinat x dan y menentukan segitiga yang betul. Unjuran ini adalah v_dan dan v_x dan dipanggil komponen segi empat tepat v.

Cara untuk menunjukkan v Melalui komponen segi empat tepatnya seperti ini: v = x, v_dan>. Kurungan persegi ini digunakan dan bukannya kurungan untuk menekankan fakta bahawa ia adalah vektor dan bukan satu titik, kerana dalam hal ini tanda kurung akan digunakan.

Boleh melayani anda: James Chadwick: Biografi, Model Atom, Eksperimen

Sekiranya vektor berada dalam ruang tiga dimensi, satu lagi komponen diperlukan, supaya:

v = x, v_dan, v_z>

Mengetahui komponen segi empat tepat, magnitud vektor dikira, bersamaan dengan mencari hipotenus segitiga kanan yang kakinya v_x dan v_dan,. Melalui teorem Pythagoras ia mengikuti:

|v|² = (v_x)² +  (v_dan)²

Bentuk kutub vektor

Apabila magnitud vektor dikenali |v| Dan sudut θ yang bentuk ini dengan paksi rujukan, biasanya paksi mendatar, vektor sama -sama ditentukan. Kemudian dikatakan bahawa vektor dinyatakan dalam bentuk kutub.

Komponen segi empat tepat dalam kes ini mudah dikira:

v_x = |v|.cos θ

v_dan = |v|.sin θ

Menurut di atas, komponen segi empat tepat vektor kelajuan v pesawat akan menjadi:

v_x = 850 . cos 45º km/h = 601.04 km/j

v_dan = 850 . Sen 45º km/h = 601.04 km/j

Lelaki

Terdapat pelbagai jenis vektor. Terdapat vektor urat, kedudukan, anjakan, daya, medan elektrik, jumlah pergerakan dan banyak lagi. Seperti yang telah kita katakan, dalam fizik terdapat banyak magnitud vektor.

Bagi vektor yang mempunyai ciri -ciri tertentu, kita boleh menyebut jenis vektor berikut:

-Batal: Ini adalah vektor yang magnitudnya 0 dan yang dilambangkan sebagai 0. Ingat bahawa huruf berani melambangkan tiga ciri asas vektor, sementara huruf normal hanya mewakili modul.

Contohnya mengenai badan dalam keseimbangan statik, jumlah daya mestilah vektor null.

-Percuma dan dihubungkan: Vektor bebas adalah orang -orang yang asal dan ketibaannya adalah sepasang titik satah atau ruang, tidak seperti vektor yang dipautkan, yang asalnya bertepatan dengan sistem rujukan yang digunakan untuk menggambarkannya.

Pasangan atau momen yang dihasilkan oleh beberapa kuasa adalah contoh yang baik dari vektor percuma, kerana tork tidak terpakai pada titik tertentu.

-Peralatan: Mereka adalah dua vektor percuma yang berkongsi ciri -ciri yang sama. Oleh itu mereka mempunyai magnitud, arah dan makna yang sama.

-Coplanares atau coplanarios: vektor yang tergolong dalam pesawat yang sama.

-Berlawanan: vektor dengan magnitud dan arah yang sama, tetapi deria bertentangan. Vektor menentang vektor v Ia adalah vektor -v Dan jumlah kedua -duanya adalah vektor null: v + (-v) = 0.

-Serentak: vektor yang garis tindakannya melewati titik yang sama.

-Gelongsor: Adakah vektor -vektor yang mana titik permohonannya dapat meluncur di sepanjang garis tertentu.

-Colineal: vektor yang terletak di barisan yang sama.

-Persatuan: Vektor -vektor yang modulnya adalah 1.

Vektor unit ortogonal

Terdapat jenis vektor yang sangat berguna dalam fizik yang dipanggil vektor unit ortogonal. Vektor unit ortogonal mempunyai modul yang sama dengan 1 dan unit boleh menjadi apa -apa, contohnya kelajuan, kedudukan, kekuatan atau lain -lain.

Terdapat satu set vektor khas yang membantu dengan mudah mewakili vektor lain dan melakukan operasi dengan mereka: mereka adalah vektor unit ortogonal Yo, J dan k, Persatuan dan tegak lurus antara satu sama lain.

Dalam dua dimensi, vektor ini diarahkan sepanjang pengertian positif kedua -dua paksi x Sehingga paksi dan. Dan dalam tiga dimensi vektor unit ditambah ke arah paksi z positif. Mereka diwakili seperti berikut:

Boleh melayani anda: apakah struktur penyelidikan dokumentari?

Yo =

J =

k =

Vektor boleh diwakili oleh vektor unit Yo, J dan k seperti berikut:

v = v_x Yo + v_dan J + v_z k

Contohnya vektor halaju v Dari contoh sebelumnya, anda boleh menulis sebagai:

v = 601.04 Yo + 601.04 J km/h

Komponen dalam k Tidak perlu, kerana vektor ini berada dalam pesawat.

Jumlah vektor

Jumlah vektor kelihatan sangat kerap dalam pelbagai situasi, contohnya apabila anda ingin mencari daya yang dihasilkan pada objek yang dipengaruhi oleh pelbagai daya. Untuk memulakan anda mempunyai dua vektor percuma atau dan v Di pesawat, seperti yang berikut menunjukkan kiri:

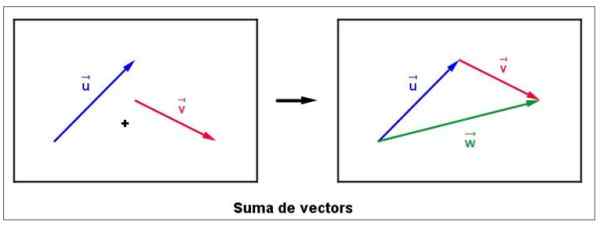Rajah 4. Jumlah grafik dua vektor. Sumber: Wikimedia Commons. Lluc Cabanach [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)].

Dia segera bergerak ke vektor v, tanpa mengubah magnitud, arah atau makna, sehingga ia berasal dari akhir atau.

Vektor jumlah dipanggil W dan ditarik bermula dari u yang berakhir v, Menurut angka yang betul. Penting untuk diperhatikan bahawa magnitud vektor W Tidak semestinya jumlah magnitud v dan atau.

Sekiranya ia dicerminkan dengan teliti dalam hal ini, satu -satunya peristiwa apabila magnitud vektor yang dihasilkan adalah jumlah magnitud tambahan, ketika kedua -dua penagih berada dalam arah yang sama dan mempunyai makna yang sama.

Dan apa yang berlaku jika vektor tidak percuma? Ia juga sangat mudah untuk menambahkannya. Cara untuk dilakukan ialah menambahkan komponen komponen, atau kaedah analisis.

Sebagai contoh, mari kita pertimbangkan vektor angka berikut, perkara pertama adalah untuk menyatakannya dari salah satu bentuk Cartesian yang dijelaskan sebelum ini:

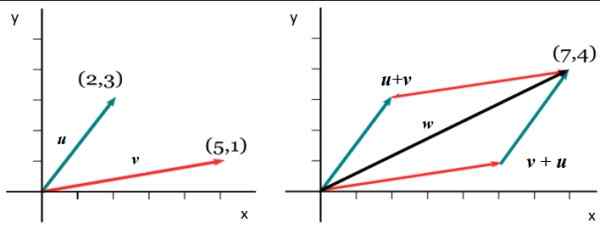Rajah 5. Jumlah dua vektor yang berkaitan. Sumber: Wikimedia Commons.

v =

atau =

Untuk mendapatkan komponen dalam x vektor menambah W, Komponen masing -masing ditambah dalam x dari v dan atau: W_x = 5+2 = 7. Dan untuk mendapatkan W_dan Prosedur analog diikuti: w_dan = 1+3. Oleh itu:

atau =

Sifat jumlah vektor

-Jumlah dua atau lebih vektor menghasilkan vektor lain.

-Ia adalah komutatif, perintah penambahan tidak mengubah jumlahnya, supaya:

atau + v = v + atau

-Unsur neutral jumlah vektor adalah vektor null: v + 0 = v

-Penolakan dua vektor ditakrifkan sebagai jumlah yang bertentangan: v - u = v + (-or)

Contoh vektor

Seperti yang telah kita katakan, terdapat banyak kuantiti vektor dalam fizik. Antara yang paling terkenal ialah:

-Kedudukan

-Pemindahan

-Kelajuan purata dan kelajuan serta -merta

-Pecutan

-Kuasa

-Jumlah pergerakan

-Tork atau momen kekuatan

-Dorongan

-medan elektrik

-Medan magnet

-Momen magnet

Sebaliknya mereka bukan vektor tetapi memanjat:

-Masa

-Massa

-Suhu

-Kelantangan

-Ketumpatan

-Kerja mekanikal

-Tenaga

-Haba

-Kuasa

-voltan

-Arus elektrik

Operasi lain antara vektor

Sebagai tambahan kepada jumlah dan penolakan vektor, terdapat tiga operasi lain antara vektor yang sangat penting, kerana mereka menimbulkan magnitud fizikal yang sangat penting:

-Produk skalar untuk vektor.

-Produk skalar atau produk titik antara vektor

-Dan produk salib atau vektor antara dua vektor.

Produk skalar untuk vektor

Pertimbangkan undang -undang kedua Newton, yang menyatakan bahawa memaksa F dan pecutan ke Mereka berkadar. Pemalar perkadaran adalah jisim m Oleh itu, objek itu:

F = m.ke

Doh adalah skalar; Bagi bahagiannya, kekuatan dan pecutan adalah vektor. Oleh kerana daya diperolehi dengan mengalikan jisim dengan pecutan, itu adalah hasil produk skalar oleh vektor.

Boleh melayani anda: Contoh kerangka teoritis

Jenis produk ini selalu menghasilkan vektor. Di sini contoh lain: jumlah pergerakan. Menjadi P Jumlah pergerakan vektor, v Vektor halaju dan seperti biasa, m adalah jisim:

P = m.v

Produk skalar atau produk titik antara vektor

Kami telah meletakkan kerja mekanikal dalam senarai magnitud yang bukan vektor. Walau bagaimanapun, kerja dalam fizik adalah hasil operasi antara vektor yang disebut produk skalar, produk dalaman atau produk titik.

Jadilah vektor v dan atau, Produk titik atau pendakian ditakrifkan di antara mereka:

v∙atau = |v| ∙ |atau |.cos θ

Menjadi θ sudut di antara mereka. Dari persamaan yang ditunjukkan, segera disimpulkan bahawa hasil produk titik adalah skalar dan juga jika kedua -dua vektor berserenjang, produk skalar mereka adalah 0.

Kembali ke kerja mekanikal W, Ini adalah produk skalar antara vektor kekuatan F dan anjakan vektor ℓ.

W = F∙ℓ                  

Apabila vektor tersedia dari segi komponen mereka, produk titik juga sangat mudah untuk dikira. Yeah v = x, v_dan, v_z > dan atau = x, atau_dan, atau_z >, Produk titik antara keduanya adalah:

v∙atau = v_x atau_x + v_dan atau_dan + v_z atau_z

Produk titik antara vektor adalah komutatif, oleh itu:

v∙atau = atau∙v

Produk silang atau produk vektor antara vektor

Yeah v dan anda adalah dua contoh vektor kami, produk vektor ditakrifkan sebagai:

v x atau = W

Ia segera mengikuti bahawa produk silang menghasilkan vektor, yang modulnya ditakrifkan sebagai:

|v x u | = | V | . | u |. sin θ

Di mana θ Ia adalah sudut antara vektor.

Oleh itu, produk silang tidak komutatif v x u ≠ u x v. Sebenarnya v x U = - (u x V).

Jika kedua -dua contoh vektor dinyatakan dari segi vektor unit, pengiraan produk vektor difasilitasi:

v = v_x Yo + v_dan J + v_z k

atau = u_x Yo + atau_dan J + atau_z k

Produk silang antara vektor unit

Produk silang antara vektor unit yang sama adalah batal, kerana sudut di antara mereka adalah 0º. Tetapi di antara vektor unit yang berbeza, sudut di antara mereka adalah 90º dan dosa 90º = 1.

Skim berikut membantu mencari produk ini. Ke arah anak panah itu masuk akal positif dan ke arah yang bertentangan:

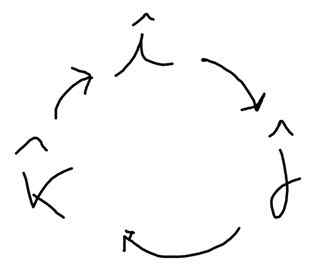
Yo x J = k, j x k = Yo; k x Yo = J; J x i = -k; k x J = -Yo; Yo x k = -J

Memohon harta pengedaran, yang tetap sah untuk produk di kalangan vektor ditambah sifat vektor unit, anda mempunyai:

v x atau = (v_x Yo + v_dan J + v_z k) X (u_x Yo + atau_dan J + atau_z k) =  

= (v_danatau_z - v_zatau_dan )Yo + (v_zatau_x - v_xatau_z )J + (v_xatau_dan - v_danatau_x )k

Latihan yang diselesaikan

- Latihan 1

Diberi vektor:

v = -5 Yo + 4J + 1 k

atau = 2 Yo -3 J + 7k

Apa yang harus menjadi vektor W Jadi jumlahnya v + atau + W hasilnya 6 Yo +8 J -10k?

Penyelesaian

-5 Yo + 4J + 1 k

2 Yo -3 J + 7k

 W_x Yo + W_dan J + W_z k  +

--

6Yo + 8 J -10 k

Oleh itu ia mesti dipenuhi bahawa:

-5 +2 + w_x = 6 → W_x = 9

4-3 + w_dan = 8 → W_dan = 7

1 + 7 + w_z = -10 → W_z = -18

Jawapannya ialah: W = 9 Yo +7 J - 18k

- Latihan 2

Apakah sudut antara vektor v dan atau Latihan 1?

Penyelesaian

Kami akan menggunakan produk skalar. Kami ada:

cos θ = v∙atau / |v| ∙ |atau|

v∙atau= -10 -12+7 = -15

|v| = √ (-5)² +4² +1²= √42 = 6.48

|atau| = √2² +(-3)² +7²= √62 = 7.87

Menggantikan nilai -nilai ini:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → θ = 107.1st

Rujukan

1. Figueroa, d. (2005). Siri: Fizik untuk Sains dan Kejuruteraan. Jilid 1. Kinematik. Diedit oleh Douglas Figueroa (USB).
2. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6th. Ed Prentice Hall.
3. Rex, a. 2011. Asas Fizik. Pearson.
4. Sears, Zemansky. 2016. Fizik universiti dengan fizik moden. Ke -14. Ed. Jilid 1.
5. Serway, r., Jewett, J. 2008. Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage.