Ciri -ciri vektor serentak, contoh dan latihan

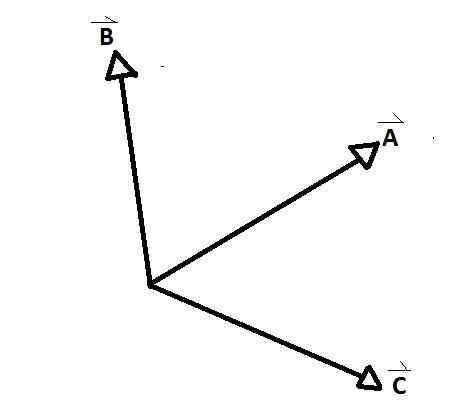
The vektor serentak Mereka adalah kumpulan vektor yang paksi bertepatan pada satu titik, membentuk antara setiap pasangan mereka sudut dalaman dan luaran. Contoh yang jelas diperhatikan pada angka yang lebih rendah, di mana A, B dan C adalah vektor serentak antara satu sama lain.

D dan e tidak seperti selebihnya tidak. Terdapat sudut yang terbentuk di kalangan vektor serentak AB, AC dan CB. Sudut hubungan antara vektor dipanggil.

[TOC]

Ciri -ciri

-Mereka mempunyai titik yang sama, yang bertepatan dengan asal usul mereka: semua magnitud vektor serentak bermula dari titik umum kepada ekstrem masing -masing.

-Asal dianggap sebagai titik tindakan vektor: titik tindakan mesti ditubuhkan yang akan terjejas secara langsung oleh setiap vektor serentak.

-Domain anda dalam pesawat dan ruang adalah R² dan r³ masing -masing: Vektor serentak bebas untuk menampung seluruh ruang geometri.

-Membolehkan notasi yang berbeza dalam kumpulan vektor yang sama. Menurut cabang pengajian, notasi yang berbeza hadir dalam operasi dengan vektor.

Jenis vektor

Cabang vektor mempunyai pelbagai subdivisi, di antara beberapa yang mereka boleh dilantik: selari, tegak lurus, coplanarios, sepadan, bertentangan dan kesatuan. Vektor serentak muncul dalam senarai ini dan seperti semua yang dilantik sebelum ini, mereka mempunyai banyak aplikasi dalam sains yang berbeza.

Mereka sangat biasa dalam kajian vektor, kerana mereka mewakili generalisasi yang menguntungkan dalam operasi dengan mereka. Kedua -duanya dalam satah dan di angkasa, vektor serentak adalah untuk kegunaan semasa untuk perwakilan unsur -unsur yang berbeza dan mengkaji pengaruh mereka terhadap sistem tertentu.

Notasi vektor

Terdapat pelbagai cara untuk mewakili elemen vektor. Yang utama dan paling terkenal ialah:

Cartesian

Cadangan dengan pendekatan matematik yang sama, menandakan vektor dengan senarai yang sepadan dengan magnitud setiap paksi (x, y, z)

A: (1, 1, -1) Ruang A: (1, 1) Rancangan

Kutub

Mereka hanya berfungsi untuk menunjukkan vektor dalam pesawat, walaupun dalam pengiraan integral komponen kedalaman diberikan. Ia terdiri daripada magnitud linear r dan sudut berkenaan dengan paksi kutub Ɵ.

Boleh melayani anda: Statistik inferens: sejarah, ciri, apa itu, contohnya

A: (3, 45⁰ ) Rancang A: (2, 45⁰ , 3) ruang

Analisis

Tentukan magnitud vektor melalui versor. Versor (R & E + K) mewakili vektor unit yang sepadan dengan paksi X, y dan

A: 3i + 2j - 3k

Sfera

Ia serupa dengan notasi kutub, tetapi dengan penambahan sudut kedua yang menyapu di atas kapal terbang Xy dilambangkan oleh δ.

A: (4, 60^{Sama ada} , π/4)

Operasi dengan vektor serentak

Vektor serentak kebanyakannya digunakan untuk menentukan operasi antara vektor, kerana lebih mudah untuk membandingkan unsur -unsur vektor apabila ia berlaku secara serentak.

Jumlah (a + b)

Jumlah vektor serentak bertujuan untuk mencari vektor yang dihasilkan V_r. Yang, menurut cabang pengajian, sepadan dengan tindakan akhir

Contohnya: 3 rentetan terikat a, b, c ke kotak, setiap hujung tali berada di tangan subjek. Setiap satu daripada 3 mata pelajaran mesti menarik tali ke arah selain daripada 2 yang lain.

A: (kapak, ay, az) b: (bx, by, bz) c: (cx, cy, cz)

A+b+c = (ax+bx+cx; ay+by+cy; az+bz+cz) = V_r

Kotak hanya boleh bergerak ke satu arah, oleh itu V_r akan menunjukkan arah dan rasa anjakan kotak.

Perbezaan (a - b)

Terdapat banyak kriteria mengenai perbezaan antara vektor, banyak penulis memilih untuk mengecualikannya dan mendakwa bahawa hanya jumlah antara vektor yang ditetapkan, di mana perbezaannya adalah jumlah vektor yang bertentangan. Kebenarannya ialah vektor algebra boleh ditolak.

A: (kapak, ay, az) b: (bx, by, bz)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-by); AZ + (-bz)]

Produk skalar (a . B)

Juga dikenali sebagai produk punto, menghasilkan nilai skalar yang boleh dikaitkan dengan beberapa magnitud mengikut cawangan kajian.

Untuk geometri menunjukkan kawasan paralelogram yang dibentuk oleh sepasang vektor serentak melalui kaedah paralelogram. Untuk fizik mekanikal mentakrifkan kerja yang dilakukan oleh kekuatan F Dengan menggerakkan badan jauh ΔR.

Ia boleh melayani anda: Kompaun berkadar: Penjelasan, tiga peraturan kompaun, latihan

ѡ = f . ΔR

Seperti namanya, ia menghasilkan nilai skalar dan ditakrifkan seperti berikut:

Jadilah vektor a dan b

A: (kapak, ay, az) b: (bx, by, bz)

-Bentuk Analisis:

(Kepada . B) = | a |.| B |.Cos θ

Di mana θ adalah sudut dalaman antara kedua -dua vektor

-Bentuk algebra:

(Kepada . B) = (kapak.Bx + ay.oleh + az.Bz)

Produk vektor (a x b)

Produk vektor atau titik antara dua vektor, mentakrifkan vektor ketiga C yang mempunyai kualiti tegak lurus B dan C. Dalam fizik mentakrifkan tork vektor τ Elemen asas dinamik putaran.

-Bentuk Analisis:

| A X B | = | A |.| B |.Sin θ

-Bentuk algebra:

(A x b) = = (Kapak . oleh - ay . bx)- (kapak . BZ - AZ . bx) J + (Kapak . oleh - ay . bx) k

-Pergerakan relatif: r_A/b

Asas relativiti adalah pergerakan relatif dan vektor serentak adalah asas pergerakan relatif. Anda boleh menyimpulkan kedudukan, kelajuan dan pecutan relatif dengan menggunakan urutan idea berikut.

r _A/b = r_Ke - r_B    ; Kedudukan relatif mengenai b

v _A/b = v_Ke - v_B  ; Kelajuan relatif menghormati b

ke _A/b = a_Ke - ke_B  ; Pecutan relatif menghormati b

Contoh: Latihan yang diselesaikan

Latihan 1

Biarkan vektor serentak, b dan c.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Tentukan vektor yang dihasilkan V_r = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3b = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_r = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_r = ([-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1))

V_r = (-15, -11, 17)

-Tentukan produk skalar (a . C)

(Kepada . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 -6 + 5

(Kepada . C) = 3

-Hitung sudut antara a dan c

(Kepada . C) = | a |.| C |.Cos θ di mana θ adalah sudut terpendek di kalangan vektor

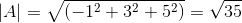
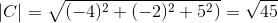
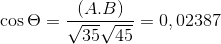
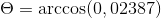
θ = 88.63⁰

 -Cari vektor tegak lurus ke a dan b

Untuk ini adalah perlu untuk menentukan produk vektor antara (-1, 3, 5) dan (3, 5, -2). Seperti yang dijelaskan sebelum ini, matriks 3 x 3 dibina di mana baris pertama terdiri daripada senarai vektor unit (i, j, k). Kemudian baris ke -2 dan ke -3 terdiri daripada vektor yang akan dikendalikan, menghormati pesanan operasi.

Boleh melayani anda: notasi perpuluhan

(A x b) = = [(-1) . 5 - (3 . 3)] Yo  - [(-1) . (-2) - (5 . 3)] J + [(-1) . 5 - (3 . 3)] k

(A x b) = (-5 - 9) Yo - (2 - 15) J + (-5 - 9) k         

(A x b) =  -14 i + 13 j - 14 k

Latihan 2 

Biarkan v_ke dan v_b Vektor halaju a dan b masing -masing. Kirakan kelajuan b dari a.

V_ke = (3, -1, 5) v_b = (2, 5, -3)

Dalam kes ini, kelajuan relatif B diminta dari V_B/a

V_B/a = V_B - V_Ke

V_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

Ini adalah vektor veloc B yang dilihat dari a. Di mana vektor baru kelajuan b diterangkan dengan merujuk pemerhati yang diposisikan dalam A dan bergerak dengan kelajuan a.

Latihan yang dicadangkan

1-Membina 3 vektor A, B dan C yang bersamaan dan mengaitkan 3 operasi di antara mereka melalui latihan praktikal.

2 -Vektor A: (-2, 4, -11), b: (1, -6, 9) dan c: (-2, -1, 10). Cari vektor tegak lurus ke: a dan b, c dan b, jumlah a + b + c.

4-vektor 3-Determine yang berserenjang antara satu sama lain, tanpa mengambil kira paksi koordinat.

5-menentukan kerja yang dilakukan oleh kekuatan yang mengangkat blok jisim 5 kg, dari bawah 20m dalam dengan baik.

Algebra 6-swamker bahawa pengurangan vektor adalah sama dengan jumlah vektor yang bertentangan. Membenarkan postulat anda.

7-Denote Vektor dalam semua notasi yang dibangunkan dalam artikel ini. (Cartesian, kutub, analisis dan sfera).

8-Daya magnet yang dikenakan pada magnet yang terletak di atas meja, diberikan oleh vektor berikut; V: (5, 3, -2), t: (4, 7, 9), h: (-3, 5, -4). Tentukan di mana arah magnet akan bergerak jika semua daya magnet bertindak pada masa yang sama.

Rujukan

1. Geometri dan Transforasi Euclidean. Clayton w. Dodge. Couer Corporation, 1 Jan. 2004
2. Cara menyelesaikan masalah matematik memohon l. Moiseiwitsch. Couer Corporation, 10 Apr. 2013
3. Konsep asas geometri. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4 Oktober. 2012
4. Vektor. Rocío Navarro Lacoba, 7 Jun. 2014
5. Algebra linear. Bernard Kolman, David R. Bukit. Pendidikan Pearson, 2006