Kelantangan

Kami menerangkan berapa kelantangan, formula, unit, bagaimana mengira dan memberikan beberapa contoh

Berapakah jumlahnya?

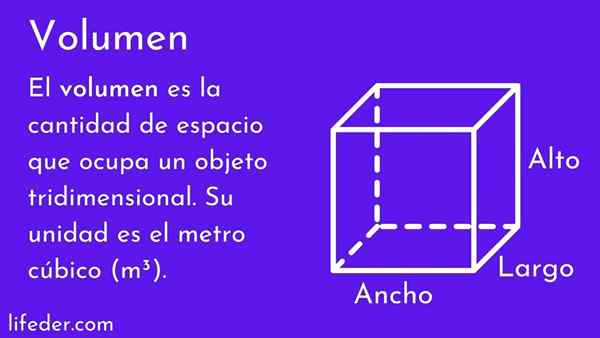
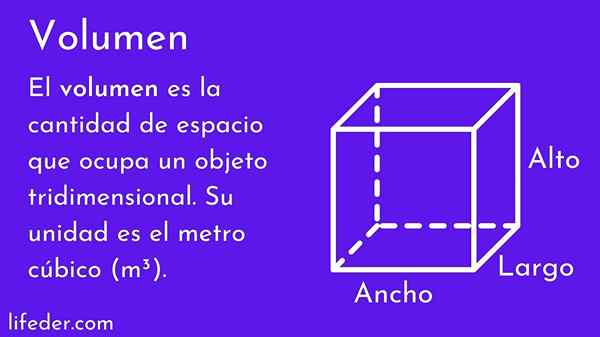
Dia kelantangan badan adalah nilai berangka yang mengukur jumlah ruang yang diduduki olehnya. Yang tinggi, lebar dan kedalaman menentukan kelantangan, semakin besar, semakin besar ruang yang diduduki.

Konsep kelantangan sangat penting, kerana dunia adalah tiga dimensi dan semua objek mempunyai lebar, ketinggian dan kedalaman, oleh itu mereka mempunyai kelantangan. Orang ramai menggunakannya dengan kerap, contohnya dengan menganggarkan sama ada perabot yang mereka mahu beli, ia sesuai di bilik mereka atau jika mereka memasuki saiz pakaian tertentu.

Di beberapa bidang sains dan kejuruteraan, seperti ketika bekerja dengan cecair, sama ada cecair atau gas, jumlah yang diduduki memperoleh sangat penting: apabila mengisi bekas dan mengepam cecair seperti air, atau dalam reka bentuk kapal untuk kapal untuk memastikan Anda tidak tenggelam. Semua ini menjadikannya penting untuk menentukannya untuk banyak proses.

Terdapat formula untuk mengira jumlah badan geometri dalam bentuk biasa, seperti prisma, sfera, silinder dan kon, sebagai contoh, bergantung kepada beberapa dimensinya. Dan ada juga cara untuk mengetahui jumlah objek yang tidak teratur, seperti yang akan diterangkan sedikit kemudian.

Formula kelantangan dalam angka geometri

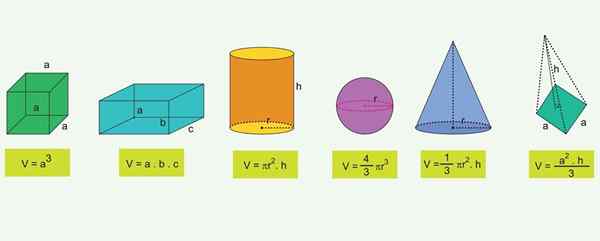Senarai angka geometri yang paling biasa dan formula jumlahnya

Untuk objek geometri yang paling terkenal terdapat formula yang membolehkan untuk mengira jumlahnya:

• Kiub

V = ℓ³ 

Di mana v mewakili kelantangan dan ℓ adalah kelebihan (sisi) kiub.

• Parallelepiped

Parallelepiped adalah kotak segi empat tepat dengan lebar "A", panjang ℓ dan "H" ketinggian. Jumlahnya diberikan oleh produk tiga dimensi:

V = A ∙ ℓ ∙ H

• Sfera

Jumlah sfera bergantung kepada jejari r:

Boleh melayani anda: Nicolás Copernico

• Silinder pekeliling lurus

Jumlah silinder bulat lurus adalah produk antara kawasan pangkalannya dan ketinggiannya "H". Sebagai pangkalannya adalah album radio "r", kawasannya adalah a = π · r², Jumlahnya kekal:

V = πr²∙ h

• Pussy

Jumlah kerucut adalah satu pertiga daripada produk antara kawasan asas bulat A dan ketinggian h. Seperti a = πr², Jadi:

• Piramid

Untuk piramid yang kawasan asasnya adalah dan mempunyai ketinggian "H", jumlahnya diberikan oleh:

Sekiranya piramid mempunyai asas persegi di sebelah "a", seperti dalam angka, kawasan asas pangkalan adalah untuk² Dan jumlah piramid adalah:

V = (1/3) ⋅A²⋅H

• Prisma

Jumlah prisma adalah produk antara kawasan asas A dan ketinggian "H":

V = A ∙ H

Unit volum

Dalam sistem unit antarabangsa, unit untuk kelantangan adalah meter padu atau m³, Semasa berada di sistem Anglo -saxon, ia adalah kaki padu atau ft³ (OF Kaki, yang dalam bahasa Inggeris bermaksud "kaki").

Terdapat banyak unit lain, mengikut saiz ruang yang diduduki. Contohnya, kilometer kubik km³ Untuk jumlah yang lebih besar atau milimeter padu mm³ Untuk jumlah kecil. Terdapat juga unit penggunaan tempatan.

Ia juga perlu menyebut unit kapasiti, berkait rapat dengan jumlah yang lebih baik digunakan untuk cecair. Unit kapasiti pusat adalah liter, disingkat L, yang bersamaan dengan DM³ (Decimeter padu).

Unit lain yang patut disebutkan adalah gelen, inci padu, cawan dan gout, yang terakhir digunakan untuk dos ubat.

Boleh melayani anda: kaedah perbandingan

Bagaimana jumlahnya diukur?

Jumlah badan, seperti ukuran lain, dijalankan dengan dibandingkan dengan corak yang mencukupi, dalam hal ini satu unit kelantangan.

Unit kelantangan ditakrifkan sebagai kiub yang kelebihannya mengukur 1 unit. Unit ini boleh menjadi meter, sentimeter, kaki, inci atau yang lain. Kemudian, kelantangan objek sepadan dengan jumlah unit padu yang diduduki oleh angka dan selalu jumlah positif.

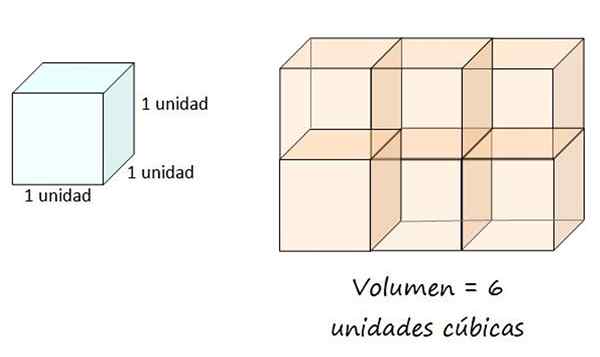Unit padu ditakrifkan sebagai kelantangan baldi dengan tepi sama dengan 1, jadi kotak di sebelah kanan mempunyai isipadu 6 unit padu. Sumber: f. Zapata.

Kelantangan badan geometri

Ketika datang ke badan geometri seperti yang telah disebutkan, jumlahnya dikira melalui formula yang sesuai, mengukur dimensi yang ditunjukkan oleh formula.

Sebagai contoh, jika anda ingin mengetahui jumlah sfera, perlu mengukur diameternya dan dengan itu jejanya diketahui, iaitu separuh. Sekiranya ia adalah kotak segi empat tepat, lebar, ketinggian dan kedalaman yang sama diukur.

Kemudian nilai -nilai yang diminta dalam formula dimasukkan, menjaga semua unit adalah sama, operasi yang diperlukan dijalankan, ada jumlah objek.

Kelantangan badan yang tidak teratur

Pepejal yang tidak teratur tidak mempunyai bentuk geometri, seperti batu atau wink. Walaupun demikian, anda dapat menemui kelantangannya dengan bantuan bekas lulus yang penuh dengan air, melalui kaedah perpindahan cecair.

Pada mulanya, jumlah yang diduduki oleh air ditentukan dan kemudian objek tidak teratur sepenuhnya direndam, mengukur jumlah baru, yang lebih besar daripada yang asal. Jumlah objek yang tidak teratur adalah perbezaan antara jumlah ini dan air sahaja.

Boleh melayani anda: Genie Wiley, gadis liar yang hanya mengenali namanya

Agar kaedah ini berfungsi, objek tidak boleh dibuat dari apa -apa bahan yang mudah dibubarkan di dalam air, ia mesti tetap tenggelam sepenuhnya dan tentu saja, anda perlu mempunyai bekas lulus saiz yang diperlukan untuk menampungnya sepenuhnya.

Contoh kelantangan

Jumlah anggaran beberapa objek yang diketahui ialah:

• Bumi: 1.08321 × 10¹² km³
• Sungai Amazonas: 225.000 m³/s (jumlah per unit masa dipanggil "aliran")
• Piramid Hebat Giza: 2.600.000 m³
• Bola sepak: 5600 cm³
• Beg galas: 50 dm³

Jilid dan Massa

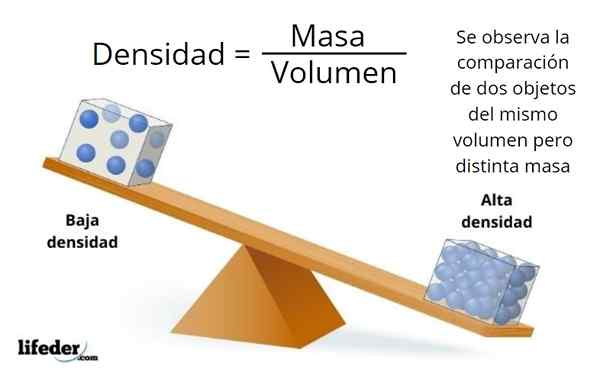
Jumlah dan jisim bukan sinonim, yang pertama dikaitkan dengan dimensi objek dan yang kedua dengan jumlah perkara yang terkandung di dalamnya.

Mungkin terdapat banyak perkara dalam objek dimensi kecil, atau sangat sedikit dalam objek besar, yang bergantung kepada ketumpatan bahan, yang merupakan nisbah antara jisim dan jumlah objek:

Latihan yang diselesaikan

Latihan 1

Kirakan kelantangan kotak segi empat tepat yang dimensi 34 cm × 22 cm × 8 cm.

• Penyelesaian

Jumlah kotak segi empat tepat hanyalah produk tiga dimensi:

V = 34 cm × 22 cm × 8 cm = 5984 cm³

Latihan 2

Pangkalan piramid kuadrangular mempunyai kawasan seluas 16 cm² Dan ketinggiannya adalah 6 cm. Kirakan jumlah piramid tersebut.

• Penyelesaian

Formula yang diberikan di atas untuk jumlah piramid digunakan, diketahui kawasan pangkalannya:

Dan nilai berangka diganti:

V = (1/3) × 16 cm² × 6 cm = 32 cm³