Definisi Percepatan Centripetal, Formula, Pengiraan, Latihan

The pecutan centripetal ke_c, Juga dipanggil jejari atau normal, ia adalah pecutan yang membawa objek mudah alih ketika menerangkan trajektori bulat. Magnitudnya v²/r, di mana r Ia adalah jejari bulatan, ia diarahkan ke pusatnya dan bertanggungjawab untuk mudah alih untuk kekal dalam laluannya.

Dimensi pecutan sentripetal panjang per unit waktu. Dalam sistem antarabangsa mereka adalah m/s². Sekiranya atas sebab tertentu pecutan sentripetus hilang, begitu juga kekuatan yang memaksa mudah alih untuk mengekalkan trajektori bulat.

Objek pusingan mempunyai pecutan sentripetal, yang diarahkan ke pusat trajektori. Sumber: Pixabay

Inilah yang berlaku pada kereta yang cuba memberikan lengkung di trek rata dan fros, di mana geseran di antara lantai dan roda tidak mencukupi supaya kereta mengambil lengkung. Oleh itu satu -satunya kemungkinan yang anda tinggalkan adalah bergerak dalam garis lurus dan itulah sebabnya anda keluar dari lengkung.

[TOC]

Pergerakan bulat

Apabila objek bergerak dalam bulatan, pada setiap masa pecutan sentripetal diarahkan ke arah pusat lilitan, arah yang berserenjang dengan trajektori diikuti.

Oleh kerana kelajuan selalu tangen dengan trajektori, jadi kelajuan dan percepatan sentripetal berubah menjadi tegak lurus. Oleh itu kelajuan dan pecutan tidak selalu mempunyai arah yang sama.

Dalam keadaan ini, mudah alih mempunyai kemungkinan menggambarkan lilitan dengan kelajuan yang tetap atau berubah -ubah. Kes pertama dikenali sebagai Pergerakan Pekeliling Seragam atau MCU oleh akronimnya, kes kedua akan menjadi pergerakan bulat berubah -ubah.

Ia dapat melayani anda: apakah pelepasan pelepasan? (Dengan contoh)

Dalam kedua -dua kes, pecutan sentripetal bertanggungjawab untuk menjaga keliling mudah alih, menduduki bahawa kelajuan hanya berbeza ke arah dan arah.

Walau bagaimanapun, untuk mempunyai pergerakan bulat yang berubah -ubah, komponen percepatan lain dalam arah yang sama kelajuan diperlukan, yang bertanggungjawab untuk meningkatkan atau menurunkan kelajuan. Komponen pecutan ini dikenali sebagai Pecutan tangen.

Pergerakan pekeliling yang berubah -ubah dan pergerakan curvilinear pada umum.

Pasukan sentripetal

Sekarang, kekuatan bertanggungjawab untuk memberikan pecutan. Untuk satelit yang mengorbit bumi, ia adalah kekuatan graviti. Dan kerana graviti selalu bertindak tegak lurus dengan trajektori, ia tidak mengubah kelajuan satelit.

Dalam kes ini, graviti bertindak sebagai Kekuatan Centripetal, Bahawa ia bukan kelas khas atau selain dari kekerasan, tetapi satu yang dalam hal satelit, secara radiasi diarahkan ke pusat bumi.

Dalam jenis pergerakan bulat lain, contohnya kereta yang mengambil lengkung, peranan daya sentripet ditafsirkan oleh daya rubb statik yang memaksa mudah alih untuk beralih.

Formula untuk pecutan sentripetal

Percepatan sentripetal dikira dengan ungkapan:

Ac = v²/r

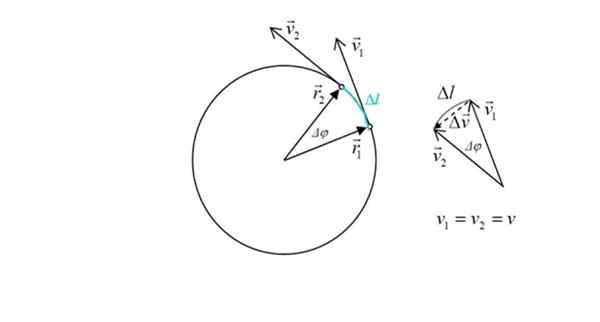
Rajah untuk mengira pecutan sentripetal dalam telefon bimbit dengan MCU. Sumber: Sumber: Ilevanat [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Ungkapan ini akan disimpulkan di bawah. Dengan pecutan definisi adalah variasi kelajuan dalam masa:

Ia boleh melayani anda: sumber cahaya: jenis dan peranti yang memancarkan cahaya

Rajah teratas ditunjukkan di angka kiri, dua mata di mana lulus mudah alih yang bergerak di lingkaran radio r Dalam rasa antihorarium. Perhatikan bahawa magnitud kelajuan adalah sama dalam kedua -dua kes, tetapi bukan arah atau makna.

Mudah alih menggunakan masa δt Dalam lawatan, yang kecil, kerana mata sangat dekat.

Angka ini juga menunjukkan dua vektor kedudukan r₁ dan r₂, Modul yang sama: radio r dari lilitan. Sudut antara kedua -dua titik adalah Δφ. Dalam hijau tunduk Lawatan mudah alih, dilambangkan sebagai ΔL.

Dalam angka di sebelah kanan dilihat bahawa magnitud δv, Perubahan kelajuan adalah kira -kira berkadar dengan ΔL, kerana sudut Δφ adalah kecil. Tetapi perubahan kelajuan berkaitan dengan pecutan. Segitiga diberi amaran, dengan jumlah vektor yang:

v₁ + Δv = v₂ → δV = V₂ - v₁

Δv Ia menarik, kerana ia berkadar dengan pecutan sentripetal. Dari angka itu diberi amaran bahawa menjadi sudut kecil Δφ, vektor δv Ia berada dalam intipati tegak lurus kedua -duanya v₁ Seperti v₂ dan menunjuk ke pusat lilitan.

Walaupun vektor menonjol dengan berani, untuk kesan sifat geometri yang mengikuti, kami bekerja dengan modul atau magnitud vektor ini, tanpa mengira notasi vektor.

Sesuatu yang lain: anda perlu menggunakan definisi sudut pusat, iaitu:

Δφ= Δl/r

Sekarang kedua -dua angka dibandingkan, yang berkadar sejak sudut δφ ia biasa:

Boleh melayani anda: Apakah cahaya terpolarisasi?

 

Membahagikan antara ΔT:

 Kerana dengan definisi kelajuan ialah V = ΔL/ ΔT. Tetapi δV/ Δt Ia adalah tepatnya magnitud pecutan sentripetal, yang mana yang dicari. Dengan cara ini ungkapan yang diterangkan pada mulanya dicapai:

ke_c= v²/r

Latihan diselesaikan

Zarah bergerak dalam lingkaran 2.70 m Radio. Pada masa tertentu pecutannya adalah 1.05 m/s² Ke arah yang menjadikan sudut 32.0º dengan Direktorat Pergerakan. Kirakan kelajuan anda:

a) Pada masa itu

b) 2.00 saat kemudian, dengan mengandaikan pecutan tangen yang berterusan.

Jawapan

Ia adalah pergerakan pekeliling yang bervariasi, kerana pernyataan menunjukkan bahawa pecutan mempunyai sudut yang diberikan dengan arah pergerakan yang tidak atau 0º (ia tidak boleh menjadi pergerakan bulat) atau 90º (ia akan menjadi pergerakan pekeliling seragam).

Oleh itu, kedua -dua komponen - radial dan tangen - wujud bersama. Akan dilambangkan sebagai_c sudah_t dan kelihatan ditarik dalam angka berikut. Vektor hijau adalah vektor pecutan bersih atau hanya pecutan ke.

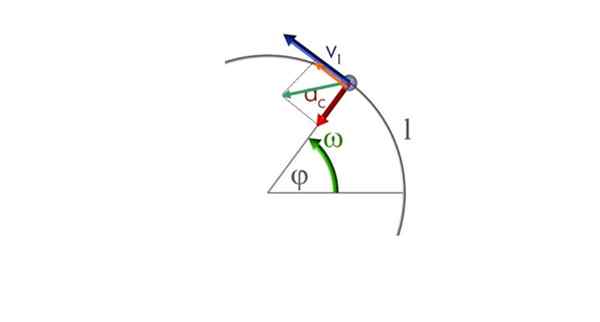Zarah bergerak dalam trajektori bulat dalam erti kata antihorary dan pergerakan bulat yang bervariasi. Sumber: Commons.Wikimedia.org

a) Pengiraan komponen pecutan

ke_c = a.cos θ = 1.05 m/s² . cos 32.0º = 0.89 m/s² (dalam merah)

ke_t = a.dosa θ = 1.05 m/s² . Sen 32.0º = 0.57 m/s² (dalam oren)

Pengiraan kelajuan mudah alih

Sejak a_c = v²/r, Jadi:
b) 2 saat kemudian kelajuan v akan meningkat terima kasih kepada komponen pecutan tangen

V = V_{Sama ada} +ke_t. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Rujukan

1. Giancoli, d. Fizik. 2006. Prinsip dengan aplikasi. Edisi keenam. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Sains Fizikal Konsep. Edisi Kelima.Pearson.106 - 108.