Formula dan persamaan antiderivatif, contoh, latihan

A antiderivatif F (x) fungsi F(x) juga dipanggil primitif atau hanya integral fungsi yang tidak terbatas, jika dalam selang waktu tertentu Yo, Memang benar bahawa F '(x) = f (x)

Sebagai contoh, mari kita ambil fungsi berikut:

f (x) = 4x³

Antiderivatif fungsi ini ialah f (x) = x⁴, kerana dengan memperoleh f (x) oleh peraturan derivasi untuk kuasa:

Ia diperoleh dengan tepat f (x) = 4x³.

Walau bagaimanapun, ini hanya salah satu daripada banyak antiderivatif f (x), kerana fungsi lain ini: g (x) = x⁴ + 2 Ia juga, kerana dengan memperoleh g (x) berkenaan dengan x, ia adalah sama diperolehi kembali f (x).

Mari kita periksa:

Ingat bahawa yang berasal dari pemalar adalah 0. Oleh itu kepada istilah x⁴ Anda boleh menambah sebarang pemalar dan derivatifnya akan terus menjadi 4x³.

Disimpulkan bahawa sebarang fungsi bentuk umum f (x) = x⁴ + C, di mana C adalah pemalar sebenar, berfungsi sebagai antiderivatif f (x).

Contoh ilustrasi terdahulu boleh dinyatakan seperti berikut:

df (x) = 4x³ Dx

Antiderivatif atau integral yang tidak ditentukan dinyatakan dengan simbol ∫, oleh itu:

F (x) = ∫4x³ dx = x⁴ + C

Di mana fungsi f (x) = 4x³  Ia dikenali sebagai mengintegrasikan, dan c adalah Pemalar integrasi.

[TOC]

Contoh antiderivatif

Rajah 1. Anti -hotley tidak lebih dari sekadar integral. Sumber: Pixabay.

Mencari antiderivatif fungsi adalah mudah dalam beberapa kes di mana derivatif terkenal. Sebagai contoh, menjadi fungsi f (x) = sen x, yang tidak disatukan kerana ia adalah fungsi lain f (x), sehingga apabila diperolehnya diperoleh f (x).

Fungsi itu boleh:

F (x) = - cos x

Mari kita periksa bahawa itu benar:

F '(x) = (- cos x)' =- (-sen x) = sin x

Oleh itu kita boleh menulis:

∫sen x dx = -cos x + c

Di samping mengetahui derivatif, terdapat peraturan integrasi asas dan mudah untuk mencari antiderivatif atau integral yang tidak terbatas.

Boleh melayani anda: derivatif berturut -turut

Jadilah pemalar sebenar, maka:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Sekiranya fungsi H (x) boleh dinyatakan sebagai jumlah atau penolakan dua fungsi, maka integralnya tidak terbatas adalah:

3.- ∫H (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Ini adalah hak milik linearity.

The Peraturan kuasa Untuk integral ia boleh ditubuhkan dengan cara ini:

Peraturan ini mempunyai sekatan yang jelas: sejak penyebut N +1 Ia tidak dapat dilakukan 0, oleh itu n ≠ -1.

Dalam kes n = -1 peraturan berikut digunakan:

5.- ∫x ^-1 Dx = ln x +c

Mudah untuk menunjukkan bahawa terbitan ln x ia adalah tepat x ^-1.

Persamaan pembezaan

Persamaan pembezaan adalah satu di mana yang tidak diketahui adalah sebagai derivatif.

Sekarang, dari analisis sebelumnya, mudah untuk menyedari bahawa operasi songsang ke derivatif adalah antiderivatif yang tidak ditentukan atau integral.

Biarkan f (x) = y '(x), iaitu, berasal dari fungsi tertentu. Kita boleh menggunakan notasi berikut untuk menunjukkan derivatif ini:

Ia segera mengikutinya:

dy = f (x) dx

Yang tidak diketahui persamaan pembezaan adalah fungsi y (x), yang derivatifnya adalah f (x). Untuk membersihkannya, ungkapan sebelumnya disepadukan di kedua -dua belah pihak, yang bersamaan dengan menggunakan antiderivatif:

∫dy = ∫f (x) dx

Integral kiri diselesaikan oleh Peraturan Integrasi 1, dengan K = 1 dan oleh itu yang dicari -Awaite dibersihkan:

dan (x) = ∫f (x) dx = f (x) + c

Dan kerana C adalah pemalar sebenar, untuk mengetahui yang sesuai dalam setiap kes, pernyataan mesti mengandungi maklumat tambahan yang mencukupi untuk mengira nilai c. Ini dipanggil Keadaan awal.

Kami akan melihat contoh permohonan semua ini di bahagian seterusnya.

Boleh melayani anda: anggaran tepat waktu

Latihan Antiderivated

- Latihan 1

Gunakan peraturan integrasi untuk mendapatkan antiderivatif yang tidak ditentukan atau integral fungsi yang diberikan, memudahkan hasil sebanyak mungkin. Adalah mudah untuk mengesahkan hasilnya dengan terbitan.

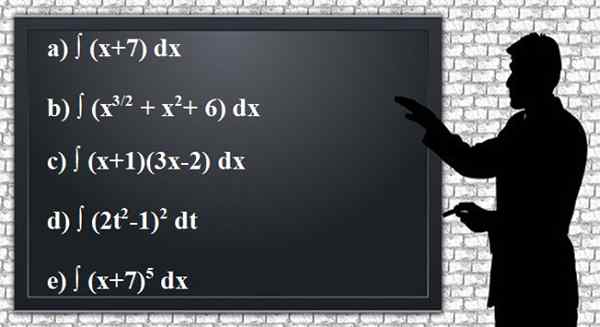Rajah 2. Latihan anterivasi atau integral yang ditakrifkan. Sumber: Pixabay.

Penyelesaian kepada

Kami mula -mula memohon Peraturan 3, kerana pengintegrasian adalah jumlah dua istilah:

∫ (x +7) dx = ∫ xdx +∫7dx

Untuk integral pertama peraturan kuasa digunakan:

∫ xdx = (x² /2)+c₁

Dalam Peraturan Integral Kedua 1 terpakai, iaitu k = 7:

∫7dx = 7∫dx = 7x + c₂

Dan sekarang hasilnya ditambah. Kedua -dua pemalar dikelompokkan menjadi satu, secara umumnya dipanggil C:

∫ (x+7) dx = (x² /2) + 7x + c

Penyelesaian b

Dengan linearity ini terurai integral menjadi tiga integral yang lebih mudah, yang mana peraturan kuasa akan digunakan:

∫ (x^3/2 + x² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Perhatikan bahawa bagi setiap integral, pemalar integrasi muncul, tetapi mereka bertemu dalam satu panggilan c.

Penyelesaian c

Dalam kes ini, adalah mudah untuk memohon harta pengedaran pendaraban untuk membangunkan pengintegrasian. Kemudian anda menggunakan peraturan kuasa untuk mencari setiap integral secara berasingan, seperti pada tahun sebelumnya.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Pembaca yang penuh perhatian akan memerhatikan bahawa kedua -dua istilah utama adalah sama, oleh itu mereka dikurangkan sebelum mengintegrasikan:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Penyelesaian e

Cara untuk menyelesaikan integral adalah untuk membangunkan kuasa, seperti yang dilakukan dalam Contoh D. Walau bagaimanapun, kerana eksponen lebih tinggi, perlu membuat perubahan berubah -ubah, supaya tidak perlu membuat perkembangan yang panjang.

Boleh melayani anda: Pemboleh ubah rawak berterusan

Perubahan berubah adalah seperti berikut:

U = x + 7

Memperoleh kedua -dua pihak ungkapan ini:

du = dx

Integral berubah menjadi lebih mudah dengan pemboleh ubah baru, yang diselesaikan dengan peraturan kuasa:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Akhirnya, perubahan itu dikembalikan untuk kembali ke pemboleh ubah asal:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Latihan 2

Zarah pada mulanya berehat dan bergerak di sepanjang paksi x. Pecutannya untuk t> 0 diberikan oleh fungsi a (t) = cos t. Adalah diketahui bahawa pada t = 0, kedudukannya adalah x = 3, semuanya dalam unit sistem antarabangsa. Diminta untuk mencari kelajuan v (t) dan kedudukan x (t) zarah.

Penyelesaian

Oleh kerana pecutan adalah yang pertama diperoleh dari kelajuan berkenaan dengan masa, anda mempunyai persamaan pembezaan berikut:

a (t) = v '(t) = cos t

Ia mengikutinya:

v (t) = ∫ cos t dt = sin t + c₁

Sebaliknya, kita tahu bahawa kelajuan adalah seterusnya terbitan kedudukan, oleh itu kita mengintegrasikan semula:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Pemalar integrasi ditentukan dari maklumat yang diberikan dalam pernyataan. Pertama, dia mengatakan bahawa zarah pada mulanya berehat, oleh itu V (0) = 0:

V (0) = dosa 0 + c₁ = 0

C₁ = 0

Maka anda perlu x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + c₂ = 3 → C₂ = 3+1 = 4

Fungsi kelajuan dan kedudukan pasti seperti ini:

v (t) = sen t

x (t) = - cos t + 4

Rujukan

1. Engler, a. 2019. Kalkulus integral. Universiti Kebangsaan Pantai.
2. Larson, r. 2010. Pengiraan pemboleh ubah. 9NA. Edisi. McGraw Hill.
3. Teks matematik percuma. Antiderivatif. Pulih dari: matematik.Liibretexts.org.
4. Wikipedia. Antiderivatif. Diperoleh dari: dalam.Wikipedia.org.
5. Wikipedia. Integrasi tidak terbatas. Pulih dari: Adakah.Wikipedia.org.