Pengagihan Chi-square (χ²), bagaimana ia dikira, contohnya

Bukti Chi Squared Sama ada ji-square (χ², Di mana χ adalah huruf Yunani yang dipanggil "chi") digunakan untuk menentukan tingkah laku pembolehubah tertentu dan juga apabila anda ingin mengetahui sama ada dua atau lebih pembolehubah secara statistik bebas.

Untuk memeriksa tingkah laku pemboleh ubah, ujian yang akan dipanggil Ujian penyesuaian chi persegi. Untuk mengetahui sama ada dua atau lebih pembolehubah secara statistik bebas daripada ujian dipanggil Chi Square of Kemerdekaan, juga dipanggil kontingensi.

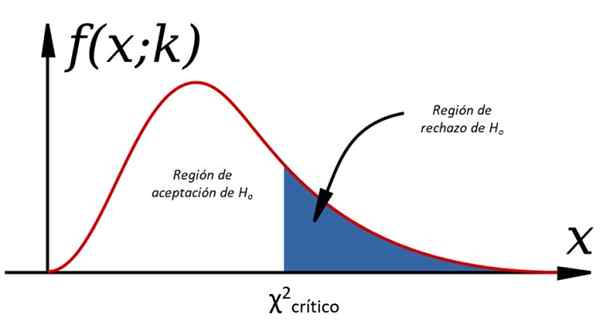
Rajah 1. Ujian Hipotesis melalui Chi Cuadrado

Bukti ini adalah sebahagian daripada teori statistik keputusan, di mana populasi dikaji dan keputusan dibuat mengenainya, menganalisis satu atau beberapa sampel yang diekstrak daripadanya. Untuk ini adalah perlu untuk membuat andaian tertentu mengenai pembolehubah, yang dipanggil hipotesis, yang mungkin atau mungkin tidak pasti.

Terdapat beberapa ujian untuk membezakan ramalan ini dan menentukan yang sah, dalam margin keyakinan tertentu, termasuk ujian chi-square, yang boleh digunakan untuk membandingkan dua dan kebanyakan populasi.

Seperti yang akan kita lihat, dua jenis hipotesis mengenai beberapa parameter populasi dalam dua sampel biasanya dipertimbangkan: hipotesis nol, yang dipanggil h_{Sama ada} (Sampel adalah bebas), dan hipotesis alternatif, dilambangkan sebagai h₁, (sampel berkorelasi) yang bertentangan dengan itu.

[TOC]

Bilakah ujian chi-square digunakan?

Ujian Chi Square terpakai kepada pembolehubah yang menggambarkan kualiti, seperti seks, status sivil, kumpulan darah, warna mata dan keutamaan pelbagai jenis.

Ujian ini direka apabila dikehendaki:

-Periksa sama ada pengedaran sesuai untuk menggambarkan pembolehubah, yang dipanggil kebaikan pelarasan. Melalui ujian Square Chi, anda dapat mengetahui jika terdapat perbezaan yang signifikan antara taburan teoritis yang dipilih dan pengagihan kekerapan diperhatikan.

-Ketahui jika pembolehubah dua x dan y bebas dari sudut pandang statistik. Ini dikenali sebagai Ujian Kemerdekaan.

Oleh kerana ia terpakai kepada pembolehubah kualitatif atau kategori, ujian Square Chi digunakan secara meluas dalam sains sosial, pentadbiran dan perubatan.

Syarat untuk menerapkannya

Terdapat dua keperluan penting untuk menerapkannya dengan betul:

Ia dapat melayani anda: apakah hubungan antara kawasan rhombus dan segi empat tepat?

-Data mesti dikumpulkan dalam frekuensi.

-Sampel mesti cukup besar untuk menjadikan pengedaran Chi Square sah, jika tidak, nilainya dipandang terlalu banyak dan menimbulkan penolakan hipotesis nol apabila tidak sepatutnya.

Peraturan umum ialah jika dalam data dikumpulkan kekerapan dengan nilai kurang daripada 5 muncul, ia tidak digunakan. Sekiranya terdapat lebih daripada satu kekerapan kurang daripada 5, maka mereka mesti digabungkan dalam satu untuk mendapatkan kekerapan dengan nilai berangka lebih besar daripada 5.

Pengagihan Square Chi

χ² Ia adalah pengagihan kebarangkalian berterusan. Sebenarnya ada lengkung yang berbeza, bergantung pada parameter k dipanggil darjah kebebasan secara rawak.

Sifatnya adalah:

-Kawasan di bawah lengkungnya sama dengan 1.

-Nilai χ² Mereka positif.

-Pengagihan tidak simetris, iaitu, ia mempunyai kecenderungan.

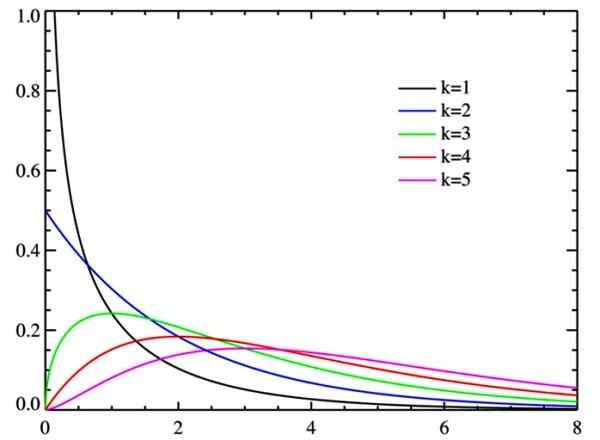Rajah 2. Pengagihan Chi Square untuk Watts Darjah Kebebasan. Sumber: Wikimedia Commons.

Darjah kebebasan

Apabila tahap kebebasan meningkat, pengedaran chi-square cenderung normal, seperti yang dapat dilihat dalam angka.

Untuk pengedaran yang diberikan, darjah kebebasan ditentukan melalui Jadual kontingensi, yang merupakan jadual di mana frekuensi yang diperhatikan dari pembolehubah dicatatkan.

Sekiranya jadual mempunyai F pangkat dan c lajur, nilai k adalah:

K = (f - 1) ⋅ (c - 1)

Perumusan hipotesis

Apabila ujian Square Chi adalah pelarasan, hipotesis berikut dirumuskan:

-H_{Sama ada}: Variabel x mempunyai taburan kebarangkalian f (x) dengan parameter tertentu dan₁, dan₂..., dan_p

-H₁: X mempunyai taburan kebarangkalian lain.

Pengagihan kebarangkalian yang diandaikan dalam hipotesis nol boleh, contohnya, pengedaran normal yang terkenal, dan parameternya akan menjadi purata μ dan sisihan piawai σ.

Di samping itu, hipotesis nol dinilai dengan tahap kepentingan tertentu, iaitu ukuran kesilapan yang akan dibuat apabila menolaknya menjadi benar.

Secara umum, tahap ini ditubuhkan sebanyak 1 %, 5 % atau 10 % dan semakin rendah hasil ujian, semakin dipercayai.

Boleh melayani anda: mumm

Dan jika ujian kontingensi Chi Square digunakan, yang seperti yang kita katakan berfungsi untuk mengesahkan kebebasan antara dua pembolehubah x dan y, hipotesis adalah:

-H_{Sama ada}: Pembolehubah x dan y adalah bebas.

-H₁: X dan y bergantung.

Sekali lagi adalah perlu untuk menentukan tahap kepentingan untuk mengetahui ukuran kesilapan ketika membuat keputusan.

Bagaimana statistik chi-square dikira?

Statistik Chi Square dikira seperti berikut:

Simbol Σ bermaksud "penjumlahan", yang mesti kita buat mengenai ungkapan pecahan yang ditunjukkan.

Jumlahnya dijalankan dari kelas pertama I = 1 hingga yang terakhir, iaitu i = k.

Selain:

-F_{Sama ada} Ia adalah kekerapan yang diperhatikan (ia berasal dari data yang diperoleh).

-F_dan Ia adalah kekerapan yang diharapkan atau teoritis (perlu mengira dari data).

Untuk menerima atau menolak hipotesis nol, χ dikira² Untuk data yang diperhatikan dan dibandingkan dengan nilai yang dipanggil Chi Critical Square, yang bergantung pada tahap kebebasan k dan tahap kepentingan α:

χ²_kritikal =  χ²_{K, α}

Jika, sebagai contoh, kami mahu melakukan ujian dengan tahap penting 1 %, maka α = 0.01, jika akan dengan 5% maka α = 0.05 dan sebagainya. P, parameter pengedaran, seperti:

P = 1 - α

Nilai persegi kritikal ini ditentukan oleh jadual yang mengandungi nilai kawasan terkumpul. Sebagai contoh, untuk k = 1, yang mewakili 1 darjah kebebasan dan α = 0.05, bersamaan dengan p = 1-.05 = 0.95, nilai χ² Ia adalah 3.841.

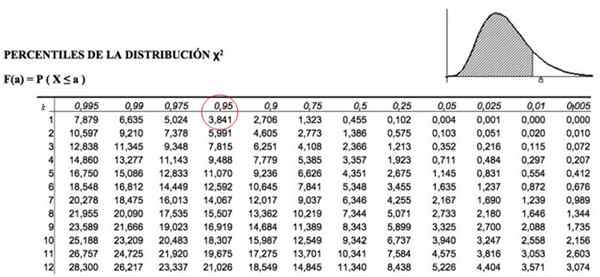Rajah 3. Jadual Nilai Pengedaran Chi Square. Sumber: f. Zapata.

Kriteria Penerimaan AC_{Sama ada}

Kriteria untuk menerima h_{Sama ada} adalah:

-Ya χ² < χ²_kritikal  H_{Sama ada}, jika tidak, ia ditolak (lihat Rajah 1).

Contoh pengiraan

Dalam permohonan berikut ujian Chi Square akan digunakan sebagai ujian kemerdekaan.

Anggapkan bahawa penyelidik ingin mengetahui sama ada keutamaan untuk kopi hitam berkaitan dengan genre seseorang, dan nyatakan jawapannya dengan tahap kepentingan α = 0.05.

Boleh melayani anda: Sudut alternatif luaran: Latihan dan Latihan Diselesaikan

Untuk ini, sampel 100 orang yang ditemuramah dan jawapan mereka boleh didapati:

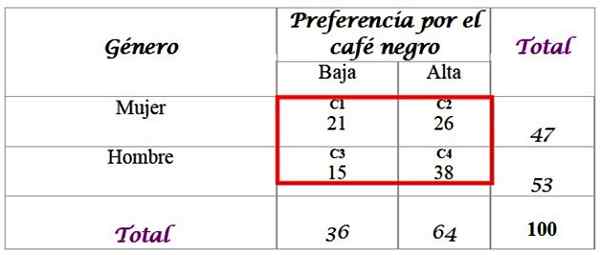
Langkah 1

Mewujudkan hipotesis:

-H_{Sama ada}: jantina dan keutamaan untuk kopi hitam bebas.
-H₁: Rasa kopi hitam berkaitan dengan genre seseorang.

Langkah 2

Kirakan frekuensi yang dijangkakan untuk pengedaran, yang mana jumlahnya ditambah pada baris terakhir dan di lajur kanan -wing diperlukan. Setiap sel di kotak merah mempunyai nilai yang diharapkan F_dan, yang dikira dengan mendarabkan jumlah barinya F dengan jumlah lajur C, dibahagikan dengan jumlah sampel n:

F_dan = (F x c) /n

Hasilnya adalah seperti berikut untuk setiap sel:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Langkah 3

Kemudian anda perlu mengira statistik Chi Cuadrado untuk pengedaran ini, mengikut formula yang diberikan:

χ²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Langkah 4

Tentukan χ²_kritikal, Mengetahui bahawa data berdaftar berada di f = 2 baris dan c = 2 lajur, oleh itu, bilangan darjah kebebasan adalah:

K = (2-1) ⋅ (2-1) = 1.

Yang bermaksud bahawa kita mesti melihat dalam jadual yang ditunjukkan di atas nilai χ²_{K, α} = χ²_{1; 0.05} , iaitu:

χ²_kritikal = 3.841

Langkah 5

Bandingkan nilai dan tentukan:

χ² = 2.9005

χ²_kritikal = 3.841

Sejak χ² < χ²_kritikal Hipotesis nol diterima dan disimpulkan bahawa keutamaan untuk kopi hitam tidak dikaitkan dengan genre seseorang, dengan tahap kepentingan 5%.

Rujukan

1. Ujian Chi Square untuk Kemerdekaan. Pulih dari: Saylordotorg.Github.Io.
2. Gelombang med. Statistik yang digunakan untuk sains kesihatan: ujian ji-square. Pulih dari: medwave.Cl.
3. Kebarangkalian dan statistik. Ujian kebaikan pelarasan shi persegi. Diperolehi daripada: Kebarangkalian Andestik.com.
4. Triola, m. 2012. Statistik asas. 11hb. Edisi. Addison Wesley.
5. Unam. Ujian Square Chi. Pulih dari: nasihat.CUAutitlan2.Unam.mx.