Contoh data dikumpulkan dan latihan yang diselesaikan

The Data dikumpulkan Mereka adalah mereka yang telah diklasifikasikan ke dalam kategori atau kelas, mengambil kriteria kekerapan mereka. Ini dilakukan dengan tujuan memudahkan pengurusan data yang banyak dan mewujudkan trend mereka.

Setelah dianjurkan dalam kelas ini untuk frekuensi mereka, data membuat a Pengagihan kekerapan, dari mana maklumat utiliti diekstrak melalui ciri -cirinya.

Rajah 1. Dengan data dikumpulkan, anda boleh membina grafik dan mengira parameter statistik yang menggambarkan trend. Sumber: Pixabay.

Seterusnya kita akan melihat contoh mudah data dikumpulkan:

Katakan kedudukan 100 pelajar wanita, yang dipilih dari kalangan semua kursus fizik asas universiti, diukur dan hasil berikut diperoleh:

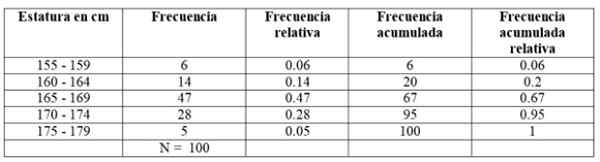
Keputusan yang diperoleh dibahagikan kepada 5 kelas, yang muncul di lajur kiri.

Kelas pertama, antara 155 dan 159 cm, mempunyai 6 pelajar, kelas kedua 160 - 164 cm mempunyai 14 pelajar, kelas ketiga dari 165 hingga 169 cm adalah yang mempunyai jumlah ahli terbesar: 47. Kemudian ikuti kelas 170-174 cm dengan 28 pelajar dan akhirnya dari 175 hingga 179 cm dengan hanya 5.

Bilangan ahli setiap kelas adalah tepat kekerapan Sama ada Frekuensi mutlak Dan dengan menambahkan semuanya, jumlah data diperoleh, yang dalam contoh ini adalah 100.

[TOC]

Ciri -ciri pengagihan kekerapan

Kekerapan

Seperti yang telah kita lihat, kekerapan adalah bilangan kali fakta diulang. Dan untuk memudahkan pengiraan sifat pengedaran, seperti purata dan varians, kuantiti berikut ditakrifkan:

-Kekerapan terkumpul: Ia diperoleh dengan menambahkan kekerapan kelas dengan kekerapan terkumpul anterior. Yang pertama dari semua frekuensi bertepatan dengan selang waktu yang dipersoalkan, dan yang terakhir adalah jumlah data.

-Frekuensi relatif: Ia dikira dengan membahagikan kekerapan mutlak setiap kelas dengan jumlah data. Dan jika mendarabkan sebanyak 100 anda mempunyai peratusan frekuensi peratusan.

Boleh melayani anda: fungsi vektor

-Kekerapan relatif terkumpul: Itu adalah jumlah frekuensi relatif setiap kelas dengan yang terkumpul sebelumnya. Yang terakhir dari frekuensi relatif terkumpul mestilah sama dengan 1.

Sebagai contoh, frekuensi seperti ini:

Sempadan

Nilai melampau setiap kelas atau selang dipanggil Had kelas. Seperti yang dapat kita lihat, setiap kelas mempunyai had yang lebih rendah dan lebih besar. Sebagai contoh, kelas pertama kajian mengenai statur mempunyai had kurang daripada 155 cm dan satu lebih besar daripada 159 cm.

Contoh ini mempunyai had yang jelas ditakrifkan, namun mungkin.

Sempadan

Ketinggian adalah pemboleh ubah berterusan, jadi dapat dipertimbangkan bahawa kelas pertama sebenarnya bermula pada tahun 154.5 cm, kerana dengan bulat nilai ini ke integer terdekat, 155 cm diperoleh.

Kelas ini merangkumi semua nilai sehingga 159.5 cm, kerana dari ini, statur dibulatkan hingga 160.0 cm. Kedudukan 159.7 cm sudah milik kelas seterusnya.

Sempadan kelas sebenar contoh ini adalah, dalam cm:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplitud

Keluasan kelas diperoleh dengan menolak sempadan. Untuk selang pertama contoh kami, anda mempunyai 159.5 - 154.5 cm = 5 cm.

Pembaca boleh mengesahkan bahawa untuk selang masa lain contoh amplitud juga hasil dari 5 cm. Walau bagaimanapun, perlu diperhatikan bahawa pengagihan boleh dibina dengan selang amplitud yang berbeza.

Ia boleh melayani anda: Peraturan T: Ciri -ciri, supaya ia, contohnya

Jenama Kelas

Ia adalah titik sederhana selang dan diperoleh dengan purata antara had atas dan had bawah.

Sebagai contoh, jenama kelas pertama ialah (155 + 159)/2 = 157 cm. Pembaca boleh mengesahkan bahawa jenama kelas yang tinggal adalah: 162, 167, 172 dan 177 cm.

Menentukan jenama kelas adalah penting, kerana mereka perlu mencari aritmetik min dan varians pengedaran.

Langkah -langkah kecenderungan pusat dan penyebaran untuk data dikumpulkan

Langkah -langkah kecenderungan pusat yang paling banyak digunakan adalah purata, median dan fesyen, dan menerangkan dengan tepat kecenderungan data yang akan dikumpulkan di sekitar nilai pusat tertentu.

Separuh

Ini adalah salah satu langkah kecenderungan utama utama. Dalam data yang dikumpulkan, min aritmetik boleh dikira menggunakan formula:

 Di mana:

-X adalah purata

-F_Yo adalah kekerapan kelas

-m_Yo Ia adalah jenama kelas

-G adalah bilangan kelas

-n ialah jumlah data

Median

Untuk median anda perlu mengenal pasti selang di mana pemerhatian n/2 terletak. Dalam contoh kami pemerhatian ini adalah nombor 50, kerana terdapat sejumlah 100 data. Pemerhatian ini berada dalam selang 165-169 cm.

Kemudian anda perlu interpolasi untuk mencari nilai berangka yang sepadan dengan pemerhatian itu, yang mana formula digunakan:

Di mana:

-C = lebar selang di mana median terletak

-B_M = Sempadan bawah selang yang dimiliki median

-F_m = Jumlah pemerhatian yang terkandung dalam selang median

-N/2 = separuh daripada jumlah data

-F_BM = Jumlah bilangan pemerhatian sebelum selang median

Fesyen

Untuk fesyen, kelas modal dikenal pasti, yang mengandungi kebanyakan pemerhatian, yang jenama kelasnya dikenali.

Boleh melayani anda: piramid heksagon

Varians dan sisihan piawai

Varians dan sisihan piawai adalah langkah penyebaran. Sekiranya kita menunjukkan varians dengan s² Dan kepada sisihan piawai, iaitu akar kuadrat varians sebagai s, untuk data dikumpulkan yang kita akan mempunyai:

Dan

Latihan diselesaikan

Untuk pengagihan kedudukan pelajar universiti yang dicadangkan pada mulanya, hitung nilai -nilai:

a) purata

b) sederhana

c) Fesyen

d) varians dan sisihan piawai.

Rajah 2. Ketika datang ke banyak nilai, seperti statur kumpulan besar pelajar, lebih baik untuk mengumpulkan data dalam kelas. Sumber: Pixabay.

Penyelesaian kepada

Mari bina jadual berikut untuk memudahkan pengiraan:

Melalui ungkapan untuk kumpulan purata yang dikumpulkan di atas:

Menggantikan nilai dan melaksanakan jumlahnya secara langsung:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Penyelesaian b

Selang yang dimiliki median adalah 165-169 cm kerana selang waktu paling kerap.

Mari kita kenal pasti setiap nilai ini dalam contoh, dengan bantuan Jadual 2:

C = 5 cm (lihat bahagian amplitud)

B_M = 164.5 cm

F_m = 47

N/2 = 100/2 = 50

F_BM = 20

Menggantikan dalam formula:

Penyelesaian c

Selang yang terkandung dalam kebanyakan pemerhatian ialah 165-169 cm, jenamanya kelasnya adalah 167 cm.

Penyelesaian d

Kami mengembangkan jadual sebelumnya dengan menambahkan dua lajur tambahan:

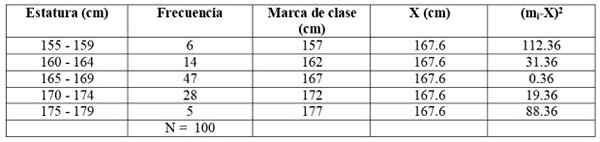
Kami menggunakan formula:

Dan kita mengembangkan jumlahnya:

s² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Oleh itu:

S = √21.35 cm² = 4.6 cm

Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. Canavos, g. 1988. Kebarangkalian dan Statistik: Aplikasi dan Kaedah. McGraw Hill.
3. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
4. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
5. Spiegel, m. 2009. Statistik. Siri Schaum. 4 ta. Edisi. McGraw Hill.
6. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.