Peringkat Kitaran Carnot, Aplikasi, Contoh, Latihan

Dia Kitaran Carnot Ia adalah urutan proses termodinamik yang berlaku dalam enjin Carnot, peranti ideal yang hanya terdiri daripada proses yang boleh diterbalikkan; iaitu, mereka yang, yang telah berlaku, boleh kembali ke keadaan awal.

Enjin jenis ini dianggap ideal, kerana ia tidak mempunyai pelesapan, geseran atau kelikatan yang timbul dalam mesin sebenar, menjadikan tenaga terma menjadi kerja yang boleh digunakan, walaupun penukaran tidak dilakukan 100%.

Rajah 1. Lokomotif stim. Sumber: Pixabay

Enjin dibina berdasarkan bahan yang mampu melakukan kerja, seperti gas, petrol atau stim. Bahan ini tertakluk kepada pelbagai perubahan suhu dan seterusnya mengalami variasi dalam tekanan dan kelantangannya. Dengan cara ini adalah mungkin untuk menggerakkan omboh di dalam silinder.

[TOC]

Apakah kitaran Carnot?

Kitaran Carnot berlaku dalam sistem yang dipanggil Carnot atau C Motor, yang merupakan gas yang ideal terkunci dalam silinder dan disediakan dengan omboh, yang bersentuhan dengan dua sumber pada suhu yang berbeza t₁ dan t₂ seperti yang ditunjukkan dalam angka berikut di sebelah kiri.

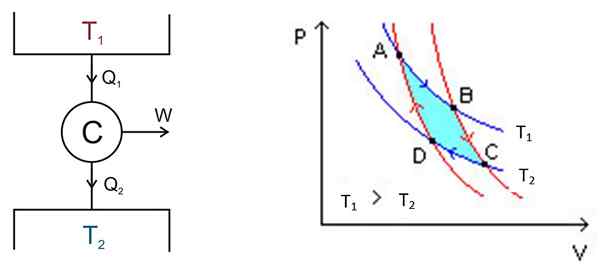Rajah 2. Di sebelah kiri skema mesin c arnot, di sebelah kanan gambarajah PV. Sumber Rajah Kiri: Keta - Kerja Sendiri, CC oleh 2.5, https: // commons.Wikimedia.org/w/indeks.Php?Curid = 681753, angka kanan Wikimedia Commons.

Terdapat proses berikut dalam mod kasar:

1. Sejumlah haba dibekalkan ke peranti_{pintu masuk} = Q₁ Dari tangki terma pada suhu tinggi t₁.
2. Enjin Carnot C melakukan kerja dengan terima kasih kepada haba ini yang dibekalkan.
3. Sebahagian daripada haba yang digunakan: sisa q_keluar, Ia dipindahkan ke tangki terma yang berada pada suhu yang lebih rendah t₂.

Tahap kitaran Carnot

Analisis dibuat oleh rajah p -v (tekanan -volume), seperti yang ditunjukkan dalam Rajah 2 (angka kanan). Matlamat motor adalah untuk menyimpan deposit termal 2 sejuk, mengekstrak haba daripadanya. Dalam kes ini ia adalah Mesin penyejuk. Jika sebaliknya anda ingin memberikan haba ke deposit terma 1 maka itu adalah Pam haba.

Rajah p -v menunjukkan perubahan tekanan - suhu enjin di bawah dua keadaan:

- Mengekalkan suhu malar (proses isoterma).

- Tiada pemindahan haba (penebat haba).

Kedua -dua proses isoterma perlu disambungkan, yang dicapai dengan cara penebat haba.

Titik

Anda boleh bermula pada bila -bila masa dalam kitaran, di mana gas mempunyai tekanan, jumlah dan suhu tertentu. Gas mengalami beberapa proses dan boleh kembali ke keadaan permulaan untuk memulakan kitaran lain, dan selalu tenaga dalaman akhir adalah sama dengan awal. Oleh kerana tenaga dipelihara:

Kerja yang dilakukan oleh C = haba input - haba berlepas

ΔW = q_{pintu masuk} - Q_keluar

Kawasan yang termasuk dalam kitaran atau gelung ini, dalam turquoise dalam angka, sama dengan kerja yang dilakukan oleh enjin Carnot.

Mata A, B, C dan D ditandakan dalam Rajah 2. Ia akan bermula pada titik untuk mengikuti anak panah biru.

Peringkat Pertama: Pengembangan Isoterma

Suhu antara titik a dan b ialah t₁. Sistem menyerap haba dari deposit haba 1 dan mengalami pengembangan isoterma. Kemudian jumlahnya meningkat dan tekanan berkurangan.

Walau bagaimanapun, suhu kekal dalam t₁, Sejak ketika gas mengembang ia menyejukkan. Oleh itu, tenaga dalamannya tetap berterusan.

Ia boleh melayani anda: Graff Van Generator: Pihak, Bagaimana Ia Berfungsi, Aplikasi

Tahap Kedua: Pengembangan Adiabatik

Pada titik b sistem memulakan pengembangan baru di mana sistem tidak menang atau kehilangan haba. Ini dicapai dengan meletakkannya dalam penebat kalori seperti yang ditunjukkan sebelumnya. Oleh itu, ia adalah pengembangan adiabatik yang terus menunjuk C berikutan anak panah merah. Jumlahnya meningkat dan tekanan berkurangan sehingga mencapai nilai terendahnya.

Tahap Ketiga: Mampatan Isothermal

Mulakan pada titik c dan berakhir di D. Penebat dikeluarkan dan sistem bersentuhan dengan deposit terma 2, yang suhunya t₂ Ia kurang. Sistem menghasilkan haba sisa ke tangki terma, tekanan mula meningkat dan jumlahnya berkurangan.

Peringkat Keempat: Mampatan Adiabatik

Sampai ke titik d, sistem kembali ke penebat haba, tekanan meningkat dan jumlahnya berkurangan sehingga mencapai keadaan asal titik a. Kemudian kitaran diulang lagi.

Teorem Carnot

Teorem Carnot pertama kali dirumuskan pada awal abad ke -19 oleh ahli fizik Perancis Sadi Carnot. Pada tahun 1824 Carnot, yang merupakan sebahagian daripada Tentera Perancis, menerbitkan sebuah buku di mana beliau mencadangkan jawapan kepada soalan berikut: Di bawah keadaan apa mesin terma mempunyai kecekapan maksimum? Carnot kemudian menubuhkan perkara berikut:

Tiada enjin haba yang berjalan di antara dua deposit haba lebih cekap daripada enjin Carnot.

Hasil η enjin haba diberikan oleh nisbah antara kerja yang dilakukan w dan haba yang diserap Q:

prestasi = kerja selesai/haba diserap

Dengan cara ini, prestasi mana -mana enjin terma i ialah: η = w/q. Walaupun prestasi enjin Carnot R adalah η '= w/q', dalam hal kedua -dua enjin mereka dapat melaksanakan pekerjaan yang sama.

Teorem Carnot menyatakan bahawa η tidak pernah lebih besar daripada η '. Jika tidak, ia akan bertentangan dengan undang -undang termodinamik kedua, mengikut mana proses di mana hasilnya adalah haba dari badan suhu yang lebih rendah adalah mustahil untuk pergi ke satu lagi suhu yang lebih tinggi tanpa menerima bantuan luaran. Oleh itu:

η _< η^'

Demonstrasi Teorem Carnot

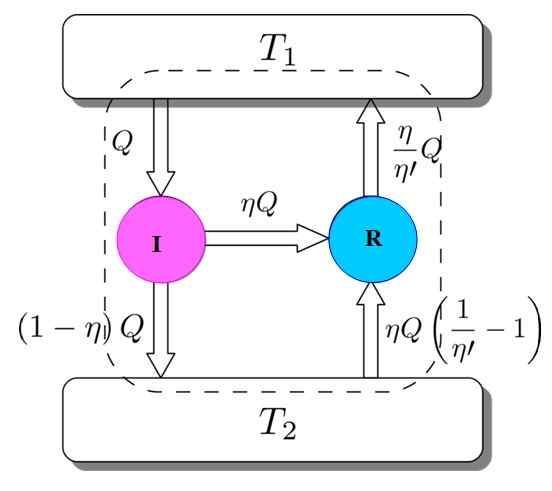
Untuk menunjukkan bahawa ini begitu, pertimbangkan enjin Carnot bertindak sebagai mesin peti sejuk yang didorong oleh enjin i. Ini mungkin kerana enjin Carnot berfungsi dengan proses yang boleh diterbalikkan, seperti yang dinyatakan pada mulanya.

Rajah 3. Demonstrasi Teorem Carnot. Sumber: Netheril96 [CC BY-SA 3.0 (https: // creativeCommons.Org/lesen/by-sa/3.0)]

Anda mempunyai kedua -duanya: i dan r bekerja dengan deposit terma yang sama dan ia akan diandaikan bahawa η _> η^'. Sekiranya di sepanjang jalan percanggahan dicapai dengan undang -undang termodinamik kedua, teorem Carnot ditunjukkan oleh pengurangan kepada kemustahilan.

Rajah 3 membantu mengikuti proses. Enjin I mengambil sejumlah haba q, yang membahagikan dengan cara ini: melakukan kerja pada r bersamaan dengan w = ηq dan selebihnya adalah haba yang dipindahkan (1 - -) q ke tangki termal t₂.

Oleh kerana tenaga dipelihara, semuanya dipenuhi:

Dan_{pintu masuk} = Q = kerja w + haba yang diberikan kepada t₂ = ηq + (1 - -) q = e_keluar

Sekarang mesin peti sejuk Carnot R mengambil tangki termal 2 jumlah haba yang diberikan oleh:

Ia boleh melayani anda: Imantation: Apa yang terdiri, kaedah dan contoh

(η / η ') (1 - -') q =

Tenaga juga mesti disimpan dalam kes ini:

Dan_{pintu masuk} = ηq + (η / η ') (1 - -') q = (η / η ') q = q' = e_keluar

Hasilnya ialah pemindahan ke tangki termal t₂ daripada jumlah haba yang diberikan oleh (η / η ') q = q'.

Sekiranya η lebih besar daripada η 'ini bermakna deposit terma suhu tertinggi telah tiba lebih panas daripada yang saya ambil pada asalnya. Oleh kerana tidak ada ejen luaran, seperti sumber terma yang lain, telah mengambil bahagian, satu -satunya cara yang boleh berlaku ialah deposit terma yang paling sejuk menghasilkan haba.

Ini tidak bersetuju dengan undang -undang termodinamik kedua. Disimpulkan maka tidak mungkin η^' Kurang daripada η, oleh itu enjin I tidak boleh mempunyai lebih banyak prestasi daripada mesin Carnot R.

Teorem corollary dan batasan

The Carnot Theorem Corollary menyatakan bahawa dua mesin Carnot mempunyai kecekapan yang sama jika kedua -duanya beroperasi dengan deposit terma yang sama.

Ini bermakna bahawa bahan itu tidak penting, prestasi itu bebas dan tidak dapat dibangkitkan dengan mengubahnya.

Kesimpulan analisis sebelumnya adalah bahawa kitaran Carnot adalah bahagian atas proses termodinamik yang dapat dicapai. Dalam amalan terdapat banyak faktor yang mengurangkan kecekapan, contohnya fakta bahawa pengasingan tidak pernah sempurna dan di peringkat adiabatik sebenarnya ada pertukaran kalori dengan luaran.

Sekiranya berlaku kereta, blok enjin dipanaskan. Sebaliknya, campuran gas dan udara tidak berkelakuan tepat sebagai gas yang ideal, yang merupakan titik permulaan kitaran Carnot. Ini hanya menyebut beberapa faktor yang akan menyebabkan pengurangan prestasi drastik.

Contoh

Omboh di dalam silinder

Sekiranya sistem adalah omboh yang terkunci dalam silinder seperti dalam Rajah 4, omboh meningkat semasa pengembangan isoterma, seperti yang dapat dilihat dalam skema pertama yang tersisa dan juga meningkat semasa pengembangan adiabatik.

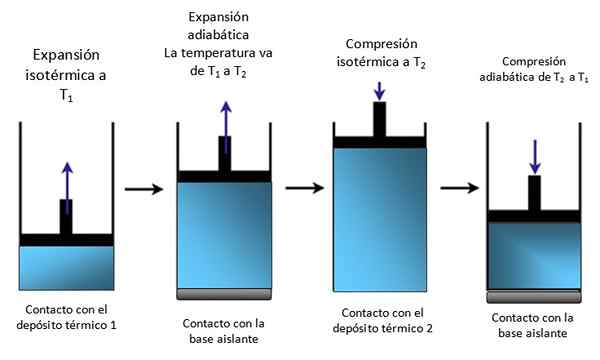Rajah 4. Pergerakan omboh di dalam silinder. Sumber: Diri Diri.

Kemudian dimampatkan secara isothermically, memberi haba, dan terus memampatkan secara adiabatically. Hasilnya adalah pergerakan di mana omboh naik dan turun di dalam silinder dan boleh dihantar ke bahagian lain dari peranti tertentu, seperti enjin kereta misalnya, yang menghasilkan pasangan, atau mesin beruap.

Pelbagai proses boleh diterbalikkan

Sebagai tambahan kepada pengembangan dan pemampatan gas yang ideal di dalam silinder, terdapat proses terbalik ideal yang lain yang boleh dikonfigurasikan, sebagai contoh:

- Pergerakan perjalanan bulat tanpa ketiadaan geseran.

- Musim bunga yang ideal yang dimampatkan dan dikompresi dan tidak pernah berubah bentuk.

- Litar elektrik di mana tidak ada rintangan yang menghilangkan tenaga.

- Kitaran magnetisasi dan demagnetisasi di mana tidak ada kerugian.

- Memuat dan memuat turun bateri.

Loji tenaga nuklear

Walaupun ia adalah sistem yang sangat kompleks, pendekatan pertama yang diperlukan untuk menghasilkan tenaga dalam reaktor nuklear adalah yang berikut:

- Sumber terma, yang terdiri daripada bahan yang hancur secara radioaktif seperti uranium.

Boleh melayani anda: Model atom semasa

- Deposit terma tenggelam atau sejuk yang akan menjadi atmosfera.

- "Mesin Carnot" yang menggunakan cecair, hampir selalu mengalir air, yang dibekalkan haba dari sumber terma untuk menjadikannya stim.

Apabila kitaran dijalankan, elektrik diperolehi sebagai kerja bersih. Apabila berubah menjadi stim suhu tinggi, air dicapai ke turbin, di mana tenaga berubah menjadi pergerakan atau tenaga kinetik.

Turbin seterusnya mengaktifkan penjana elektrik yang mengubah tenaga pergerakannya menjadi elektrik. Sebagai tambahan kepada bahan fistening seperti uranium, tentu saja bahan api fosil dapat digunakan sebagai sumber haba.

Latihan yang diselesaikan

-Contoh 1: Kecekapan mesin terma

Kecekapan mesin terma ditakrifkan sebagai nisbah antara kerja output dan kerja masuk, dan oleh itu adalah jumlah yang tidak dimensi:

Kecekapan maksimum = (q_{pintu masuk} - Q _keluar) /Q_{pintu masuk}

Menandakan kecekapan maksimum sebagai e_maks, Adalah mungkin untuk menunjukkan pergantungan suhunya, yang merupakan pemboleh ubah yang paling mudah untuk diukur, seperti:

dan_maks = 1 - (t₂/T₁)

Di mana t₂ Ia adalah suhu sinki dan t₁ Ia adalah suhu sumber terma. Oleh kerana yang terakhir lebih besar, kecekapan selalu menjadi kurang dari 1.

Katakan bahawa mesin terma mampu bekerja dengan cara berikut: a) antara 200 k dan 400 k, b) antara 600 k dan 400 k. Apakah kecekapan dalam setiap kes?

Penyelesaian

a) Dalam kes pertama kecekapan adalah:

dan_Max1 = 1 - (200/400) = 0.lima puluh

b) Untuk mod kedua kecekapan akan:

dan_Max2 = 1- (400/600) = 0.33

Walaupun perbezaan suhu adalah sama antara kedua -dua mod, kecekapan tidak. Dan lebih ketara ialah mod yang paling berkesan beroperasi pada suhu yang lebih rendah.

-Contoh 2: Haba yang diserap dan panas

Mesin terma sebanyak 22 % menghasilkan 1530 j kerja. Cari: a) Jumlah haba yang diserap dari deposit haba 1, b) jumlah haba yang dibuang ke tangki termal 2.

a) Dalam kes ini definisi kecekapan digunakan, kerana kerja yang dilakukan, bukan suhu deposit terma tersedia. Kecekapan 22% bermaksud bahawa e _Maks = 0.22, oleh itu:

Kecekapan maksimum = kerja /q_{pintu masuk}

Jumlah haba yang diserap adalah tepat Q_{pintu masuk}, Jadi penjelasan yang anda ada:

Q_{pintu masuk} = Kerja/kecekapan = 1530 J/0.22 = 6954.5 J

b) Jumlah haba yang diberikan kepada tangki paling sejuk adalah dari δW = Q_{pintu masuk} - Q_keluar

Q_keluar = Q_{pintu masuk} - ΔW = 6954.5 -1530 J = 5424.5 J.

Cara lain adalah dari dan_maks = 1 - (t₂/T₁). Oleh kerana suhu tidak diketahui, tetapi ini berkaitan dengan haba, kecekapan juga boleh dinyatakan sebagai:

dan_maks = 1 - (Q_Sceding/Q_diserap)

Rujukan

1. Bauer, w. 2011. Fizik untuk Kejuruteraan dan Sains. Jilid 1. MC Graw Hill. 654-657
2. Tenaga nuklear. Operasi loji tenaga nuklear. Pulih dari: tenaga nuklear.jaring
3. Serway, r., Jewett, J. (2008). Fizik untuk Sains dan Kejuruteraan. Jilid 1. Ke -7. Ed. Pembelajaran Cengage. 618-622.
4. Tippens, ms. 2011. Fizik: Konsep dan aplikasi. Edisi ke -7. Macgraw Hill. 414-416.
5. Walker, J.2008. Fizik. Edisi ke -4.Addison Wesley. 610-630