Bagaimana mendapatkan peratusan? Contoh dan latihan

Boleh Dapatkan peratusan Dengan beberapa kaedah. Anda boleh dengan cepat mengira 10% daripada mana -mana nombor hanya apabila menggerakkan kedudukan perpuluhan anda ke kiri. Sebagai contoh, 10% daripada 100 adalah 10; 10% daripada 1000 adalah 100.

Sekiranya anda ingin mengira peratusan yang lebih kompleks seperti 36% daripada 25 atau 250% daripada 20, kaedah lain diperlukan. Bagi kes di mana sistem 10% tidak berkenaan, metodologi berikut boleh diambil kira.

Rajah 1. Diskaun dengan peratusan yang berbeza. Berapa banyak kita saling menyelamatkan?. Sumber: Pixabay.

Peratusan istilah bermaksud bahagian tertentu setiap ratus dan merujuk kepada operasi aritmetik yang dijalankan untuk mencari bahagian tersebut. Contohnya 20% ("Dua Puluh Peratus") dibaca di Pesos, ini bermakna 20 peso didiskaunkan untuk setiap 100 peso.

Peratusan berkhidmat untuk mengira bahagian mana dari jumlah mewakili jumlah. Dalam kes ini, jumlahnya diambil ke skala 100 dan peratusan memberitahu berapa banyak, berdasarkan 100, adalah bahagian yang akan dikira.

Mari lihat bagaimana ia dilakukan dengan contoh -contoh ini. Di tempat pertama kita melakukannya dalam bentuk pecahan:

• 20% = 20/100
• 5% = 5/100
• 0.7% = 0.7 / 100
• 100% = 100/100

Perhatikan bahawa 100% adalah sama dengan 1. Tetapi peratusan juga boleh ditulis perpuluhan:

• 20% = 0.20
• 5% = 0.05
• 0.7% = 0.007
• 100% = 1.0

Apabila peratusan bilangan tertentu dinyatakan, hanya Koma bergerak Dari nombor dua tempat di sebelah kiri. Dalam peratusan, peraturan proporsional:

20% adalah 20 daripada 100, oleh itu:

20% daripada 100 adalah 20, 20% daripada 200 adalah 40, 20% daripada 300 adalah 60, 20% daripada 50 adalah 10.

Peraturan Am untuk 20 % daripada apa -apa jumlah

20% daripada x adalah x *(20/100) = x *0.2 = 0.2 *x

Peraturan ini dapat dengan mudah diperluaskan untuk mencari peratusan lain yang dikehendaki. Mari lihat bagaimana di bahagian berikut.

Latihan diselesaikan dengan formula untuk mengira n% 

Formula untuk meringkaskan secepat mungkin dan cepat mengira sebarang peratusan n adalah:

n % =(A * n)/100

Contohnya anda ingin mengira 25% daripada 400

Kemudian n = 25 dan A = 400, menghasilkan (400*25)/100 = 100

Contoh

Berapakah peratusan 60 adalah 24?

Penyelesaian

Apa yang diminta bersamaan dengan bertanya apakah n% daripada 60 yang memberikan 24?

Kami mencadangkan formula umum:

60 * n / 100 = 24

Kita jelas n Dengan prosedur ini:

-100 yang membahagikan ahli iZiédo Persamaan, pergi ke ahli betul mendarab. 

-Dan 60 yang berlipat ganda dalam ahli dibiarkan Pergi ke ahli betul membahagikan.

N = 24 *100/60 = 2400/60 = 240/6 = 6 *40/6 = 40

Disimpulkan bahawa 40% daripada 60 adalah 24.

Latihan pengiraan peratusan yang diselesaikan 

Di bawah adalah latihan mudah untuk mula mengamalkan yang disebutkan di atas.

Ia dapat melayani anda: 15 legenda dan mitos yang paling popular

Latihan 1

Cari 50% daripada 90.

Penyelesaian

Di sini x = 90, n = 50 % dan ganti:

90 * 50% = 90 * (50/100) = 4500 /100 = 45 

Ini agak mudah, kerana 50 % daripada jumlah apa -apa adalah separuh daripada jumlah itu dan separuh daripada 90 adalah 45.

Latihan 2

Cari 30% daripada 90.

Penyelesaian

90 * 30% = 90 * (30/100) = 2700 /100 = 27

Peratusan meningkat

Ia kerap dalam kehidupan seharian untuk mendengar peningkatan sesuatu, contohnya peningkatan pengeluaran, kenaikan gaji atau kebangkitan produk. Hampir selalu dinyatakan dalam bentuk peratusan.

Sebagai contoh, produk tertentu berharga € 300 tetapi mengalami peningkatan sebanyak 30%. Kami bertanya kepada diri sendiri: berapakah harga produk baru?

Yang pertama adalah untuk mengira bahagian yang sepadan dengan peningkatan. Oleh kerana peningkatan adalah 30 bahagian 100, jadi kenaikan kenaikan, berdasarkan harga asal 300, adalah tiga kali 30 bahagian, iaitu 3*30 = 90.

Produk ini meningkat € 90, jadi harga akhir baru akan menjadi kenaikan harga sebelum ini:

Harga Baru = Harga Lama + € 90 = € 390

Kita boleh membina formula untuk pengiraan kenaikan peratusan. Kami menggunakan huruf untuk melambangkan harga, seperti ini:

-F adalah nilai akhir

-Yo adalah nilai awal dan

-n Adakah kenaikan kenaikan.

Dengan nama -nama ini, nilai akhir akan dikira seperti ini:

f = i + (i* n / 100)

Tetapi bagaimana Yo Ia diulang dalam kedua -dua istilah, ia boleh diambil sebagai faktor biasaUntuk mendapatkan ungkapan lain ini, sama sah:

F = i * (1 + n / 100)

Mari sahkan dengan kes yang sudah diselesaikan, produk yang berharga € 300 dan meningkat 30%. Oleh itu, kami memastikan bahawa formula berfungsi dengan baik:

Harga Akhir = F = € 300 * (1 + 30/100) = € 300 * (1 + 0.3) = € 300 * 1.3 = € 390

Latihan 3

Seorang pekerja memperoleh € 1500, tetapi dinaikkan pangkat dan gajinya meningkat 20%. Berapakah gaji baru anda?

Penyelesaian

Mari gunakan formula:

F = € 1500 * (1 + 20/100) = € 1500 * (1 + 0.2) = € 1500 * 1.2 = € 1800

Gaji pekerja baru ialah € 1800.

Peratusan berkurangan

Dalam kes penurunan, formula untuk pengiraan nilai akhir F dari jumlah awal tertentu Yo yang mengalami penurunan dalam n% adalah:

F = i * (1 - n / 100)

Harus diingat bahawa tanda positif (+) formula di bahagian sebelumnya digantikan dengan tanda negatif (-).

Rajah 2. Notis Diskaun Peratusan. Sumber: Pixabay

Latihan 4

Produk yang ditandakan € 800, tetapi menerima diskaun 15%. Berapakah harga produk baru?

Penyelesaian 4

Harga akhir mengikut formula adalah:

F = € 800 * (1 - 15/100) = € 800 * (1 - 0.15) = € 800 * (0.85) = € 680

Harga akhir dengan diskaun 15% ialah € 680, yang mewakili penjimatan sebanyak € 120.

Peratusan berturut -turut

Nampaknya apabila jumlahnya mengalami variasi peratusan dan kemudian satu lagi digunakan, juga peratusan. Contohnya produk yang mempunyai dua diskaun peratusan berturut -turut. Contoh lain ialah pekerja yang mempunyai dua kenaikan gaji berturut -turut.

Boleh melayani anda: aktiviti ekonomi Yucatan yang lebih penting

- Peratusan berturut -turut meningkat

Pangkalan penyelesaian kes -kes ini adalah sama dengan kenaikan unik, tetapi perlu diambil kira bahawa kenaikan peratusan kedua dilakukan pada nilai akhir kenaikan pertama.

Katakan produk yang meningkat 10% pertama dan kemudian 5%. Tidak betul untuk mengatakan bahawa ia mengalami peningkatan sebanyak 15%, sebenarnya lebih daripada peratusan ini.

Formula untuk nilai akhir akan dikenakan seperti ini:

-Mula -mula nilai akhir kenaikan pertama n1% dikira

f1 = i + i * n1 / 100

-Dan kemudian, untuk mencari nilai akhir kenaikan kedua n2%, nilai akhir F1 diambil sebagai nilai awal. Oleh itu:

F2 = F1 + F1 * N2 /100 

Latihan 5

Sebuah buku yang mula -mula berharga € 55, tetapi disebabkan oleh kejayaan dan permintaannya yang tinggi, ia mengalami dua kenaikan berturut -turut pada harga asal. Peningkatan pertama adalah 10% dan yang kedua daripada 20%. Berapakah harga akhir buku?

Penyelesaian

-Peningkatan pertama:

F1 = € 55 * (1 + 10/100) = € 55 * 1.1 = € 60.5

-Peningkatan kedua

F2 = € 60.5 * (1 + 20/100) = € 60.5 * 1.2 = € 72.6

Harga akhir ialah € 72.6.

Latihan 6

Merujuk kepada latihan sebelumnya. Kedua -dua kenaikan berturut -turut: berapa peratusan kenaikan unik ke atas harga buku asal yang sesuai?

Penyelesaian

Jika kita memanggil N% kepada peratusan kenaikan unik, formula yang mengaitkan kenaikan peratusan unik ini kepada nilai asal dan nilai akhir adalah:

F2 = i *(1 + n / 100) 

Iaitu:

€ 72.6 = € 55 + 55 € * (n / 100)

Mengosongkan peningkatan peningkatan n% = (n /100), kita ada:

(N / 100) = (€ 72.6 - € 55) / 55 € = 17.€ 6 / € 55 = 0.32

Oleh itu:

N = 0.32 * 100 = 32

Pada harga buku, jumlah jumlah kenaikan sebanyak 32% telah digunakan. Perhatikan bahawa kenaikan ini lebih besar daripada jumlah dua peratusan berturut -turut meningkat.

- Diskaun peratusan berturut -turut

Idea ini serupa dengan peningkatan peratusan berturut -turut. Diskaun peratusan kedua mesti sentiasa digunakan untuk nilai akhir diskaun pertama, mari kita lihat contoh:

Latihan 7

Diskaun 10% diikuti dengan diskaun kedua sebanyak 20% pada objek, yang mana diskaun peratusan unik ia bersamaan?

Penyelesaian

-Diskaun pertama:

F1 = i - i * n1 / 100  

-Diskaun kedua

F2 = F1 - F1 * N2 / 100

Menggantikan persamaan pertama di tempat kedua:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Membangunkan ungkapan ini, kita dapat:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Menarik faktor umum Yo:

F2 = I * (1- N1% - N2% + N1% * N2%)

Akhirnya, peratusan yang ditunjukkan dalam soalan diganti:

F2 = I * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0.1 - 0.2 + 0.1 * 0.2)

f2 = i * (1 - 0.3 + 0.02) = i * (0.72) = i * (1 - 0.28) = i * (1 - 100/100) = i * (1 - 28%)

Dengan kata lain, diskaun berturut -turut sebanyak 10% dan 20% sesuai dengan diskaun 28% yang unik.

Latihan Lanjutan

Mari cuba latihan ini hanya apabila idea -idea yang sebelumnya sudah cukup jelas.

Ia boleh melayani anda: penutup geografi yang mudah dan indah, meliputi, gambar

Latihan 8

Pangkalan segitiga berukuran 10 cm dan ketinggian 6 cm. Sekiranya panjang asas berkurangan sebanyak 10%. Dalam peratusan berapa ketinggian akan ditingkatkan sehingga kawasan segitiga tidak berubah?

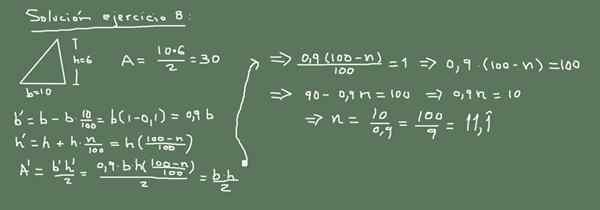Rajah 3. Penyelesaian Alternatif untuk Latihan 8. Disediakan oleh f. Zapata.

Penyelesaian 8

Kawasan segitiga asal adalah:

A = (10cm * 6cm) / 2 = 30 cm²

Sekarang, jika asas menurun sebanyak 10%, maka nilai baru adalah:

Asas baru = 10 - (10/100) x 10 = 9 cm.

Nilai ketinggian baru akan menjadi x, dan kawasan asal mesti tidak berubah, sehingga:

(9cm * x) /2 = 30 cm²

Kemudian nilai x dibersihkan sebagai:

X = 60 cm² / 9 cm = (20/3) cm = 6,666 cm

Yang bermaksud peningkatan sebanyak 0.666 berbanding dengan nilai asal. Mari kita lihat sekarang berapa peratusan ini mewakili:

6,666 = 6 + (6 * n/100) 

6,666 -6 = 6 * n/100

0.666 = 6 * n/100

N/100 = 0.111

N = 11.1

Jawapannya ialah: ketinggian mesti ditingkatkan sebanyak 11.1% untuk kawasan segitiga untuk kekal sama.

Latihan 9

Sekiranya gaji meningkat sebanyak 20%, tetapi kemudian diskaun cukai 5%, apakah kenaikan sebenar pekerja menerima?

Penyelesaian 

Mula -mula kita mengira peningkatan N1%:

f1 = i + i * n1 / 100

Kemudian kami menggunakan diskaun N2%:

F2 = F1 - F1 * N2 / 100

Persamaan pertama digantikan di tempat kedua:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Ungkapan sebelumnya berkembang:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Akhirnya ia dikeluarkan Yo Faktor umum dan nilai n1 = 20 dan n2 = 5 yang muncul dalam pernyataan diganti:

F2 = I (1 + 0.2 - 0.05 - 0.2* 0.05) = i* (1 + 7/50) = i* (1 + 14/100) = I* (1 + 14%)

Pekerja menerima kenaikan bersih sebanyak 14%.

Latihan 10

Tentukan apa yang paling mudah antara kedua -dua pilihan ini:

i) memperoleh t -shirt dengan diskaun 32 % masing -masing.

Ii) Beli 3 T -shirt untuk harga 2.

Penyelesaian 

Kami menganalisis setiap pilihan secara berasingan dan kemudian memilih yang paling menjimatkan:

i) Biarkan x menjadi harga semasa baju, diskaun 32 % mewakili harga akhir xf:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Contohnya, membeli 3 baju bermaksud membelanjakan 3 x 0.68 x = 2.04x

ii) Jika x adalah harga baju, untuk 3 baju anda hanya akan membayar 2x.

Katakan baju bernilai 6 euro, dengan diskaun 32 % akan bernilai 4.08 Euro. Beli 1 T -shirt bukan pilihan yang sah dalam tawaran 3 × 2. Oleh itu, jika anda hanya mahu membeli baju 1, diskaun lebih baik.

Tetapi jika apa yang anda mahukan adalah membeli untuk berpuluh -puluh, tawaran 3 × 2 hanya sedikit lebih murah. Contohnya, 6 T -shirt dengan diskaun akan keluar untuk 24.48 euro, manakala dengan tawaran 3 × 2 mereka akan menelan belanja 24 euro

Rujukan

1. Bilik darjah yang mudah. Peratusan. Diperolehi daripada: Bilik Darjah.com
2. Baldor a. 2006. Aritmetik teoritis praktikal. Edisi kebudayaan.
3. Anak -anak pendidikan. Cara belajar mengira peratusan. Pulih dari: pendidikan.com
4. Gutiérrez, g. Nota Matematik Kewangan. Pulih dari: csh.Izt.UAM.mx
5. Kutu pintar. Peratusan: apa dan bagaimana dikira. Pulih dari: Smartick.adalah