Formula Koefisien Penentuan, Pengiraan, Tafsiran, Contoh

Dia Pekali penentuan Ia adalah nombor antara 0 dan 1 yang mewakili pecahan mata (x, y) yang mengikuti garis pelarasan dengan regresi data yang ditetapkan dengan dua pembolehubah.

Ia juga dikenali sebagai kebaikan pelarasan dan dilambangkan oleh r². Untuk mengira ia, kuota diambil antara varians data ŷI yang dianggarkan oleh model regresi dan varians data YI yang sepadan dengan setiap xi data.

R² = Sŷ / sy

Rajah 1. Koefisien korelasi untuk empat pasangan data. Sumber: f. Zapata.

Sekiranya 100% data berada pada garis fungsi regresi, maka pekali penentuan akan menjadi 1.

Sebaliknya, jika untuk set data dan fungsi pelarasan tertentu, pekali r r r² Ternyata sama dengan 0.5, maka dapat dikatakan bahawa pelarasan itu memuaskan atau baik pada 50%. 

Begitu juga, apabila model regresi membuang nilai r r² kurang daripada 0.5, ini menunjukkan bahawa fungsi pelarasan yang dipilih tidak menyesuaikan dengan memuaskan data, oleh itu perlu untuk mencari fungsi pelarasan yang lain.

Dan bila kovarians atau Koefisien korelasi Ia cenderung kepada sifar, maka pembolehubah x dan y dari data tidak berkaitan, dan oleh itu r² juga akan cenderung sifar.

[TOC]

Cara mengira pekali penentuan?

Dalam bahagian sebelumnya, dikatakan bahawa pekali penentuan dikira dengan mencari kota antara variasi:

-Dianggarkan oleh fungsi regresi pembolehubah dan 

-Pembolehubah Yi sepadan dengan setiap pemboleh ubah xi. 

Dalam bentuk matematik, ia tetap seperti ini:

R² = Sŷ / sy

Dari formula ini ia mengikuti bahawa r² mewakili perkadaran varians yang dijelaskan oleh model regresi. Sebagai alternatif, R boleh dikira² Melalui formula berikut, sama dengan yang sebelumnya:

R² = 1 - (sε / sy)

Di mana sε mewakili varians sisa εi = ŷi - yi, manakala SY adalah varians set data data data. Untuk menentukan ŷI fungsi regresi digunakan, yang bermaksud mengesahkan bahawa ŷi = f (xi).

Ia boleh melayani anda: pecahan bersamaan dengan 3/5 (penyelesaian dan penjelasan)

Varians set data Yi, dengan i dari 1 hingga n dikira dengan cara ini:

Sy = [σ (yi -)² ) / (N-1)]

Dan kemudian meneruskan dengan cara yang sama untuk sŷ atau untuk sε.

Kes ilustrasi

Dengan cara menunjukkan perincian cara di mana pengiraan Pekali penentuan Kami akan mengambil set empat pasang data berikut: 

(X, y): (1, 1); (23); (3, 6) dan (4, 7).

Pelarasan regresi linear dicadangkan untuk set data ini yang diperolehi oleh kaedah minimum persegi:

f (x) = 2.1 x - 1 

Memohon fungsi pelarasan ini, rakan sebaya diperoleh:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) dan (4, 7.4).

Kemudian kami mengira aritmetik untuk x dan y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Varians sy

Sy = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +… .… .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Varians sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +… .… .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Koefisien penentuan r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Tafsiran

Koefisien penentuan untuk kes ilustrasi yang dipertimbangkan dalam segmen sebelumnya ternyata 0.98. Iaitu pelarasan linear melalui fungsi:

 f (x) = 2.1x - 1

98% boleh dipercayai untuk menerangkan data yang diperolehnya melalui kaedah minimum persegi. 

Sebagai tambahan kepada pekali penentuan, ada Koefisien korelasi linear atau juga dikenali sebagai pekali Pearson. Pekali ini, dilambangkan sebagai r, Ia dikira dengan hubungan berikut:

R = sxy / (sx sy)

Di sini pengangka mewakili kovarians antara pembolehubah x dan y, manakala penyebut adalah produk sisihan piawai untuk pembolehubah x dan sisihan piawai untuk pembolehubah dan.

Koefisien Pearson boleh mengambil nilai antara -1 dan +1. Apabila pekali ini cenderung kepada +1 terdapat korelasi linear langsung antara x dan y. Jika sebaliknya ia cenderung kepada -1, terdapat korelasi linear tetapi apabila x tumbuh dan berkurangan. Akhirnya, hampir 0 tidak ada kaitan antara kedua -dua pembolehubah.

Boleh melayani anda: Data berkumpul: Contoh dan senaman diselesaikan

Harus diingat bahawa pekali penentuan bertepatan dengan kuadrat pekali Pearson, hanya apabila yang pertama dikira berdasarkan pelarasan linear, tetapi kesamaan ini tidak sah untuk pelarasan bukan linear lain.

Contoh

- Contoh 1

Sekumpulan pelajar sekolah menengah berhasrat untuk menentukan undang -undang empirikal untuk tempoh pendulum sebagai fungsi panjangnya. Untuk mencapai matlamat ini, mereka membuat satu siri pengukuran di mana mereka mengukur masa ayunan pendulum untuk panjang yang berbeza mendapatkan nilai berikut:

Panjang (m)	Tempoh (s)
0.1	0.6
0.4	1.31
0.7	1.78
1	1.93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

Diminta untuk membuat graf penyebaran data dan membuat pelarasan linear dengan regresi. Di samping itu, tunjukkan persamaan regresi dan pekali penentuannya.

Penyelesaian

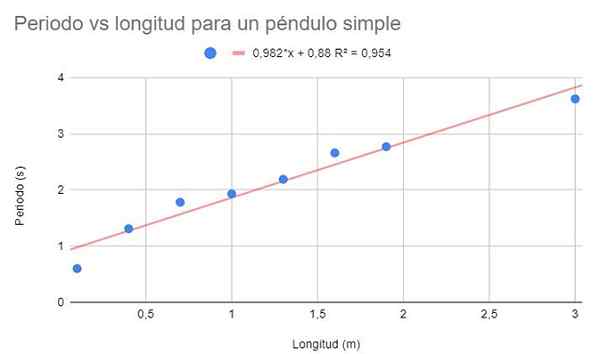Rajah 2. Penyelesaian Grafik Latihan 1. Sumber: f. Zapata.

Koefisien penentuan yang cukup tinggi (95%) dapat diperhatikan, jadi dapat dianggap bahawa pelarasan linear adalah optimum. Walau bagaimanapun, jika mata diperhatikan bersama, nampaknya mereka mempunyai kecenderungan untuk melengkung ke bawah. Perincian ini tidak dipertimbangkan dalam model linear.

- Contoh 2

Untuk data yang sama Contoh 1, buat carta penyebaran data. Pada kesempatan ini, tidak seperti Contoh 1, diminta untuk membuat pelarasan regresi melalui fungsi yang berpotensi.

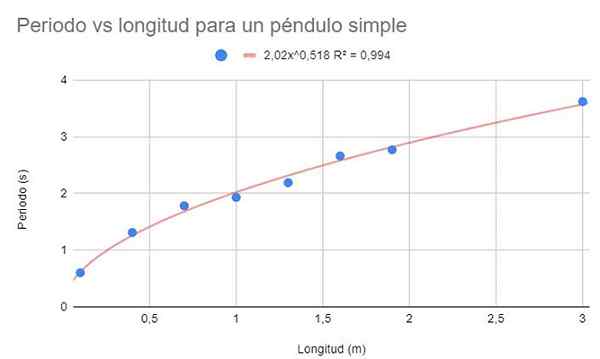Rajah 3. Penyelesaian Grafik Latihan 2. Sumber: f. Zapata.

Juga menunjukkan fungsi pelarasan dan pekali r -penentuannya².

Penyelesaian

Fungsi berpotensi adalah bentuk f (x) = kapak^B, di mana a dan b adalah malar yang ditentukan oleh kaedah minimum persegi.

Angka sebelumnya menunjukkan fungsi berpotensi dan parameternya, serta pekali penentuan dengan nilai yang sangat tinggi sebanyak 99%. Perhatikan bahawa data mengikuti kelengkungan garis trend.

Boleh melayani anda: prinsip aditif

- Contoh 3

Dengan data yang sama Contoh 1 dan Contoh 2, buat pelarasan polinomial kedua -dua. Tunjukkan graf, polinomial pelarasan dan pekali penentuan r r² wartawan.

Penyelesaian

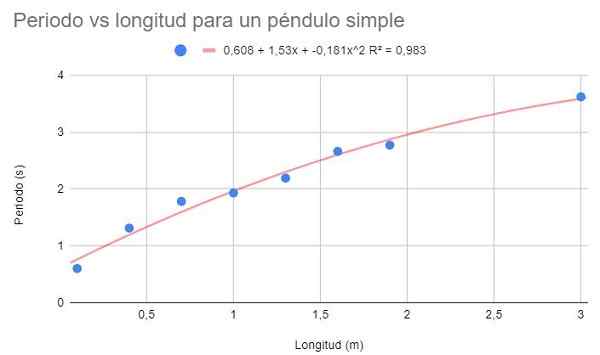Rajah 4. Grafik grafik 3 graf. Sumber: f. Zapata.

Dengan pelarasan polinomial darjah kedua, garis trend dapat dilihat dengan baik dengan kelengkungan data. Begitu juga, pekali penentuan melebihi pelarasan linear dan di bawah pelarasan potensial.

Perbandingan pelarasan

Daripada tiga pelarasan yang ditunjukkan, yang mempunyai pekali penentuan yang lebih tinggi adalah pelarasan yang berpotensi (Contoh 2).

Pelarasan yang berpotensi bertepatan dengan teori fizikal pendulum, yang, seperti yang diketahui, menetapkan bahawa tempoh pendulum adalah berkadar dengan akar kuadrat panjangnya, yang tetap berkadar 2π /√g di mana g adalah pecutan graviti.

Jenis pelarasan yang berpotensi ini bukan sahaja mempunyai pekali penentuan tertinggi, tetapi pemalar dan perkadaran yang berterusan bertepatan dengan model fizikal. 

Kesimpulan

-Pelarasan regresi menentukan parameter fungsi yang bertujuan untuk menerangkan data melalui kaedah minimum persegi. Kaedah ini terdiri daripada meminimumkan jumlah perbezaan kuadrat antara nilai dan pelarasan dan nilai yi data untuk nilai xi data. Dengan cara ini, parameter fungsi pelarasan ditentukan.

-Seperti yang telah kita lihat, fungsi pelarasan yang paling biasa adalah garis, tetapi bukan satu -satunya, kerana pelarasan juga boleh menjadi polinomik, potensi, eksponen, logaritma dan lain -lain. 

-Walau apa pun, pekali penentuan bergantung kepada data dan jenis pelarasan dan merupakan petunjuk kebaikan pelarasan yang digunakan.

-Akhirnya, pekali penentuan menunjukkan peratusan jumlah kebolehubahan antara nilai dan data berkenaan dengan nilai ŷ pelarasan untuk x yang diberikan.

Rujukan

1. González c. Statistik Umum. Pulih dari: tarwi.La Molina.Edu.PE
2. IACS. Institut Sains Kesihatan Aragonese. Diperolehi dari: ICS-Aragon.com
3. Salazar c. dan Castillo s. Prinsip Statistik Asas. (2018). Diperolehi dari: DSPACE.Uce.Edu.Ec
4. Superprof. Pekali penentuan. Pulih dari: superprof.adalah
5. USAC. Manual Statistik Deskriptif. (2011). Pulih dari: statistik.kejuruteraan.USAC.Edu.Gt.
6. Wikipedia. Pekali penentuan. Pulih dari: Adakah.Wikipedia.com.