Langkah -langkah kedudukan, kecenderungan pusat dan penyebaran

The Langkah -langkah kecenderungan pusat, penyebaran dan kedudukan, Ini adalah nilai yang digunakan untuk mentafsirkan satu set data statistik dengan betul. Ini boleh dilakukan secara langsung, seperti yang diperoleh dari kajian statistik, atau mereka boleh dianjurkan dalam kumpulan kekerapan yang sama, memudahkan analisis.

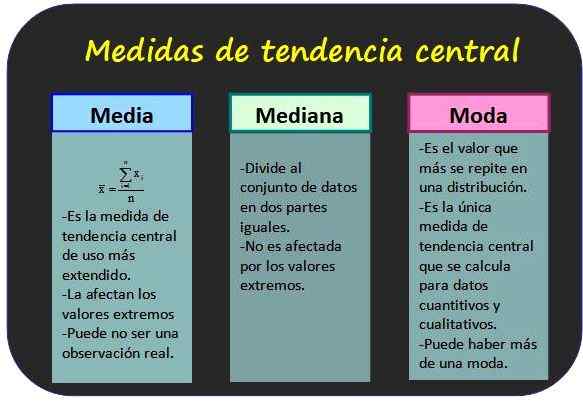
Tiga langkah trend pusat yang paling terkenal dan beberapa sifatnya. Sumber: f. Zapata.

Langkah kecenderungan pusat

Mereka membenarkan untuk mengetahui tentang nilai -nilai data statistik yang dikumpulkan bersama.

Purata aritmetik

Ia juga dikenali sebagai purata nilai pembolehubah dan diperoleh dengan menambahkan semua nilai dan membahagikan hasilnya dengan jumlah data.

• Aritmetik bermaksud data tanpa pengelompokan

Menjadi pemboleh ubah x yang tidak ada data tanpa menganjurkan atau mengumpulkan, min aritmetiknya dikira seperti berikut:

Dan dalam ringkasan notasi:

Contoh

Pemilik asrama pelancong gunung berhasrat untuk mengetahui berapa hari pelawat purata yang tinggal di kemudahan. Untuk melakukan ini, rekod hari -hari kekal 20 kumpulan pelancong telah dijalankan, mendapatkan data berikut:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Hari -hari purata yang tinggal di pelancong adalah:

= 2.5 hari

• Maksud aritmetik untuk data dikumpulkan

Jika data pembolehubah diatur dalam jadual kekerapan mutlak f f_Yo Dan pusat kelas adalah x₁, x₂,..., x_n, Purata dikira oleh:

Dalam penjumlahan musim panas:

Median

Median dari sekumpulan nilai n pembolehubah x adalah nilai pusat kumpulan, dengan syarat nilai -nilai semakin diperintahkan. Dengan cara ini, separuh daripada semua nilai lebih rendah daripada fesyen dan separuh lagi lebih besar.

• Sederhana data yang tidak berkumpul

Kes berikut boleh dibentangkan:

-Nilai N Nilai pembolehubah x  ganjil: Median adalah nilai yang hanya di tengah -tengah kumpulan nilai:

-Nilai N Nilai pembolehubah x pasangan: Dalam kes ini median dikira sebagai purata dua nilai pusat kumpulan data:

Contoh

Untuk mencari median data asrama pelancong, mereka mula -mula diperintahkan dari yang paling sedikit ke yang paling besar:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Ia dapat melayani anda: apakah kekerapan relatif dan bagaimana ia dikira?

Nombor data walaupun, oleh itu terdapat dua data pusat: x₁₀ dan x_sebelas Dan kerana kedua -duanya bernilai 2, purata juga.

Median = 2

• Sederhana data berkumpulan

Formula berikut digunakan:

Simbol -simbol dalam formula bermaksud:

-C: Lebar selang yang mengandungi median

-B_M: sempadan bawah selang yang sama

-F_m: bilangan pemerhatian yang mengandungi selang yang dimiliki oleh median.

-N: Jumlah data.

-F_BM: bilangan pemerhatian sebelum selang yang mengandungi median.

Fesyen

Fesyen untuk data yang tidak berkumpul adalah nilai kekerapan yang paling, sementara untuk data dikumpulkan, ia adalah kelas kekerapan yang paling banyak. Ia dianggap fesyen sebagai data yang paling mewakili atau kelas pengedaran.

Dua ciri penting dalam langkah ini ialah set data boleh mempunyai lebih daripada satu fesyen, dan fesyen dapat ditentukan untuk data kuantitatif dan data kualitatif.

Contoh

Meneruskan dengan data asrama pelancong, yang paling banyak diulangi adalah 1, oleh itu, perkara yang paling biasa adalah bahawa pelancong kekal 1 hari di asrama.

Langkah -langkah penyebaran

Langkah -langkah penyebaran menerangkan bagaimana mengumpulkan data di sekitar langkah -langkah pusat.

Julat

Ia dikira dengan menolak data utama dan data kecil. Sekiranya perbezaan ini besar, ia adalah tanda bahawa data disebarkan, sementara nilai -nilai kecil menunjukkan bahawa data itu hampir dengan purata.

Contoh

Julat untuk data asrama pelancong adalah:

Julat = 5-1 = 4

Varians

• Varians untuk data yang tidak berkumpul

Untuk mencari varians s² Perlu terlebih dahulu mengetahui purata aritmetik, maka perbezaannya dikira ke kuadrat antara setiap data dan purata, semuanya ditambah dan dibahagikan dengan jumlah pemerhatian. Perbezaan ini dikenali sebagai penyimpangan.

Varians, yang sentiasa positif (atau sifar), menunjukkan sejauh mana pemerhatian purata: jika varians tinggi, nilai -nilai lebih tersebar daripada ketika varians kecil.

Contoh

Varians untuk data asrama pelancong adalah:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Varians untuk data dikumpulkan

Untuk mencari varians sekumpulan data dikumpulkan, mereka diperlukan: i) purata, ii) kekerapan f_Yo  yang merupakan jumlah data dalam setiap kelas dan iii) x_Yo  atau nilai kelas:

Ia dapat melayani anda: jenis segitiga

Sisihan piawai

Penyimpangan piawai adalah akar kuadrat positif dari varians, jadi ia mempunyai kelebihan berbanding varians: ia datang dalam unit yang sama seperti pembolehubah yang sedang dikaji dan dengan itu mempunyai idea yang lebih langsung daripada yang dekat atau jauh yang pembolehubah rata -rata.

• Sisihan piawai untuk data yang tidak berkumpul

Ia ditentukan hanya dengan mencari akar kuadrat varians untuk data yang tidak disengajakan:

 Contoh

Penyimpangan piawai untuk data asrama pelancong adalah:

S = √ (s²) = √1.95 = 1.40

• Sisihan piawai untuk data dikumpulkan

Ia dikira dengan mencari akar kuadrat varians untuk data dikumpulkan:

Langkah -langkah kedudukan

Langkah -langkah kedudukan membahagikan set data yang teratur ke bahagian yang sama. Median, sebagai tambahan kepada ukuran kecenderungan utama juga merupakan ukuran kedudukan, kerana ia membahagikan keseluruhan menjadi dua bahagian yang sama. Tetapi anda boleh mendapatkan bahagian yang lebih kecil dengan kuartil, dekil dan persentil.

Kuartil

Kuartil membahagikan set ke empat bahagian yang sama, masing -masing dengan 25 % daripada data. Mereka dilambangkan sebagai q₁, Q₂ dan q₃ Dan median adalah kuartil q₂. Dengan cara ini, 25% daripada data berada di bawah kuartil Q₁, 50% di bawah kuartil Q₂ atau median dan 75% di bawah kuartil q₃.

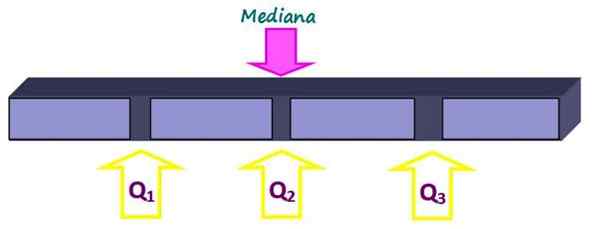Rajah 2. Kuartil membahagikan data yang ditetapkan menjadi empat bahagian yang sama. Sumber: f. Zapata.

• Kuartil untuk data yang tidak berkumpul

Data diperintahkan dan jumlahnya dibahagikan kepada 4 kumpulan dengan bilangan data yang sama masing -masing. Kedudukan kuartil pertama ditemui oleh:

Q₁ = (n+1)/4

Menjadi jumlah data. Sekiranya hasilnya adalah keseluruhan data yang sepadan dengan kedudukan itu, tetapi jika ia adalah perpuluhan, data yang sepadan dengan seluruh bahagian dengan yang berikut adalah purata, atau untuk ketepatan yang lebih besar ia diinterpolasi secara linear antara data tersebut.

Contoh

Kedudukan kuartil pertama q₁ Untuk data asrama pelancong adalah:

Q₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Ini adalah kedudukan kuartil 1 dan hasilnya adalah perpuluhan, data data x dicari₅ dan x_6, yang masing -masing x₅ = 1 dan x₆ = 1 dan mereka rata -rata, menghasilkan:

Kuartil pertama = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Kedudukan kuartil kedua q₂ adalah:

Boleh melayani anda: Jumlah teleskopik: Bagaimana ia diselesaikan dan diselesaikan latihan

Q₂ = 2 (n+1)/4 = 10.5

Yang rata -rata antara x₁₀ dan x_sebelas dan bertepatan dengan median:

Kuartil kedua = median = 2

Kedudukan kuartil ketiga dikira oleh:

Q₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Ia juga perpuluhan, oleh itu x adalah purata_{lima belas} dan x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Tetapi kerana kedua -duanya bernilai 4:

Kuartil ketiga = 4

Formula umum untuk kedudukan kuartil dalam data yang tidak disengajakan ialah:

Q_k = K (n+1)/4

Dengan k = 1,2,3.

• Kuartil untuk data dikumpulkan

Mereka dikira serupa dengan median:

Penjelasan simbol adalah:

-B_Q: Sempadan bawah selang yang mengandungi kuartil

-C: Lebar selang itu

-F_q: Bilangan pemerhatian yang mengandungi selang kuartil.

-N: Jumlah data.

-F_Bq: bilangan data sebelum selang yang mengandungi kuartil.

Deciles dan persentiles

Dekil dan persentil membahagikan data yang ditetapkan kepada 10 bahagian yang sama dan 100 bahagian yang sama masing -masing, dan pengiraan mereka dijalankan sama dengan kuartil.

• Dekil dan persentil untuk data yang tidak berkumpul

Formula digunakan masing -masing:

D_k = K (n+1)/10

Dengan k = 1,2,3 ... 9.

Decile d₅ Ia mesti sama dengan median.

P_k = K (n+1)/100

Dengan k = 1,2,3 ... 99.

Persentil p_{lima puluh} Ia mesti sama dengan median.

Contoh

Dalam contoh asrama pelancong, kedudukan d₃ adalah:

D₃ = 3 (20+1)/10 = 6.3

Bagaimana nombor perpuluhan purata x₆ dan x_7, kedua -duanya sama dengan 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Bermaksud bahawa 3 kesepuluh data di bawah x₇ = 1 dan baki di atas.

• Dekil dan persentil untuk data dikumpulkan

Formula sama dengan kuartil. D digunakan untuk menandakan dekil dan p untuk persentil dan simbol ditafsirkan dengan cara yang sama:

Peraturan empirikal

Apabila data diedarkan secara simetri dan pengedarannya tidak sama, ada peraturan yang dipanggil  Peraturan empirikal Sama ada Kaedah 68 - 95 - 99, yang kumpulan mereka dalam selang berikut:

• 68% daripada data berada dalam selang waktu:

• 95% daripada data berada dalam selang waktu:

• 99% daripada data berada dalam selang waktu:

Contoh

Dalam selang apa 95% data asrama pelancong?

Mereka berada dalam selang waktu: [2.5-1.40; 2.5+1.40] = [1.1; 3.9].

Rujukan

1. Berenson, m. 1985. Statistik untuk Pentadbiran dan Ekonomi. Inter -American s.Ke.
2. DEVORE, J. 2012. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk pentadbir. 2. Edisi. Prentice Hall.
4. Spiegel, m. 2009. Statistik. Siri Schaum. 4 ta. Edisi. McGraw Hill.
5. Walpole, r. 2007. Kebarangkalian dan statistik untuk kejuruteraan dan sains. Pearson.