Komponen segi empat tepat vektor (dengan latihan)

The Komponen segi empat tepat vektor adalah data yang membentuk vektor ini. Untuk menentukannya, perlu mempunyai sistem koordinat, yang biasanya pesawat Cartesian.

Sebaik sahaja anda mempunyai vektor dalam sistem koordinat, komponennya dapat dikira. Ini adalah 2, komponen mendatar (selari dengan paksi x), yang dipanggil "komponen dalam paksi x", dan komponen menegak (selari dengan paksi y), yang dipanggil "komponen dalam paksi y" ".

Perwakilan grafik komponen segi empat tepat vektor

Untuk menentukan komponen, perlu.

[TOC]

Cara menentukan komponen segi empat tepat vektor?

Untuk menentukan komponen ini, hubungan tertentu antara segi empat tepat dan fungsi trigonometri mesti diketahui.

Dalam gambar berikut, anda dapat melihat hubungan ini.

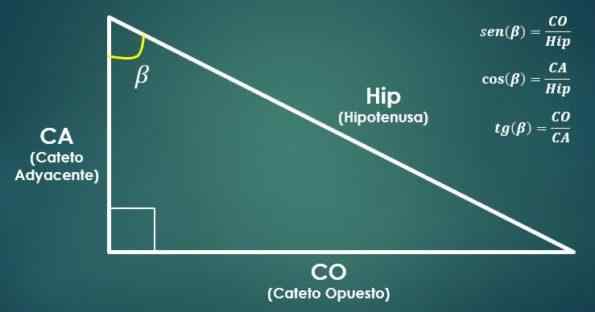Hubungan antara segi empat tepat dan fungsi trigonometri

Bosom sudut adalah sama dengan kuota antara ukuran cateto yang menentang sudut dan ukuran hipotenus.

Sebaliknya, kosinus sudut adalah sama dengan kuota antara ukuran cateto yang bersebelahan dengan sudut dan ukuran hipotenus.

Tangen sudut adalah sama dengan kuota antara ukuran kaki yang bertentangan dan ukuran cateto bersebelahan.

Dalam semua hubungan ini adalah perlu untuk menubuhkan segitiga segi empat tepat yang sepadan.

Adakah terdapat kaedah lain?

Yeah. Bergantung pada data yang disediakan, cara untuk mengira komponen segi empat tepat vektor boleh berbeza -beza. Alat lain yang banyak digunakan ialah Teorem Pythagoras.

Boleh melayani anda: Teorem kewujudan dan keunikan: demonstrasi, contoh dan latihan

Latihan yang diselesaikan

Latihan berikut dipraktikkan definisi komponen segi empat tepat vektor dan hubungan yang diterangkan di atas.

Latihan pertama

Diketahui bahawa vektor A mempunyai magnitud yang sama dengan 12 dan sudut yang bentuk ini dengan paksi x mempunyai ukuran 30 °. Tentukan komponen segi empat tepat vektor tersebut ke.

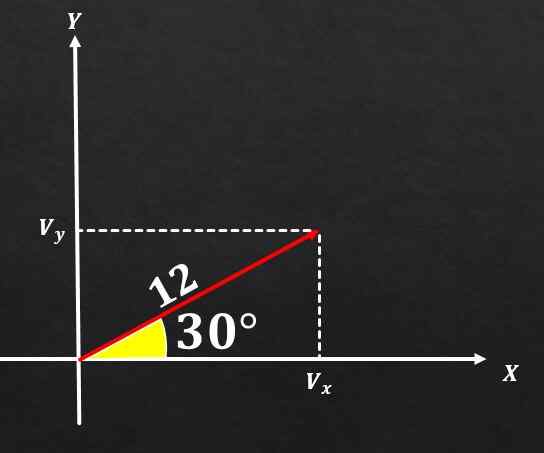
Penyelesaian

Sekiranya imej dihargai dan formula yang diterangkan di atas digunakan, dapat disimpulkan bahawa komponen dalam dan vektor A adalah sama dengan

dosa (30 °) = VY / 12, dan oleh itu VY = 12*(1/2) = 6.

Sebaliknya, komponen pada paksi x vektor A adalah sama dengan

cos (30 °) = vx / 12, dan oleh itu vx = 12*(√3 / 2) = 6√3.

Latihan kedua

Jika vektor A mempunyai magnitud sama dengan 5 dan komponen pada paksi x adalah sama dengan 4, tentukan nilai komponen A pada paksi y.

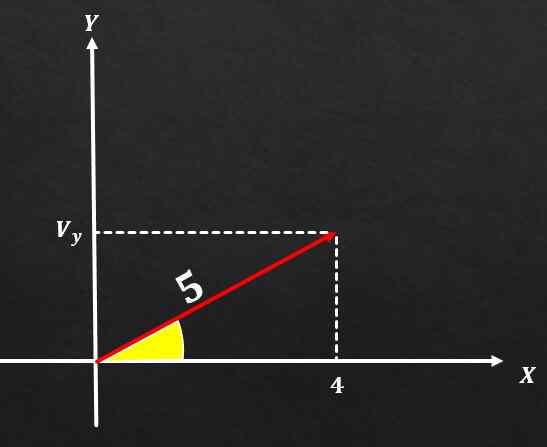
Penyelesaian

Menggunakan teorem pythagoras, magnitud vektor yang tinggi kuasa tinggi mestilah sama dengan jumlah kuadrat dua komponen segi empat tepat. Iaitu, m² = (vx) ² + (vy) ².

Menggantikan nilai yang disediakan, anda mesti

5² = (4) ² + (vy) ², oleh itu, 25 = 16 + (vy) ².

Ini menunjukkan bahawa (Vy) ² = 9 dan akibatnya Vy = 3.

Latihan ketiga

Jika vektor A mempunyai magnitud yang sama dengan 4 dan ini bentuk sudut 45 ° dengan paksi x, tentukan komponen segi empat tepat vektor tersebut.

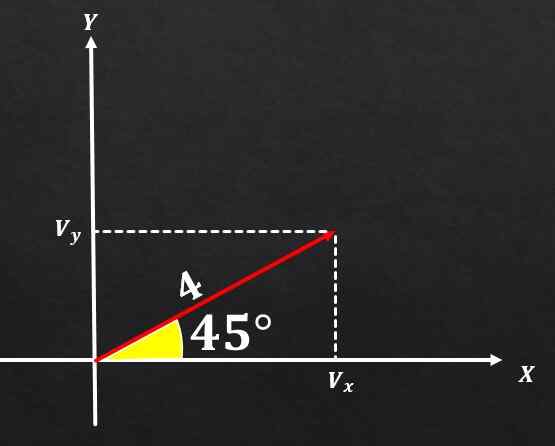
Penyelesaian

Menggunakan hubungan antara segitiga segi empat tepat dan fungsi trigonometri, dapat disimpulkan bahawa komponen pada dan vektor A adalah sama dengan

dosa (45 °) = Vy / 4, dan oleh itu Vy = 4*(√2 / 2) = 2√2.

Sebaliknya, komponen pada paksi x vektor A adalah sama dengan

Boleh melayani anda: penggantian kompaun

cos (45 °) = vx / 4, dan oleh itu vx = 4*(√2 / 2) = 2√2.

Rujukan

1. Landaverde, f. D. (1997). Geometri (Reprint ed.). Kemajuan.
2. Leake, d. (2006). Segitiga (Illustrated ed.). Heinemann-Raintree.
3. Pérez, c. D. (2006). Precalculation. Pendidikan Pearson.
4. Ruiz, á., & Barrantes, h. (2006). Geometri. Teknologi CR.
5. Sullivan, m. (1997). Precalculation. Pendidikan Pearson.
6. Sullivan, m. (1997). Trigonometri dan geometri analisis. Pendidikan Pearson.