Konsep mampatan dan formula, pengiraan, contoh, latihan

The usaha mampatan atau mampatan Ia adalah daya per unit kawasan yang hasilnya untuk menolak, mengetatkan atau memampatkan objek, cenderung untuk memendekkannya. Matematik adalah:

E = f /a

Di sini Dan Nyatakan usaha itu, F besar kekuatan dan Ke Kawasan di mana unit berada dalam sistem antarabangsa jika Newton/m² O Pascal (PA). Usaha mampatan adalah usaha biasa, kerana daya yang menghasilkannya berserenjang dengan kawasan yang mana ia dikenakan.

Rajah 1. Lajur di Acropolis of Athens tertakluk kepada pemampatan. Sumber: Pixabay.

Usaha sedemikian dapat memampatkan objek atau sebaliknya, mengetatkan dan meregangkannya, seperti yang digunakan. Dalam kes usaha mampatan, daya terpakai ke arah yang bertentangan untuk memberi kesan pengetatan dan memendekkan objek.

Sebaik sahaja pasukan berhenti, banyak bahan kembali ke dimensi asalnya. Harta ini dikenali dengan nama keanjalan. Tetapi ketika itu berlaku, ubah bentuk elastik kesatuan yang dialami oleh material yang tertakluk kepada usaha adalah:

UNISTARY Deformation = (Saiz Akhir - Saiz Awal)/Saiz Awal

Ubah bentuk boleh linear, dangkal atau kelantangan, walaupun ubah bentuk unit tidak mempunyai unit. Walau bagaimanapun, maklumat yang disediakannya sangat penting, kerana ia tidak sama untuk mengubah bentuk bar panjang 10 m dalam 1 cm, untuk mengubah bentuk 1cm bar panjang 1 m.

Dalam bahan elastik, ubah bentuk dan usaha berkadar, mematuhi undang -undang Hooke:

Usaha ∝ ubah bentuk kesatuan

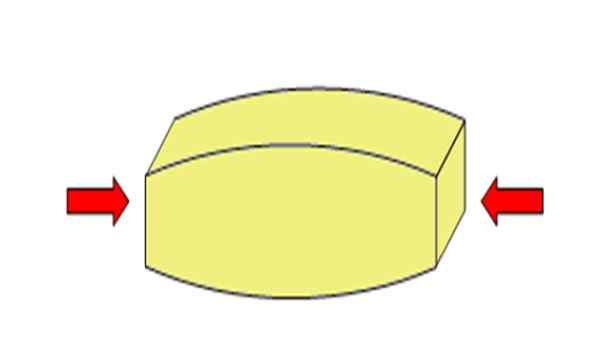Rajah 2. Usaha mampatan mengurangkan panjang objek. Sumber: Wikimedia Commons. Adre-es [cc by-sa 4.0 (https: // creativeCommons.Org/lesen/by-sa/4.0)].[TOC]

¿Cara mengira mampatan?

Usaha mampatan menjadikan zarah -zarah bahan semakin dekat dan lebih, memendekkan saiz mereka. Bergantung pada arah di mana usaha itu digunakan, akan ada pemendekan atau pengurangan dalam mana -mana dimensinya.

Boleh melayani anda: Model mekanikal kuantum atom

Mari kita mulakan dengan mengandaikan bar panjang yang nipis L,  ke mana usaha magnitud biasa digunakan Dan. Sekiranya usaha itu mampatan, bar mengalami pengurangan panjangnya, dilambangkan oleh δ. Sekiranya ketegangan, bar akan dilanjutkan.

Sememangnya, bahan yang dibuat oleh elemen adalah tegas dalam keupayaannya untuk menyokong usaha.

Ciri -ciri elastik bahan ini dimasukkan ke dalam pemalar perkadaran yang disebutkan di atas. Dipanggil Modul keanjalan Sama ada Modul muda dan ia dilambangkan sebagai dan. Setiap bahan mempunyai modul keanjalan, yang ditentukan secara eksperimen melalui ujian makmal.

Dengan ini, usaha Dan Ia dinyatakan dengan cara matematik seperti ini:

Usaha ∝ ubah bentuk kesatuan

Akhirnya, untuk menubuhkan keadaan ini sebagai persamaan, pemalar berkadar diperlukan untuk menggantikan simbol perkadaran ∝ dan menggantikannya dengan kesamaan, seperti ini:

Usaha = Perpadanan Pengubahsuaian X Unit tetap        

E = y. (Δ /l)

The Quotient (Δ /l) Ia adalah ubah bentuk kesatuan, dilambangkan sebagai ε dan dengan δ = Panjang Akhir - Panjang permulaan. Dengan cara ini, usaha Dan Ia tetap seperti:

E = y. ε

Oleh kerana ubah bentuk unit tidak berdimensi, unit Dan sama dengan yang Dan: N/m² atau PA di sistem SI, pound/in² o psi dalam sistem British, serta kombinasi kekuatan dan kawasan lain, seperti kg/cm².

Modul keanjalan bahan yang berbeza

Nilai dan ditentukan secara eksperimen di makmal, di bawah keadaan terkawal. Seterusnya, modul keanjalan untuk bahan yang digunakan secara meluas dalam pembinaan dan juga tulang:

Boleh melayani anda: vektor di ruang: Cara graf, aplikasi, latihan

Jadual 1

Bahan	Modul Keanjalan Y (PA) x 109
Keluli	200
Besi	100
Tembaga	100
Gangsa	90
Aluminium	70
Marmar	lima puluh
Granit	Empat lima
Konkrit	dua puluh
Tulang	lima belas
Pinewood	10

Contoh

Usaha mampatan bertindak pada pelbagai struktur; Sama seperti tindakan daya seperti berat setiap elemen yang mengarangnya, serta daya dari agen luaran: angin, salji, struktur lain dan banyak lagi.

Adalah biasa bagi kebanyakan struktur yang direka untuk menentang usaha semua jenis tanpa cacat. Oleh itu, perlu mengambil kira usaha mampatan untuk mengelakkan sekeping atau objek daripada kehilangan bentuknya.

Juga tulang kerangka adalah struktur tertakluk kepada pelbagai usaha. Walaupun tulang tahan terhadap mereka, apabila had elastik melebihi secara tidak sengaja, fissures dan fraktur berasal.

Lajur dan tiang

Lajur dan tiang bangunan mesti dibuat untuk menahan mampatan, jika tidak, mereka cenderung untuk mengatasi. Ini dikenali sebagai fleksi lateral Sama ada Buckling.

Lajur (lihat Rajah 1) adalah unsur -unsur yang panjangnya lebih tinggi berbanding dengan kawasan silangnya.

Unsur silinder adalah lajur apabila panjangnya sama dengan atau lebih besar daripada sepuluh kali diameter bahagian silang. Tetapi jika bahagian silang tidak tetap, diameternya yang lebih kecil akan diambil untuk tujuan mengklasifikasikan elemen sebagai lajur.

Kerusi dan bank

Apabila orang duduk di perabot seperti kerusi dan bank, atau tambahkan objek di atas, maka kaki tertakluk kepada usaha mampatan yang cenderung mengurangkan ketinggian mereka.

Rajah 3. Semasa duduk, orang membuat usaha mampatan di kerusi, yang cenderung memendekkan ketinggian mereka. Sumber: Pixabay.

Biasanya perabot dibuat untuk menahan berat badan dengan baik dan kembali ke keadaan semula jadi mereka setelah dikeluarkan. Tetapi jika berat badan yang besar diletakkan di kerusi atau bank yang rapuh, kaki menghasilkan mampatan dan pecah.

Boleh melayani anda: konduktor elektrik

Latihan

- Latihan 1

Anda mempunyai batang yang pada asalnya mengukur 12 m panjang, yang mana ia mengalami usaha mampatan sedemikian rupa sehingga ubah bentuk unitnya -0.0004. Berapakah panjang rod baru?

Penyelesaian

Bermula dari persamaan yang diberikan di atas:

ε = (Δ /l) = - 0.0004

Yeah L_F Ia adalah panjang terakhir dan L_{Sama ada} panjang awal, sejak δ = l_F - L_{Sama ada}  Kamu ada:

(L_F - L_{Sama ada})/ L_{Sama ada} = -0.0004

Oleh itu: L_F - L_{Sama ada} = -0.0004 x 12 m = -0.0048 m. Dan akhirnya:

L_F  = (12 - 0.0048) m = 11.9952 m.

- Latihan 2

Bar keluli pepejal, silinder, berukuran 6 m panjang dan diameter 8 cm. Sekiranya bar tertakluk kepada mampatan dengan menggunakan 90 beban.000 kg, cari:

a) Besarnya usaha mampatan di megapascal (MPA)

b) Berapa lama penurunan bar?

Penyelesaian kepada

Pertama adalah kawasan A bahagian silang bar, yang bergantung pada diameternya, menghasilkan:

A = π. D² / 4 = π. (0.08 m)² / 4 = 5.03 x 10^-3 m²

Kekuatan itu segera, melalui F = m.G = 90.000 kg x 9.8 m/s²= 882.000 n.

Akhirnya usaha purata dikira seperti berikut:

E = F/ A = 882.000 n/ 5.03 x 10^-3 m² = 1.75 x 10⁸ PA = 175 mpa

Penyelesaian b

Persamaan untuk usaha kini digunakan, mengetahui bahawa bahan itu mempunyai tindak balas elastik:

E = y. (Δ /l)

Modul muda keluli ditemui dalam Jadual 1:

δ = e.L / y = 6 m x 1.75 x 10⁸ PA / 200 x 10 ⁹ PA = 5.25 x 10 ^-3 M = 5.25 mm.

Rujukan

1. Bir, f. 2010. Bahan mekanik. 5th. Edisi. McGraw Hill.
2. Giancoli, d.  2006. Fizik: Prinsip dengan aplikasi. 6^Tth  Ed. Prentice Hall.
3. Hibbeler, R.C. 2006. Bahan mekanik. 6th. Edisi. Pendidikan Pearson.
4. Tippens, ms. 2011. Fizik: Konsep dan aplikasi. Edisi ke -7. McGraw Hill
5. Wikipedia. Tekanan (Mekanik). Pulih dari: wikipedia.org.