Formula konduktansi, pengiraan, contoh, latihan

The konduktansi Dari pemandu ia ditakrifkan sebagai kemudahan yang harus dilewatkan arus elektrik. Ia tidak hanya bergantung pada bahan yang digunakan untuk pembuatannya, tetapi juga pada geometrinya: panjang dan kawasan bahagian silang.

Simbol yang digunakan untuk konduktansi adalah G, dan terbalik rintangan elektrik r, magnitud yang lebih biasa. Unit Sistem Antarabangsa Jika untuk konduktansi adalah kebalikan dari Ohmio, dilambangkan sebagai Ω^-1 dan terima nama Siemens (S).

Rajah 1. Konduktansi bergantung pada bahan dan geometri pemandu. Sumber: Pixabay.

Istilah lain yang digunakan dalam elektrik, yang sama seperti konduktansi dan berkaitan adalah kekonduksian dan juga memandu, Tetapi mereka tidak boleh dikelirukan. Yang pertama dari istilah ini adalah harta intrinsik bahan yang mana pemandu dihasilkan dan yang kedua menerangkan aliran caj elektrik melaluinya.

Untuk konduktor elektrik dengan bahagian silang kawasan yang berterusan Ke, panjang L dan kekonduksian σ, Konduktansi diberikan oleh:

G = σ.KEPADA

Kepada kekonduksian yang lebih besar, konduktansi yang lebih besar. Juga, semakin besar kawasan keratan rentas, semakin mudah pemandu untuk membiarkan lulus semasa. Sebaliknya, semakin besar panjang l, semakin rendah konduktansi, kerana pembawa semasa kehilangan lebih banyak tenaga dalam perjalanan yang lebih lama.

[TOC]

Bagaimana konduktansi dikira?

Konduktansi g untuk konduktor dengan kawasan seksyen silang tetap dikira mengikut persamaan yang diberikan di atas. Ini penting, kerana jika bahagian silang tidak tetap, pengiraan integral mesti digunakan untuk mencari kedua -dua rintangan dan konduktansi.

Oleh kerana ia adalah kebalikan dari rintangan, konduktansi g dapat dikira mengetahui bahawa:

Boleh melayani anda: Model mekanikal kuantum atom

G = 1/r

Malah, rintangan elektrik pemandu dapat diukur secara langsung dengan multimeter, radas yang juga mengukur arus dan voltan.

Unit pemacu

Seperti yang dinyatakan pada mulanya, unit konduktansi dalam sistem antarabangsa adalah Siemens (s). Dikatakan bahawa pemandu mempunyai konduktansi 1 s jika arus yang melintasi ia meningkat sebanyak 1 amperio untuk setiap volt perbezaan potensial.

Mari lihat bagaimana mungkin melalui undang -undang Ohm, jika ditulis dari segi konduktansi:

V = i.R = i/g

Di mana V Ia adalah perbezaan voltan atau potensi antara hujung pemandu dan Yo Keamatan semasa. Dari segi magnitud ini formula tetap seperti ini:

G = i/v

Dahulu unit konduktansi adalah Mho (ohm ditulis ke belakang) dilambangkan sebagai ʊ, yang merupakan modal atau omega terbalik. Notasi ini tidak digunakan dan digantikan oleh Siemens Sebagai penghormatan kepada jurutera dan pencipta Jerman Ernst von Siemens (1816-1892), perintis telekomunikasi, tetapi kedua-duanya sama dengan.

1 mho = 1 siemens = 1 a/v (ampere/volt)

Rajah 2. Konduktansi berbanding rintangan. Sumber: Wikimedia Commons. Think Tank [CC oleh 3.0 (https: // creativeCommons.Org/lesen/oleh/3.0)]

Dalam sistem pengukuran lain, Statsiemens (statistik) (dalam sistem CGS atau sentimeter-gram-detik) dan Absiemens (abs) (Sistem CGS Elektromagnet) dengan "S" pada akhirnya, tanpa menunjukkan tunggal atau jamak, kerana mereka berasal dari nama yang betul.

Beberapa kesetaraan

1 statistik = 1.11265 x 10 ^-12 Siemens

1 abs = 1 x 10⁹ Siemens

Contoh

Seperti yang dinyatakan sebelum ini, mempunyai rintangan, konduktansi segera diketahui apabila menentukan nilai songsang atau timbal balik. Dengan cara ini rintangan elektrik 100 ohm bersamaan dengan 0.01 Siemens, sebagai contoh.

Di bawah dua lagi contoh penggunaan konduktansi:

Boleh melayani anda: kejutan magnet: unit, formula, pengiraan, contoh

Kekonduksian dan konduktansi

Mereka adalah istilah yang berbeza, seperti yang telah ditunjukkan. Kekonduksian adalah harta bahan yang dibuat oleh pemandu, sementara pemandu adalah tipikal pemandu.

Kekonduksian boleh dinyatakan dari segi g sebagai:

σ = g.(The)

Seterusnya, meja dengan kekonduksian bahan konduktif yang sering digunakan:

Jadual 1. Kekonduksian, ketahanan dan pekali haba beberapa konduktor. Suhu Rujukan: 20 ºC.

Logam	σ x 106 (Ye)	ρ x 10-8 (Ω.m)	α ºC-1
Perak	62.9	1.59	0.0058
Tembaga	56.5	1.77	0.0038
Emas	41.0	2.44	0.0034
Aluminium	35.4	2.82	0.0039
Tungsten	18.0	5.60	0.0045
Besi	10.0	10.0	0.0050

Rintangan selari

Apabila mereka mempunyai litar dengan rintangan selari, kadang -kadang perlu untuk mendapatkan rintangan yang setara. Mengetahui nilai rintangan yang setara membolehkan menggantikan set rintangan untuk satu nilai.

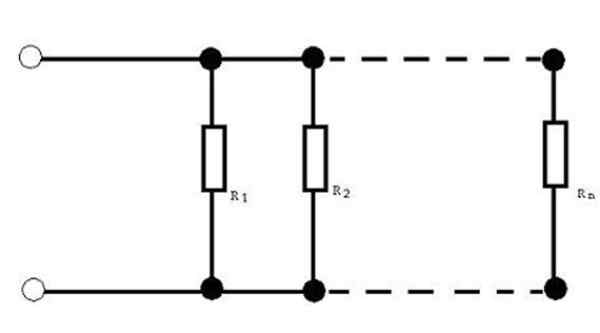Rajah 3. Persatuan rintangan selari. Sumber: Wikimedia Commons. Tiada pengarang yang boleh dibaca mesin yang disediakan. Sotake diasumsikan (berdasarkan tuntutan hak cipta). [CC BY-SA 3.0 (http: // creativeCommons.Org/lesen/by-sa/3.0/]].

Untuk konfigurasi rintangan ini, rintangan setara diberikan oleh:

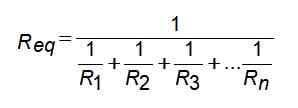
Tetapi jika anda menulis dari segi konduktansi, ia sangat dipermudahkan: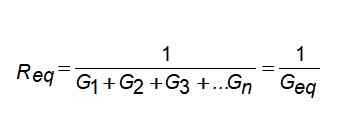Oleh itu:

G_Pers = G₁ + G₂ + G₃ +... g_n

Iaitu, konduktansi bersamaan adalah jumlah konduktans. Sekiranya anda ingin mengetahui rintangan yang setara, hasilnya hanya dilaburkan.

Latihan

- Latihan 1

a) Tulis undang -undang ohm dari segi konduktansi.

b) Cari konduktansi dawai 5 tungsten sebanyak 5.Panjang 4 cm dan 0.Diameter 15 mm.

c) Sekarang arus 1 diluluskan.5 A untuk wayar. Apakah perbezaan potensi antara hujung pemandu ini?

Boleh melayani anda: 31 jenis daya dalam fizik dan ciri mereka

Penyelesaian kepada

Dari bahagian sebelumnya yang anda perlu:

V = i/g

G = σ.KEPADA

Menggantikan yang terakhir, ia tetap seperti ini:

V = i /(σ.A/l) = i.L / σ.Ke

Di mana:

-Saya adalah intensiti semasa.

-L adalah panjang pemandu.

-σ adalah kekonduksian.

-A adalah kawasan bahagian silang.

Penyelesaian b

Untuk mengira konduktansi dawai tungsten ini, kekonduksiannya diperlukan, yang terdapat dalam Jadual 1:

σ = 18 x10⁶ Ye

L = 5.4 cm = 5.4 x 10^-2 m

D = 0. 15 mm = 0.15 x 10^-3 m

A = π.D² / 4 = π . (0.15 x 10^-3 m)² / 4 = 1.77 x 10^-8 m²

Menggantikan persamaan yang anda ada:

G = σ.A/l = 18 x10⁶ Ye . 1.77 x 10^-8 m² / 0.15 x 10^-3 M = 2120.6 s.

Penyelesaian c

V = i/g = 1.5 a / 2120.6 s = 0.71 mv.

- Latihan 2

Cari rintangan bersamaan dalam litar berikut dan mengetahui bahawa saya_{Sama ada} = 2 a, hitung i_x dan kuasa yang hilang oleh litar:

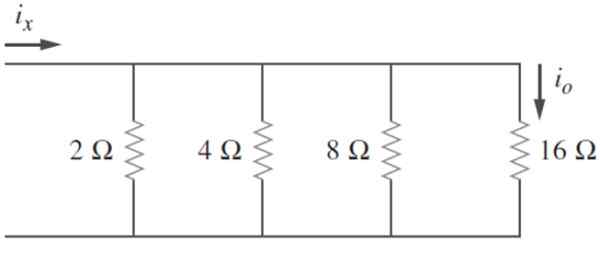Rajah 4. Litar dengan rintangan selari. Sumber: Alexander, C. 2006. Asas Litar Elektrik. Ke -3. Edisi. McGraw Hill.

Penyelesaian

Rintangan disenaraikan: r₁= 2 Ω; R₂= 4 Ω; R₃= 8 Ω; R₄= 16 Ω

Konduktansi kemudian dikira dalam setiap kes: g₁ = 0.5 ʊ; G₂ = 0.25 ʊ; G₃ = 0.125 ʊ; G₄ = 0.0625 ʊ

Dan akhirnya mereka menambah seperti yang ditunjukkan sebelum ini, untuk mencari konduktansi yang setara:

G_Pers = G₁ + G₂ + G₃ +... g_n = 0.5 ʊ + 0.25 ʊ + 0.125 ʊ + 0.0625 ʊ = 0.9375 ʊ

Oleh itu r_Pers = 1.07 Ω.

Voltan dalam r₄ adalah v₄ = i_{Sama ada}. R₄ = 2 a . 16 Ω = 32 V, dan sama untuk semua rintangan, kerana ia disambungkan selari. Maka ada kemungkinan untuk mencari arus yang beredar untuk setiap rintangan:

-Yo₁ = V₁ /R₁ = 32 v / 2 Ω = 16 a

-Yo₂ = V₂ /R₂ = 32 v / 4 Ω = 8 a

-Yo₃ = V₃ /R₃ = 32 v / 8 Ω = 4 a

-Yo_x = i₁ +  Yo₂ +  Yo₃ + Yo_{Sama ada} = 16 + 8 + 4 + 2 a = 30 a

Akhirnya, kuasa yang hilang P ialah:

P = (i_x)². R_Pers = 30 hingga x 1.07 Ω = 32.1 w

Rujukan

1. Alexander, c. 2006. Asas Litar Elektrik. Ke -3. Edisi. McGraw Hill.
2. Megaerpere / millivolt ke penukaran kalkulator absiemen. Pulih dari: Pinkbird.org.
3. Garcia, l. 2014. Elektromagnetisme. 2. Edisi. Universiti Perindustrian Santander. Colombia.
4. Knight, r.  2017. Fizik untuk saintis dan kejuruteraan: Pendekatan Strategi.  Pearson.
5. Roller, d. 1990. Fizikal. Elektrik, magnet dan optik. Jilid II. Editorial kembali.
6. Wikipedia. Konduktansi elektrik. Pulih dari: Adakah.Wikipedia.org.
7. Wikipedia. Siemens. Pulih dari: Adakah.Wikipedia.org.