Koordinat Rectangular Contoh dan Latihan Diselesaikan

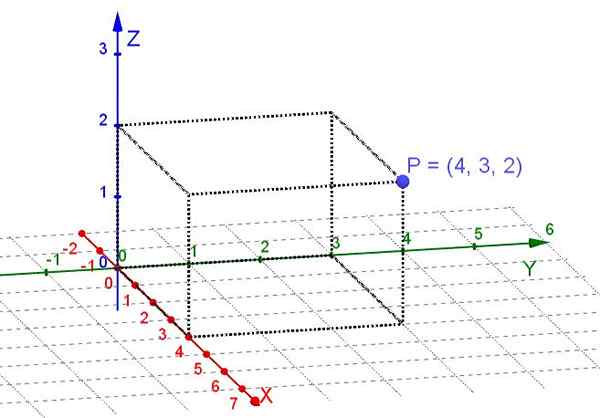
The Koordinat segi empat tepat o Cartesian adalah yang diperolehi apabila diproyeksikan secara ortogonal pada tiga paksi Cartesian x, y, z titik yang terletak di ruang tiga dimensi.

Paksi Cartesian saling berorientasikan tegak lurus. Dalam sistem koordinat Cartesian, tiga nombor sebenar yang merupakan koordinat segi empat tepat diberikan kepada setiap titik di ruang angkasa.

Rajah 1. Koordinat Rectangular Point P (Penghuraian Sendiri)

Pesawat adalah subspace ruang tiga dimensi. Sekiranya mempertimbangkan mata di atas kapal terbang, sudah cukup untuk memilih sepasang paksi serenjang x, dan sebagai sistem Cartesian. Kemudian pada setiap titik di atas kapal terbang dua nombor nyata diberikan kepadanya bahawa koordinat segi empat tepatnya.

[TOC]

Asal koordinat segi empat tepat

Koordinat segi empat tepat pada asalnya dicadangkan oleh ahli matematik Perancis René Descartes (1596 dan 1650), itulah sebabnya mereka menerima denominasi Cartesia.

Dengan idea Descartes ini, titik -titik satah dan ruang diberikan nombor, supaya angka geometri telah mengaitkan persamaan algebra dan teorem geometri klasik dapat ditunjukkan secara algebra. Dengan koordinat Cartesian, geometri analisis dilahirkan.

Pesawat Cartesian

Jika pada satah dua garis tegak lurus dipilih yang bersilang pada satu titik atau; dan jika juga setiap baris diberikan arah dan skala berangka antara titik -titik yang sama berturut -turut, maka ada sistem atau pelan Cartesian di mana setiap titik satah dikaitkan dengan pasangan yang teratur dari dua nombor nyata yang masing -masing unjurannya masing -masing di paksi x dan y.

Mata a = (3, 2); B = (-2, 3); C = (-2, -3) dan d = (3, -3) diwakili dalam pesawat Cartesian seperti yang ditunjukkan di bawah:

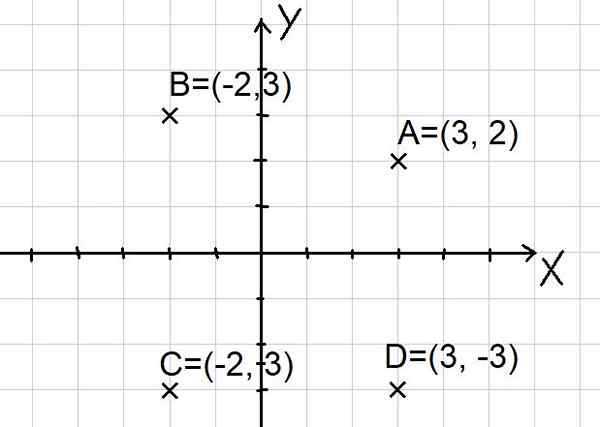Rajah 2. Mata pada pesawat Cartesian. (Huraian sendiri)

Perhatikan bahawa dua paksi x dan y membahagikan pesawat ke dalam empat sektor yang dipanggil kuadran. Point A berada di kuadran pertama, B dalam kuadran kedua, C di kuadran ketiga dan titik D di kuadran keempat.

Boleh melayani anda: penduduk dan sampel

Jarak antara dua mata

Jarak antara dua mata a dan b pesawat Cartesian adalah panjang segmen yang menyatukannya. Jarak ini boleh dikira secara analitik seperti berikut:

D (a, b) = √ (bx - ax)^2 + (oleh - ay)^2)

Formula anterior diperoleh dengan menggunakan teorem pythagoras.

Memohon formula tersebut kepada titik A, b Rajah 2 adalah:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

Iaitu, D (A, B) = 5.10 unit. Perhatikan bahawa jarak diperoleh tanpa perlu mengukur dengan peraturan, prosedur algebra sepenuhnya telah diikuti.

Ekspresi analisis garis

Koordinat Rectangular membolehkan perwakilan analisis objek geometri asas seperti titik dan garis. Dua mata a dan b menentukan satu baris. Cerun garis ditakrifkan sebagai kuota antara perbezaan koordinat dan titik b kurang, dibahagikan dengan perbezaan dalam koordinat x titik b kurang A:

menunggu = (oleh - ay)/(bx - kapak)

Sebarang titik koordinat (x, y) yang dimiliki oleh garis (ab) mesti mempunyai cerun yang sama:

menunggu = (y - ay)/(x - kapak)

Persamaan yang diperolehi oleh kesamaan lereng adalah perwakilan analitik atau algebra garis yang melewati titik A dan B:

(y - ay)/(x - ax) = (oleh - ay)/(bx - ax).

Jika anda diambil untuk a dan b koordinat segi empat tepat Rajah 2 adalah:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

Dalam kes ini terdapat garis dengan cerun negatif -⅕, yang bermaksud yang terletak pada titik garis dan meningkatkan koordinat x dalam satu unit, koordinat dan berkurangan dalam 0.2 unit. 

Boleh melayani anda: Toroid atau Toro Dona

Cara paling biasa untuk menulis persamaan garis dalam satah adalah dengan koordinat dan jelas sebagai fungsi pembolehubah x:

y = -(1/5) x + 13/5 

Contoh

Contoh 1

Dapatkan dengan kaedah analisis jarak antara titik C dan A, sebagai koordinat segi empat tepat c = (-2, -3) dan yang A = (3.2).

Formula jarak Euclidean antara kedua -dua titik ini ditulis seperti ini:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Menggantikan koordinat segi empat tepatnya yang anda miliki:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7.07

Contoh 2

Dapatkan persamaan garis yang melewati titik C koordinat (-2, -3) dan titik P koordinat (2, 0).

Pertama, cerun garis CP diperolehi:

menunggu = (0 -(-3)) / (2 -( -2)) = ¾ 

Satu titik q dari koordinat segi empat tepat generik (x, y) yang dimiliki oleh garis CP mesti mempunyai cerun yang sama:

menunggu = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

Iaitu persamaan garis CP adalah:

(Y +3) / (x +2) = ¾

Cara alternatif untuk menulis persamaan garis CP adalah penjelasan dan:

y = ¾ x - 3/2 

Latihan yang diselesaikan

Latihan 1

Dapatkan koordinat segi empat tepat titik persimpangan antara garis y = - (1/5) x + 13/5 dan garis y = ¾ x - 3/2.

Penyelesaian: Dengan definisi, titik persimpangan kedua -dua baris berkongsi koordinat segi empat tepat yang sama. Oleh itu, koordinat dan pada titik persimpangan adalah sama untuk kedua -dua baris:

-(1/5) x + 13/5 = ¾ x - 3/2

Apa yang membawa kepada ungkapan berikut:

Boleh melayani anda: trapezoid segi empat tepat: sifat, hubungan dan formula, contoh

(¾ + ⅕) x = 13/5 +3/2

Menyelesaikan jumlah pecahan diperoleh:

19/20 x = 41/10

Membersihkan x:

x = 82/19 = 4.32

Untuk mendapatkan nilai dan persimpangan, nilai x yang diperolehi dalam salah satu baris diganti:

y = ¾ 4.32 - 3/2 = 1.74

Ini bermakna bahawa garis yang diberikan dipintas pada titik I koordinat i = (4.32; 1,74).

Latihan 2

Dapatkan persamaan lilitan yang melewati titik koordinat segi empat tepat r (3, 4) dan yang mempunyai pusat pada asal koordinat.

Penyelesaian: Radio R adalah jarak dari titik r ke asal atau koordinat (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Iaitu, ia adalah Radius 5 Circle 5 yang berpusat pada (0.0).

Mana -mana titik p (x, y) dari lilitan mesti mempunyai jarak yang sama 5 ke pusat (0, 0) untuk apa yang boleh ditulis:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

Iaitu:

√ (x^2 + y^2) = 5

Untuk menghapuskan akar kuadrat, kedua -dua anggota kesamaan dibiarkan secara senyap -senyap:

x^2 + y^2 = 25

Apakah persamaan lilitan.

Dengan contoh ini, kuasa sistem koordinat segi empat tepat digambarkan, yang membolehkan untuk menentukan objek geometri, seperti lilitan tanpa perlu menggunakan kertas, pensil dan kompas. Lilitan yang diminta hanya oleh kaedah algebra telah ditentukan.

Rujukan

1. Arfken G dan Weber H. (2012). Kaedah matematik untuk ahli fizik. Panduan komprehensif. Edisi ke -7. Akhbar Akademik. ISBN 978-0-12-384654-9
2. Pengiraan CC. Koordinat segi empat tepat menyelesaikan masalah. Pulih dari: pengiraan.DC
3. Weisstein, Eric W. "Koordinat Cartesian."Dari Mathworld-A Wolfram Web. Pulih dari: Mathworld.Wolfram.com
4. Wikipedia. Sistem koordinat Cartesian. Diperoleh dari: dalam.Wikipedia.com