Kriteria segitiga yang sama

Apakah kriteria persamaan segitiga?

Kriteria persamaan segitiga adalah peraturan yang membolehkan mengetahui jika dua segitiga serupa. Kesamaan angka geometri, termasuk segitiga, memerlukan angka mempunyai cara yang sama, walaupun mereka tidak semestinya mempunyai saiz yang sama atau orientasi yang sama.

Bagi dua segitiga yang sama, perlu: i) sisi homolog mereka berkadar dan ii) sudut dalaman masing -masing mempunyai ukuran yang sama.

Rajah 1. Dua segitiga yang sama: walaupun mereka tidak mempunyai saiz yang sama, sisi mereka berkadar dan sudut dalaman mereka mempunyai ukuran yang sama. Sumber: f. Zapata.

Nisbah atau perkadaran berkadar antara dua jumlah A dan B diwakili oleh nisbah A/B, dengan B ≠ 0. Untuk segitiga yang sama, perkadaran berikut antara pihak mereka adalah sah:

a/a '= b/b' = c/c '= r

Nilai r dipanggil sebab persamaan.

Di samping itu, sudut dalaman yang sepadan harus mempunyai ukuran yang sama, oleh itu: ∠A = ∠A '; ∠B = ∠B 'dan ∠C = ∠C'. Mengikut syarat -syarat ini, kriteria persamaan segitiga adalah:

Kriteria 1: Dua segitiga adalah serupa jika mereka mempunyai dua sudut dalaman yang sama. Jika ya, sudut ketiga juga mengukur perkara yang sama, kerana jumlah sudut dalaman di mana -mana segitiga adalah 180º:

α = α '; β = β '

Kriteria 2: Segitiga adalah sama jika dua sisi homolog adalah berkadar dan sudut di antara mereka adalah sama:

a/a '= b/b'; α = α '

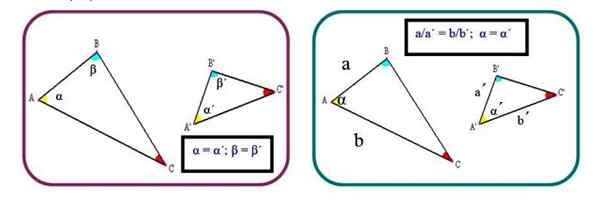Rajah 2. Dua kriteria untuk mewujudkan persamaan segitiga. Sumber: f. Zapata.

Kriteria 3: Ketiga -tiga pihak homolog adalah berkadar:

a/a '= b/b' = c/c '= r

Contoh

Persamaan segitiga sangat berguna untuk mengira ketinggian dan jarak yang tidak mudah diukur secara langsung. Melalui beberapa pengiraan mudah, adalah mungkin untuk mengetahui panjang ini dengan membandingkan segitiga yang serupa.

Boleh melayani anda: Teorem asas aritmetik: demonstrasi, aplikasi, latihan

Ketinggian lajur, bangunan dan pokok

Dikatakan bahawa bapa geometri di Yunani kuno, seperti Miletus (625-547 hingga.C.), mengira ketinggian lajur kuil tanpa memerlukan instrumen khas, hanya membandingkan panjang bayang -bayang tongkatnya dengan lajur dan menggunakan persamaan segitiga. Dengan kaedah yang sama dia berjaya mengukur ketinggian piramid besar Mesir dan dengan itu menarik perhatian Firaun.

Jarak ke bulan

Terdapat percubaan mudah yang dilakukan untuk mengira jarak antara bumi dan bulan. Ia memerlukan mata wang, sedikit pita pelekat dan vernier atau peraturan siswazah. Apabila bulan penuh, mata wang dilampirkan pada segelas tingkap dan bulan diperhatikan dengan satu mata, terletak sedemikian rupa sehingga mata wang meliputi hanya bulan purnama.

Apabila ini berlaku, sebab antara diameter mata wang dan jarak antara mata dan mata wang, adalah sama ada di antara diameter bulan dan jarak antara mata dan bulan:

Diameter mata wang/mata wang jarak = diameter bulan/jarak ke bulan

Sebabnya lebih kurang 1/110. Yang bermaksud bahawa jarak ke bulan adalah 110 kali diameter ini.

Pada masa ini jejari bulan dianggarkan pada tahun 1737.1 km, jadi diameternya adalah 3474.2 km. Dengan menggantikan nilai ini dalam hubungan:

Jarak ke bulan = diameter bulan ÷ (diameter mata wang/jarak ke mata wang)

Diperoleh:

Jarak ke bulan = 3474.2 km ÷ (1/110) = 382.162 km

Ia dapat melayani anda: prisma hepagon

Sangat dekat dengan nilai yang ditubuhkan oleh 384 ahli astronomi.000 km.

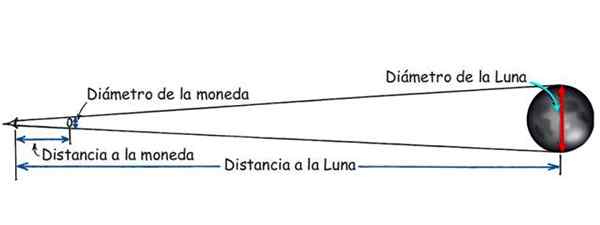Rajah 3. Jarak ke bulan dapat diketahui terima kasih kepada persamaan segitiga. Sumber: Modified Hewitt, P. Fizik Konsep.

Jarak antara kapal dan pantai

Untuk mengukur jarak antara kapal dan pantai, kepentingan terjebak di pantai di mata A, B, C dan Q. Segitiga ABC dan PCQ adalah serupa dengan kriteria 1, kerana mereka mempunyai dua sudut yang sama: dua sudut ∠C = α yang ditentang oleh puncak dan dua sudut lurus sama dengan 90º: ∠B = ∠Q.

Dua segitiga yang terletak dengan cara ini dikatakan masuk Kedudukan Thales Dan mereka selalu serupa. Segitiga dikenal pasti dalam kedudukan Thales kerana mempunyai sudut yang sama dan sisi yang bertentangan pada sudut itu selari.

Di bahagian seterusnya terdapat latihan dengan nilai berangka.

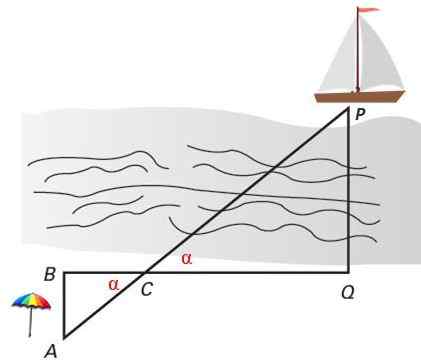Rajah 4. Dua segitiga yang serupa di kedudukan Thales berfungsi untuk mengira jarak tegak lurus kapal ke pantai. Sumber: f. Zapata.

Latihan yang diselesaikan

Latihan 1

Anda ingin mengetahui sejauh mana kapal layar itu berlabuh dalam angka sebelumnya, dari titik yang terletak di tepi pantai, yang mana kepentingan dipaku di titik A, B, C dan Q, dengan itu menentukan segitiga ABC, yang mana sama dengan PCQ, tetapi sisinya lebih mudah diukur.

Kirakan PQ jarak tegak lurus antara kapal dan pantai, dengan persamaan segitiga, jika jarak yang tersedia adalah:

AB = 12 m

BC = 16 m

Qc = 60 m

Penyelesaian

Perkadaran antara pihak homolog adalah:

AB/QP = BC/CQ = 16 m/60 m = 0.267

Oleh itu 0.267 adalah sebab persamaan:

AB/QP = 0.267

Qp = ab / 0.267 = 12 m / 0.267 = 44.9 m

Latihan 2

Dalam segitiga berikut: Berapa banyak langkah segmen iklan?

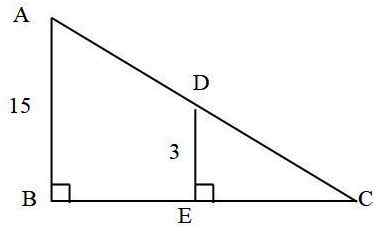
Diketahui bahawa:

• AC = 25 cm
• AB = 15 cm
• DE = 3 cm

Boleh melayani anda: gandaan 2: apa dan penjelasan

Penyelesaian

Segitiga adalah serupa, kerana mereka berkongsi sudut iaitu ∠C dan sisi dan ab selari. Nisbah kesamaan dikira oleh:

R = ab / de = 15 cm / 3 cm = 5

Dan juga melalui:

R = ac / dc

Oleh itu dc = ac / r = 25 cm / 5 = 5 cm

Sejak:

Ac = ad + dc

Ia mengikuti bahawa AD = AC - DC = 25 cm - 5 cm = 20 cm

Latihan 3

Segitiga isosceles mempunyai perimeter 49 cm dan pangkalan 21 cm. Kirakan perimeter segitiga yang serupa dengan ini, tetapi asasnya mengukur 4 cm.

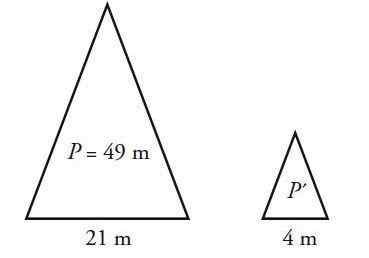
Penyelesaian

Segitiga isosceles mempunyai dua sisi yang sama, berbeza dengan asas b. Biarkan ℓ ukuran sisi dan p perimeter, yang terdiri daripada jumlah tiga sisi. Untuk segitiga terbesar:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Sekarang perkadaran antara sisi segitiga dibesarkan, segitiga kecil dilambangkan dengan premium:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Perimeter segitiga kecil akan:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Rujukan

1. Alexander, d. 2013. Geometri. 5th. Edisi. Pembelajaran Cengage.
2. Hewitt, Paul. 2012. Sains Fizikal Konsep. 5th. Ed. Pearson.
3. Clemens, s. Geometri dengan aplikasi. Addison Wesley.
4. Ibáñez, ms. 2010. Matematik III. Pembelajaran Cengage.
5. Jiménez, r. Matematik II: Geometri dan Trigonometri. 2. Edisi. Pearson.
6. Stewart, J. 2007. Precalculation. 5th. Edisi. Pembelajaran Cengage.
7. Vicmat. Samos Aristarco: Langkah Sistem Suria. Pulih dari: vicmat.com