Unsur segi empat, sifat, klasifikasi, contoh

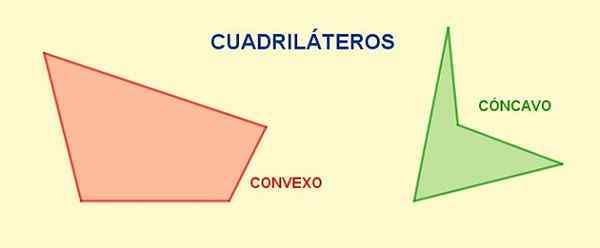
A Quadrilateral Ia adalah poligon empat dan empat titik. Mereka sisi bertentangan Mereka adalah mereka yang tidak mempunyai simpul biasa, semasa mereka sisi berturut -turut Mereka yang mempunyai puncak biasa.

Dalam segi empat segi mereka sudut bersebelahan Mereka yang berkongsi sisi, sementara Sudut bertentangan Mereka tidak mempunyai sisi biasa. Satu lagi ciri penting dalam segi empat adalah bahawa jumlah empat Sudut dalaman Ia adalah dua kali sudut rata, iaitu 360º atau 2π radians.

Rajah 1. Pelbagai kuadrilaterals. Sumber: f. Zapata.

Diagonal Mereka adalah segmen yang menyatukan puncak dengan sebaliknya dan dalam cincin tertentu, dari setiap puncak anda boleh melukis satu pepenjuru. Jumlah bilangan pepenjuru segi empat adalah dua.

Quadrilaterals adalah angka yang diketahui oleh manusia sejak zaman purba. Rekod arkeologi, serta pembinaan yang bertahan hari ini, membuktikannya.

Juga hari ini kuadrilateral terus mempunyai kehadiran penting dalam kehidupan seharian. Pembaca dapat menemui borang ini di skrin di mana teks dibaca pada saat yang tepat ini, di tingkap, pintu, bahagian automotif dan tempat yang tidak terhitung banyak lagi.

[TOC]

Klasifikasi Quadrilaterals

Menurut paralelisme sisi yang bertentangan, kuadrilaterals diklasifikasikan seperti berikut:

1. Trapezoid, Apabila tidak ada paralelisme dan segi empat.
2. Trapeze, Apabila terdapat paralelisme antara sepasang sisi bertentangan.
3. Parallelogram, Apabila sisi bertentangan mereka selari dua hingga dua.

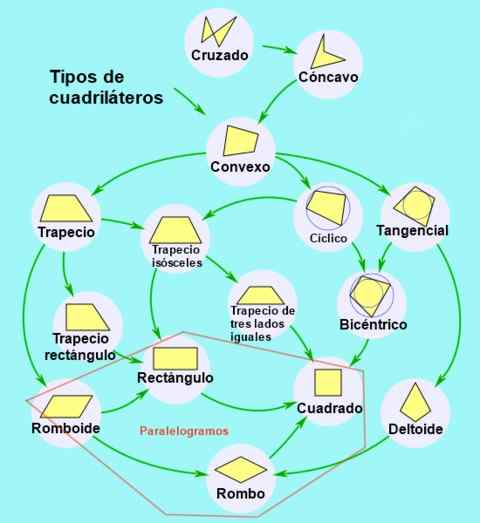Rajah 2. Klasifikasi dan Subklasifikasi Quadrilaterals. Sumber: Wikimedia Commons.

Jenis Parallelogram

Sebaliknya, paralelogram boleh diklasifikasikan mengikut sudut dan sisi mereka seperti berikut:

1. Rectangle, Ia adalah selaras yang mempunyai empat sudut dalaman yang sama dengan ukuran. Sudut dalaman segi empat tepat membentuk sudut kanan (90º).
2. Dataran, Ia adalah segi empat tepat dengan empat sisi ukuran yang sama.
3. Berlian, Ia adalah selaras dengan empat sisi, tetapi sudut bersebelahan yang berbeza.
4. Rhomboid, paralelogram dengan sudut bersebelahan yang berbeza.

Trapeze

Trapeze adalah segi empat cembung dengan dua sisi selari.

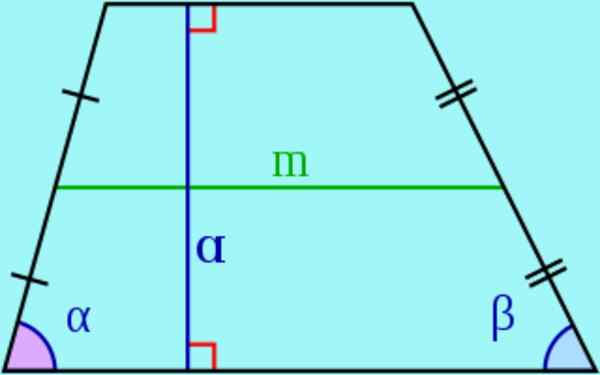Rajah 3. Pangkalan, sisi, ketinggian dan median trapeze. Sumber: Wikimedia Commons.

- Dalam trapeze sisi selari dipanggil pangkalan Dan bukan parallel dipanggil sisi.

- The ketinggian trapeze adalah jarak antara kedua -dua pangkalan, iaitu, panjang segmen dengan hujung di pangkalan dan tegak lurus dengan yang sama. Segmen ini juga dipanggil ketinggian trapeze.

- The median Ia adalah segmen yang bergabung dengan titik tengah di sisi. Ia dapat ditunjukkan bahawa median selari dengan pangkalan trapeze dan panjangnya sama dengan separuh -kotak pangkalan.

- Kawasan trapeze adalah ketinggiannya yang didarabkan oleh separa -bodi pangkalan:

Kawasan trapeze = ketinggian * (asas 1 + asas 2) / 2

Jenis trapeze

-Trapeze Rectangle: Ia adalah yang mempunyai sisi tegak lurus ke pangkalan. Sebelah ini juga ketinggian trapezoid.

-Trapezium isosceles: Yang mempunyai sisi panjang yang sama. Dalam trapezoid isosceles sudut bersebelahan dengan pangkalannya sama.

-Escaleno Trapezio: Orang yang mempunyai sisi panjang yang berbeza. Sudutnya yang bertentangan boleh menjadi akut dan bodoh yang lain, tetapi ia juga boleh berlaku bahawa kedua -duanya adalah bodoh atau kedua -duanya akut.

Boleh melayani anda: Latihan pemfaktoran yang diselesaikan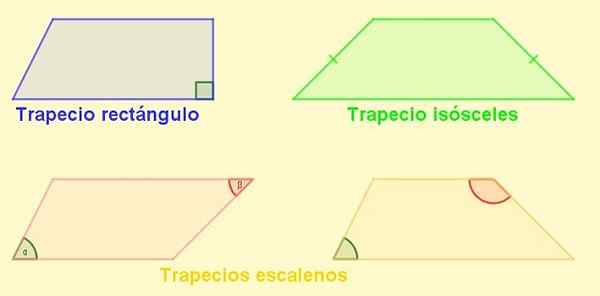 Rajah 4. Jenis trapeze. Sumber: f. Zapata.

Parallelogram

Parallelogram adalah segi empat segi yang sebaliknya adalah selari dua hingga dua. Dalam paralelogram sudut bertentangan adalah sama dan sudut bersebelahan adalah tambahan, atau dengan kata lain, sudut bersebelahan berjumlah 180º.

Sekiranya paralelogram mempunyai sudut yang betul, maka semua sudut lain juga akan dan angka yang dihasilkan dipanggil Rectangle. Tetapi jika segi empat tepat juga mempunyai sisi bersebelahan dengan panjang yang sama, maka semua sisinya sama dan angka yang dihasilkan adalah Dataran.

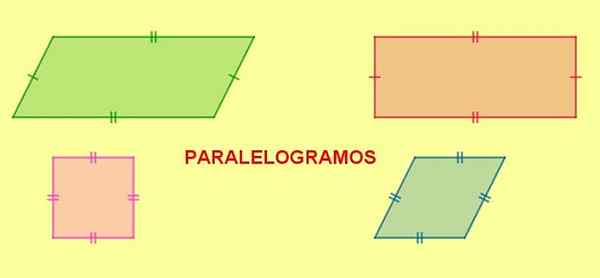Rajah 5. Parallelograms. Segi empat tepat, persegi dan rhombus adalah paralelogram. Sumber: f. Zapata.

Apabila selaras mempunyai dua sisi bersebelahan dengan panjang yang sama, semua sisinya akan menjadi panjang yang sama dan angka yang dihasilkan adalah berlian.

Ketinggian paralelogram adalah segmen dengan hujung di sisi yang bertentangan dan tegak lurus kepada mereka.

Kawasan paralelogram

Kawasan paralelogram adalah produk asas dengan ketinggiannya, asasnya menjadi sisi tegak lurus ke ketinggian (Rajah 6).

Kawasan paralelogram = asas x ketinggian = a . h

Diagonals dari juru bicara

Dataran pepenjuru yang bermula dari puncak adalah sama dengan jumlah kuadrat kedua -dua belah pihak bersebelahan dengan titik tersebut lebih banyak produk ganda dari sisi -sisi oleh kosinus sudut titik itu:

F² = a² +  d² + 2 A D COS (α)

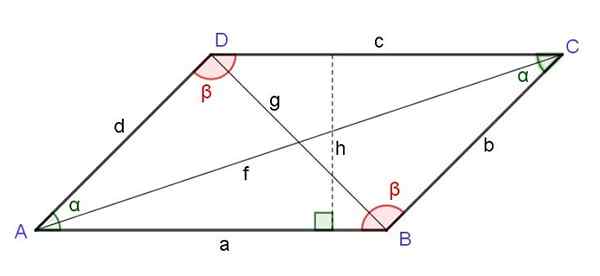Rajah 6. Parallelogram. Sudut bertentangan, ketinggian, pepenjuru. Sumber: f. Zapata.

Dataran pepenjuru yang bertentangan dengan puncak paralelogram adalah sama dengan jumlah kuadrat kedua -dua belah pihak bersebelahan dengan puncak tersebut dan menolak produk berganda dari sisi -sisi oleh kosinus sudut puncak itu:

g² = a² + d² - 2 A D COS (α)

Undang -undang Parallelograms

Dalam mana -mana paralelogram, jumlah kotak di sisi mereka adalah sama dengan jumlah kuadrat diagonal:

ke² + b² + c² + d² = f² + g²

Rectangle

Rectangle adalah segi empat segi dengan sisi bertentangan selari dua hingga dua dan itu juga mempunyai sudut yang betul. Iaitu segi empat tepat adalah jenis paralelogram dengan sudut yang betul. Kerana menjadi paralelogram, Rectangle mempunyai sisi bertentangan dengan panjang sama a = c dan b = d = d. 

Tetapi seperti mana -mana sudut selari bersebelahan adalah tambahan dan sudut bertentangan yang sama, dalam segi empat tepat dengan mempunyai sudut yang betul, ia semestinya akan membentuk sudut lurus di tiga sudut yang lain. Iaitu Dalam segi empat tepat semua sudut dalaman mengukur 90º atau π/2 radians.

Diagonal dari segi empat tepat

Dalam segi empat tepat pepenjuru adalah panjang yang sama, Seperti yang akan ditunjukkan di bawah. Alasannya adalah seperti berikut; Rectangle adalah selaras dengan semua sudut lurus dan itulah sebabnya ia mewarisi semua sifat paralelogram, termasuk formula yang memberikan panjang pepenjuru:

F² = a²+  d² + 2 A D COS (α)

g² = a² + d² - 2 A D COS (α)

dengan α = 90º

Sebagai Cos (90º) = 0, Jadi ia berlaku:

F² = g² = a² +  d²

Itu dia f = g, dan oleh itu panjangnya F dan g Daripada kedua -dua pepenjuru segi empat tepat mereka sama dan panjangnya diberikan oleh:

Panjang pepenjuru segi empat tepat = √ (a² + b²)

Di samping itu, jika dalam segi empat tepat di sisi bersebelahan ke dan b Satu sisi didasarkan pada sisi lain akan ketinggian dan akibatnya kawasan segi empat akan menjadi:

Ia boleh melayani anda: Siri Fibonacci: Hartanah, Hubungan Semula Jadi, Aplikasi

Kawasan segi empat tepat = x b.

Perimeter adalah jumlah semua sisi segi empat tepat, tetapi sebagai bertentangan adalah sama, maka perlu untuk segi empat tepat sisi ke dan b Perimeter diberikan oleh formula berikut:

Perimeter segi empat tepat = 2 (a + b)

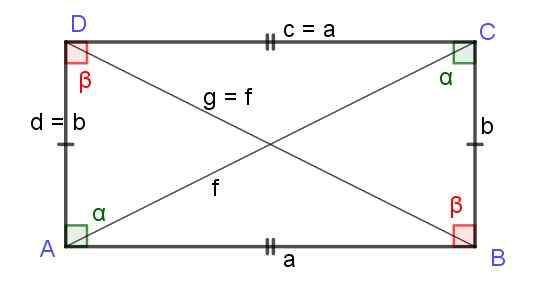Rajah 7. Segi empat tepat sisi a dan b. Pepenjuru f dan g adalah panjang yang sama. Sumber: f. Zapata.

Dataran

Dataran adalah segi empat tepat dengan sisi bersebelahan dengan panjang yang sama. Sekiranya dataran mempunyai sisi ke, Kemudian pepenjurunya F dan g Mereka mempunyai panjang yang sama, iaitu F = g = (√2) a.

Kawasan persegi adalah bahagiannya ditinggikan ke dataran:

Kawasan persegi = a²

Perimeter persegi adalah dua kali sisi:

Perimeter persegi = 4 a

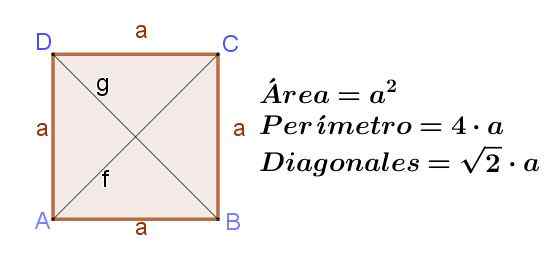Rajah 8. Persegi ke sisi A, menunjukkan kawasannya, perimeternya dan panjang pepenjuru. Sumber: f. Zapata ..

Berlian

Rhombus adalah paralelogram dengan sisi bersebelahan dengan panjang yang sama, tetapi seperti dalam parallelogram, sisi bertentangan adalah sama ketika itu, Semua sisi rombus adalah panjang yang sama.

Diagonal rombus adalah panjang yang berbeza, tetapi mereka dipotong pada sudut tepat.

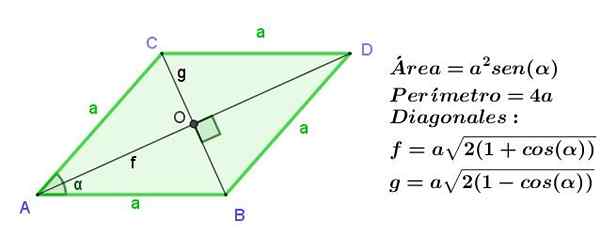Rajah 9. Rhombus dari sisi A, menunjukkan kawasan, perimeter dan panjang pepenjuru. Sumber: f. Zapata.

Contoh

Contoh 1

Menunjukkan bahawa dalam segi empat (tidak diseberang) sudut dalaman berjumlah 360º.

Rajah 10: Ia ditunjukkan sebagai jumlah sudut quadrilateral menambah 360º. Sumber: f. Zapata.

ABCD dianggap ABCD (lihat Rajah 10) dan BD pepenjuru ditarik. Dua Segitiga ABD dan BCD terbentuk. Jumlah sudut dalaman Segitiga Abd adalah:

α + β₁ + δ₁ = 180º

Dan jumlah sudut dalaman segitiga BCD adalah:

 β2 + γ + δ₂ = 180º

Menambah kedua -dua persamaan diperoleh:

α + β₁ + δ₁ +  β₂ + γ + δ₂ = 180º + 180º

Pengumpulan:

α + (β₁ +  β₂) + (δ₁ + δ₂) + γ = 2* 180º

Pengumpulan dan penolakan, akhirnya menunjukkan bahawa:

α + β + δ + γ = 360º

Contoh 2

Tunjukkan bahawa median trapezoid selari dengan pangkalannya dan panjangnya adalah separuh daripada pangkalan.

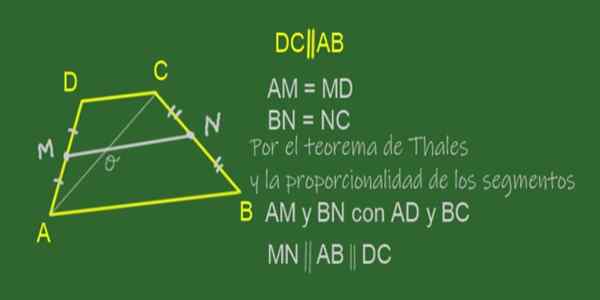Rajah 11. Median mn trapeze ABCD. Sumber: f. Zapata.

Median trapeze adalah segmen yang bergabung dengan titik tengahnya, iaitu, sisi bukan persamaan. Dalam trapeze ABCD yang ditunjukkan dalam Rajah 11 median adalah MN. 

Kerana ia adalah titik tengah titik AD dan N pertengahan BC, ia dipenuhi bahawa kuota AM / AD dan BN / BC sama.

Iaitu, AM adalah berkadar dengan Bn dalam perkadaran yang sama seperti AD adalah BC, jadi syarat -syarat untuk pemakaian teorem (timbal balik) Thales yang mengesahkan perkara berikut:

"Sekiranya dalam tiga atau lebih lurus dipotong oleh dua secant".

Dalam kes kita, disimpulkan bahawa garis Mn, Ab dan Dc selari antara satu sama lain, oleh itu:

"LDalam median salah satu trapeze selari dengan pangkalannya".

Boleh melayani anda: Operasi gabungan

Sekarang teorem Thales akan dikenakan:

"Satu set persamaan yang dipotong oleh dua atau lebih pengeringan menentukan segmen berkadar".

Dalam kes kami AD = 2 pagi, AC = 2 AO, jadi segitiga DAC serupa dengan segitiga MAO, dan akibatnya DC = 2 mo.

Hujah yang sama membolehkan untuk mengesahkan bahawa Cu adalah serupa dengan Con, di mana Ca = 2 Co dan Cb = 2 Cn. Ia mengikuti ab = 2 pada.

Pendek kata, AB = 2 pada y 2 mo. Oleh itu, apabila kita pergi:

Ab + dc = 2 pada + 2 mo = 2 (mo + on) = 2 mn

Akhirnya membersihkan MN:

Mn = (ab + dc) /2

Dan disimpulkan bahawa median trapezoid mengukur separa -bodi asas, atau dengan kata lain: median mengukur jumlah pangkalan, dibahagikan dengan dua.

Contoh 3

Menunjukkan bahawa dalam rombus pepenjuru dipotong pada sudut yang betul.

Rajah 12. Rhombus dan demonstrasi bahawa pepenjuru mereka dipotong pada sudut yang betul. Sumber: f. Zapata.

Lembaga Rajah 12 menunjukkan pembinaan yang diperlukan. Pertama, selaras ABCD ditarik dengan AB = BC, itu adalah rhombus. Diagonal AC dan DB menentukan lapan sudut yang ditunjukkan dalam angka tersebut.

Menggunakan teorem (a.Yo.p.) yang menyatakan bahawa sudut alternatif dalaman antara paralel yang dipotong oleh secant menentukan sudut yang sama, kita dapat menetapkan yang berikut:

α₁ = γ₁, α2 = γ2, δ₁ = Β₁ dan Δ2 = β2. (*)

Sebaliknya, sebagai sisi bersebelahan rombus adalah panjang yang sama, empat segitiga isosceles ditentukan:

DAB, BCD, CDA dan ABC

Sekarang teorem segitiga (isosceles) dipanggil bahawa menyatakan bahawa sudut bersebelahan dengan pangkalan adalah ukuran yang sama, di mana ia menyimpulkan bahawa:

δ₁ = β2, Δ2 = β₁, α2 = γ₁ dan α₁ = γ2 (**)

Jika hubungan (*) dan (**) digabungkan, persamaan sudut seterusnya dicapai:

α₁ = α2 = γ₁ = γ₁ Di satu pihak dan β₁ = Β2 = δ₁ = Δ2 untuk yang lain. 

Mengingat teorem segitiga yang sama yang menegaskan bahawa dua segitiga dengan sisi yang sama antara dua sudut yang sama adalah sama adalah:

Aod = aob dan akibatnya juga sudut ∡AOD = ∡AOB.

Maka ∡AOD + ∡AOB = 180º, tetapi sebagai kedua -dua sudut adalah ukuran yang sama, 2 ∡AOD = 180º yang menunjukkan bahawa ∡AOD = 90º.

Iaitu, secara geometri menunjukkan bahawa pepenjuru rombus dipotong pada sudut tepat.

Latihan diselesaikan

- Latihan 1

Menunjukkan bahawa dalam trapezoid segi empat tepat, sudut bukan EG adalah tambahan.

Penyelesaian

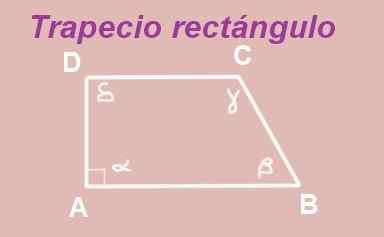Rajah 13. Trapeze Rectangle. Sumber: f. Zapata.

ABCD Trapezoid dibina dengan pangkalan AB dan DC selari. Sudut dalaman puncak A lurus (langkah 90º), jadi anda mempunyai trapezoid segi empat tepat.

Sudut α dan δ adalah sudut dalaman antara dua selari AB dan DC selari, oleh itu ia adalah sama, iaitu δ = α = 90º. 

Sebaliknya, telah ditunjukkan bahawa jumlah sudut dalaman kuadrilateral menambah 360º, iaitu:

α + β + γ + δ = 90º + β + 90º + δ = 360º.

Yang di atas membawa kepada:

 β + δ = 180º

Mengesahkan apa yang ingin ditunjukkan bahawa sudut β dan δ adalah tambahan.

- Latihan 2

Parallelogram ABCD mempunyai ab = 2 cm dan ad = 1 cm, di samping sudut buruk ialah 30º. Tentukan kawasan selaras yang dikatakan dan panjang dua pepenjuru.

Penyelesaian

Kawasan paralelogram adalah hasil panjang pangkalannya dengan ketinggian. Dalam kes ini, panjang segmen b = ab = 2 cm akan diambil sebagai asas, sisi lain mempunyai panjang a = ad = 1 cm dan ketinggian h akan dikira seperti berikut:

H = ad * dosa (30º) = 1 cm * (1/2) = ½ cm.

Kemudian: kawasan = b * h = 2 cm * ½ cm = 1 cm².

Rujukan

1. C. Dan. Ke. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universiti Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Kumpulan Editorial Patria.
3. Dibebaskan, k. (2007). Cari poligon. Syarikat Pendidikan Benchmark.
4. Hendrik, v. (2013). Poligon umum. Birkhäuser.
5. Iger. (s.F.). Matematik semester pertama Tacaná. Iger.
6. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematik: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
8. Patiño, m. (2006). Matematik 5. Progreso editorial.
9. Wikipedia. Quadrilaterals. Pulih dari: Adakah.Wikipedia.com