Berapa banyak paksi simetri yang ada di bulatan?

The Paksi simetri bulatan Mereka tidak terhingga. Paksi ini adalah yang membahagikan sebarang bentuk geometri menjadi dua bahagian yang sama. Dan bulatan terdiri daripada semua titik yang jaraknya ke titik tetap kurang dari atau sama dengan nilai "r" tertentu.

Titik tetap yang disebutkan di atas dipanggil pusat, dan nilai "r" dipanggil radio. Radio adalah jarak terbesar antara titik dalam bulatan dan pusat.

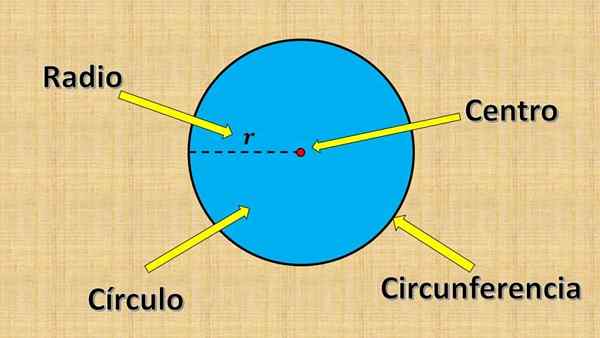
Sebaliknya, mana -mana segmen baris yang hujungnya berada di pinggir bulatan (lilitan) dan yang melewati pusat dipanggil diameter. Ukurannya selalu sama dengan dua kali radio.

Bulatan dan lilitan

Jangan mengelirukan bulatan dengan lilitan. Lingkaran hanya merujuk kepada titik -titik yang berada di jarak "r" pusat; iaitu, hanya tepi bulatan.

Walau bagaimanapun, apabila mencari paksi simetri, tidak peduli jika anda bekerja dengan lilitan atau dengan bulatan.

Apakah paksi simetri?

Paksi simetri adalah garis yang membahagikan angka geometri tertentu menjadi dua bahagian yang sama. Dengan kata lain, paksi simetri bertindak sebagai cermin.

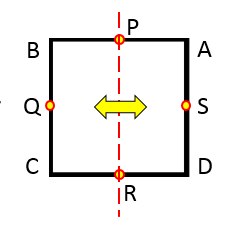Dalam imej sebelumnya, dapat dilihat bahawa garis menegak yang melewati pusat sisi bertentangan persegi adalah paksi simetri yang sama.

Paksi simetri bulatan

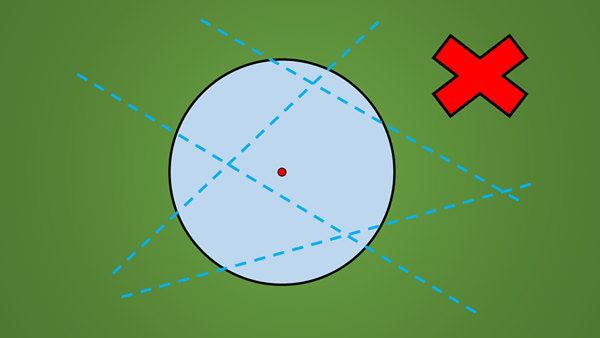
Sekiranya mana -mana bulatan diperhatikan, tanpa mengira jejarinya, dapat dilihat bahawa tidak setiap lurus yang melintasi ia adalah paksi simetri.

Sebagai contoh, tiada garis yang ditarik dalam imej berikut adalah paksi simetri.

Cara mudah untuk memeriksa sama ada garis adalah paksi simetri atau tidak, adalah dengan tegas mencerminkan angka geometri di seberang garis.

Sekiranya refleksi tidak sesuai dengan angka asal, maka kata garis bukan paksi simetri. Dalam imej berikut teknik ini digambarkan.

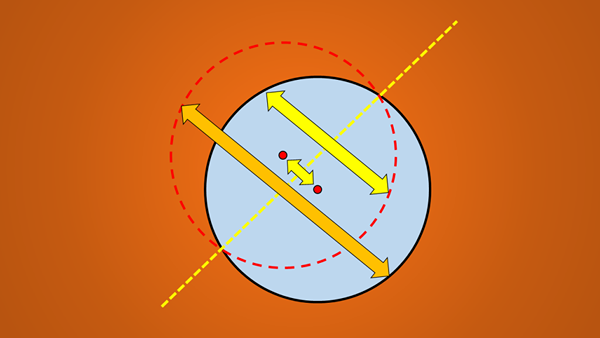
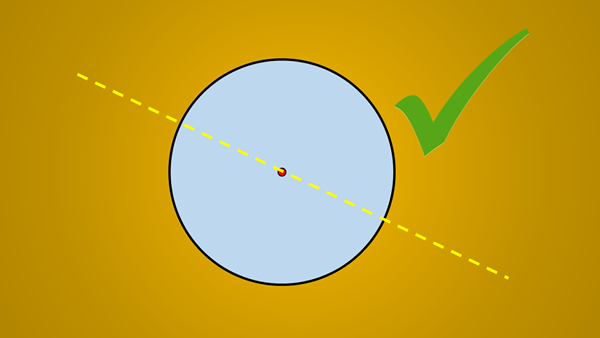
Tetapi jika imej berikut dipertimbangkan, adalah terkenal bahawa garis yang ditarik adalah paksi simetri bulatan.

Persoalannya ialah: Adakah terdapat lebih banyak paksi simetri? Jawapannya ya. Sekiranya garis 45 ° ini diputar dalam pengertian anti -horari, garis yang diperoleh juga adalah paksi simetri bulatan.

Perkara yang sama berlaku jika 90 °, 30 °, ke -8 dan, secara umum, bilangan darjah.

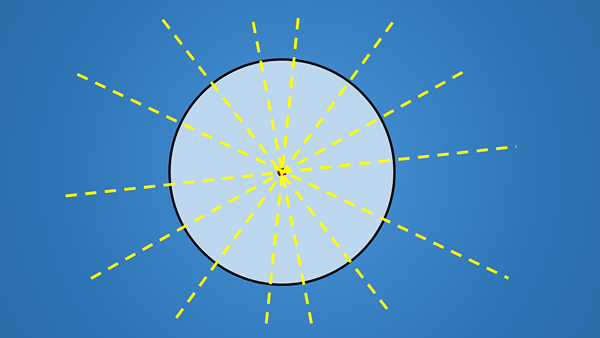
Perkara penting mengenai baris ini bukanlah kecenderungan yang mereka ada, tetapi mereka semua melewati pusat bulatan. Oleh itu, sebarang garis yang mengandungi diameter bulatan adalah paksi simetri.

Jadi, kerana bulatan mempunyai jumlah diameter yang tidak terhingga, maka ia mempunyai jumlah paksi simetri tak terhingga.

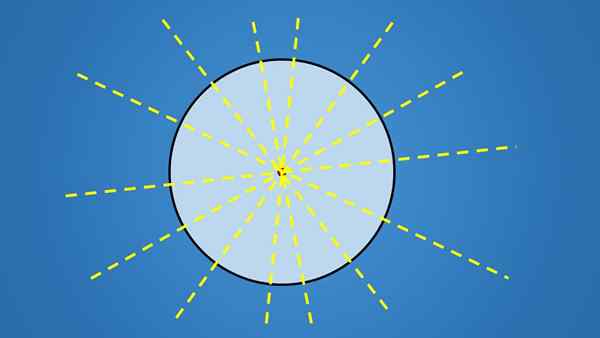
Tokoh geometrik lain, seperti segitiga, segi empat, pentagon, segi enam atau poligon lain, mempunyai jumlah paksi simetri terhingga.

Sebab mengapa bulatan mempunyai jumlah paksi simetri yang tidak terhingga adalah bahawa ia tidak mempunyai sisi.